The Binary GCD algorithm or Stein's algorithm, is an algorithm that calculates two non-negative integer's largest common divisor by using simpler arithmetic operations than the standard euclidean algorithm and it reinstates division by numerical shifts, comparisons, and subtraction operations.

• Examples: Input: x = 12,y = 72
  Output : 12
• Input: x = 33, y = 34
  Output: 1

Algorithm

The Binary GCD Algorithm for calculating GCD of two numbers x and y can be given as follows:

1. If both x and y are 0, gcd is zero gcd(0, 0) = 0.
2. gcd(x, 0) = x and gcd(0, y) = y because everything divides 0.
3. If x and y are both even, gcd(x, y) = 2*gcd(x/2, y/2) because 2 is a common divisor. Multiplication with 2 can be done with bitwise shift operator.
4. If x is even and y is odd, gcd(x, y) = gcd(x/2, y).
5. On similar lines, if x is odd and y is even, then
6. gcd(x, y) = gcd(x, y/2). It is because 2 is not a common divisor.
7. If both x and y are odd, then gcd(x, y) = gcd(|x-y|/2, y)
8. Repeat steps 3–5 until x = y, or until x = 0. In either case, the GCD is power(2, k) * y, where power(2, k) is 2 raise to the power of k and k is the number of common factors of 2 found in step 2.

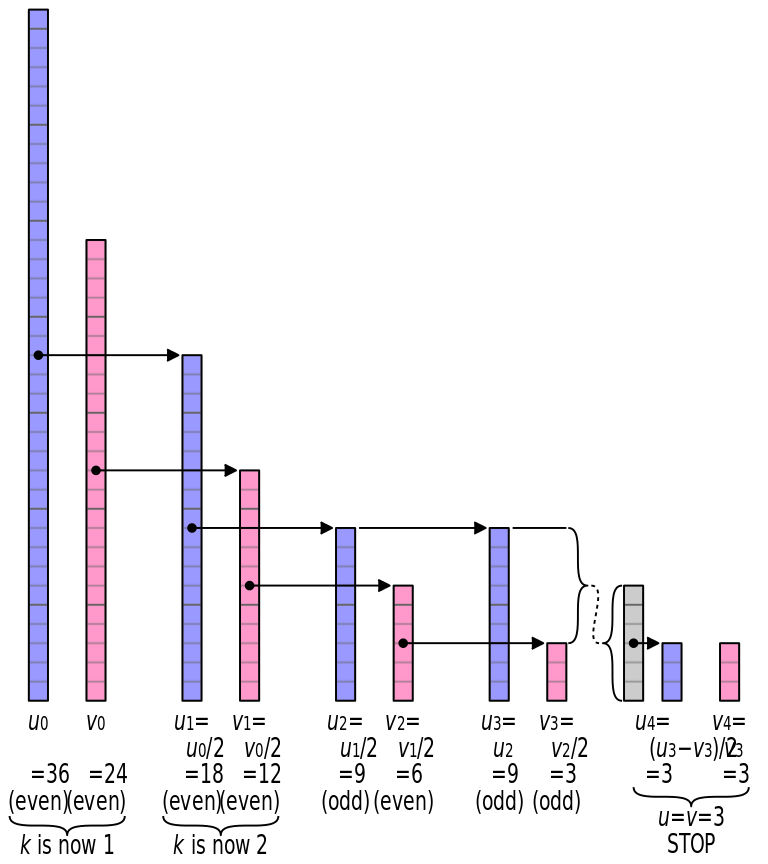
The above image shows the binary GCD algorithm to find the greatest common divisor (GCD) of 36 and 24 through a graphical representation. Thus, the GCD is 2² × 3 = 12

PseudoCode

Following is the pseudocode of the above algorithm:

function binaryGCD(int u, int v) {
    //simple termination cases
    if v equals 0 : return u;
    if u equals 0 : return v;

// If u and v are both even, then gcd(u, v) = 2·gcd(u/2, v/2), because 2 is a common divisor
    if ((u is even) and (v is even)){
        return binaryGCD(u >> 1, v >> 1) << 1;
    }

// If u is even and v is odd, then gcd(u, v) = gcd(u/2, v), because 2 is not a common divisor
    else if (u is even){
        return binaryGCD(u >> 1, v);
    }

// If u is odd and v is even, then gcd(u, v) = gcd(u, v/2)
    else if (v is even){
        return binaryGCD(u, v >> 1);
    }

// If u and v are both odd, and u ≥ v, then gcd(u, v) = gcd((u − v)/2, v)
    else if (u >= v){
        return binaryGCD((u-v) >> 1, v);
    }

// If both are odd and u < v, then gcd(u, v) = gcd((v − u)/2, u)
    else{
        return binaryGCD(u, (v-u) >> 1);
    }
}

Detailed Example

Another Example, finding GCD of 12 and 18

gcd ( 12 , 18 ) = 2 * gcd ( 6 , 9 )
gcd ( 6 , 9 ) = gcd ( 3 , 9 )
gcd ( 3 , 9 ) = gcd ( 6 , 3 )
gcd ( 6 , 3 ) = gcd ( 3 , 3 )

Hence the result is 2 * 3 = 6

Complexity

• Worst case time complexity: Θ((logN)2)

The algorithm requires the worst-case time of O((logN)²),while each step decreases one of the operands by a minimum factor of 2, the subtract and shift operations , for huge entities, take linear time (though they are still very quick in practice, requiring around a single operation per word ).

logN denotes the number of digits in a number N. This arises from the factor a number reduces by a factor of 2 where 2 is the base of the logarithm.

Implementation

Implementation of the above algorithm in C++

// Iterative Approach 
#include <bits/stdc++.h> 
using namespace std; 

//GCD Function
int gcd(int x, int y) 
{ 

    if (x == 0) 
        return y; 
    if (y == 0) 
        return x; 

    /*Finding K, where K is the 
    greatest power of 2 
    that divides both a and b. */
    int k; 
    for (k = 0; ((x | y) && 1) == 0; ++k) 
    { 
        x >>= 1; 
        y >>= 1; 
    } 

    /* Dividing x by 2 until x becomes odd */
    while ((x > 1) == 0) 
        x >>= 1; 

    /* From here on, 'x' is always odd. */
    do { 
        /* If y is even, remove all factor of 2 in y */
        while ((y > 1) == 0) 
            y >>= 1; 

        // Now x and y are both odd
        if (x > y) 
            swap(x, y); // Swap u and v. 

        x = (y - a); 
    } while (y != 0); 


    return x << k; 
} 

// Driver code 
int main() 
{ 
    int x = 72, b = 12; 
    cout<<"Gcd of given numbers is "<< gcd(x, y)); 
    return 0; 
} 

Recursive Implementation of the above algorithm

// Recursive program 
#include <bits/stdc++.h> 
using namespace std; 

// Function to implement the  
// Stein's Algorithm 
int gcd(int x, int y) 
{ 
      if (x == y) 
         return x; 
      if (x == 0) 
         return y; 
      if (y == 0) 
         return x; 

    // look for factors of 2 
    if (~x & 1) // x is even 
    { 
        if (y & 1) // y is odd 
            return gcd(x >> 1, y); 
        else      // both x and y are even 
            return gcd(x >> 1, y >> 1) << 1; 
    } 

    if (~y & 1) // x is odd, y is even 
        return gcd(x, y >> 1); 

    // reduce larger number 
    if (x > y) 
        return gcd((x - y) >> 1, y); 

    return gcd((y - x) >> 1, x); 
} 

// Driver code 
int main() 
{ 
    int a = 34, b = 17; 
    cout<<"Gcd of given numbers is"<<gcd(a, b)); 
    return 0; 
}

Efficiency

It has been shown that , binary GCD algorithm can be nearly 60 per cent more cost-effective (in comparison to the number of bit operations) than the Euclidean method on an average. Although this approach moderately outshines the regular Euclidean algorithm in real implementations, its asymptotic efficiency is the same and the binary GCD algorithm is considerably more productive in real implementations.

Applications

Some of the applications of Stein's Algorithm are :

• It is optimised for use in computing
• Computers that use the .NET framework may use this for some improvement in efficiency

For more such interesting algorithms, have a look at the algorithms section of Opengenus IQ below:

Learn more about other Algorithms

With this article at OpenGenus, you must have the complete idea of Binary GCD Algorithm. Enjoy.