Binary Heap

Binary heap is a complete Binary tree structured as a heap data structure. Binary heaps are common way of implementing priority queues.

Binary heaps are also commonly employed in the heapsort sorting algorithm, which is an in-place algorithm because binary heaps can be implemented as an implicit data structure, storing keys in an array and using their relative positions within that array to represent child-parent relationships.

Algorithm	Average	Worst Case
Space	O(n)	O(n)
Search	O(n)	O(n)
Insert	O(1)	O(log n)
Delete	O(log n)	O(log n)
Peek	O(1)	O(1)

Pre-requisites:

• Binary Tree
• Min and Max Heap

Properties of Binary Heap

A Binary tree is a Binary heap data structure when following two properties are satisfied:

1. A binary tree is a complete Binary tree i.e. all the levels of tree are commpletely filled except the last level. If the last level is not filled, they are filled from left to right.
2. The key stored in each node is either less than or equal to (<=) or greater than equal to (>=) the parent node of the key.

There are two ways to implement heap data structures.

1. Max-Heaps-
   Heaps where the parent node is greater than equal to (>=) its children are called max heaps. This property is applied to every node of the tree.
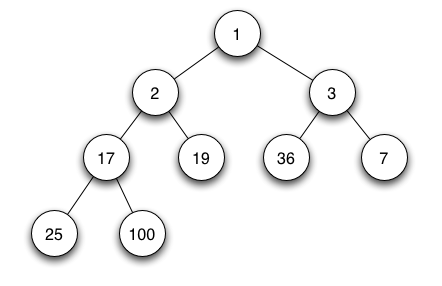
   example-
   

2. Min-Heaps-
   Heaps where the parent node is less than or equal to (<=) its children are called Min-Heaps. Again, this property is applied to all the nodes in the tree.
   

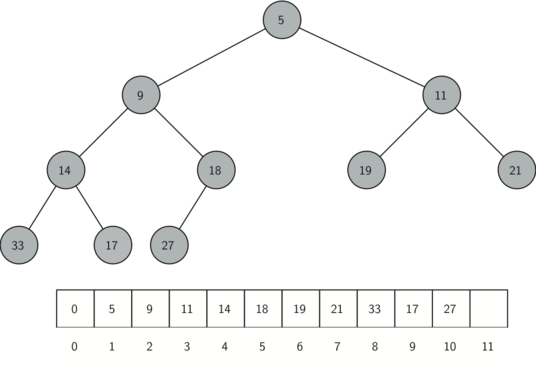
An array representation of Binary heap.
We can see that the nodes are represented in a level order in an array.
For implementing binary heap, we must be able to find relations in a binary tree structure and its array representation.
The root node has 2 children-
index 1 has indexes 2 and 3 as children.(5 has 9 and 11 as children)
Index 2 has 4 and 5 as its hildren. (9 has 15 and 18)
We can see a pattern emerging here. Mathematical way fo representing children and parent of a node if node[i] is our key then.
Left child of node[i] is node[i * 2] and
Right child is node[i * 2 + 1]
and Parent of node[i] will be node[i // 2].
"//" in python returns an integer which is less than or equal to actual divison.
For eg node 9 in our tree-:
Node 9 has index 2, so its left child would be 2 * 2 i.e index 4 which is 14 ! and its right child is 2 * 2 + 1 = 5
node[5] = 18.
Parent of 9 = node[2] => node[2 // 2] = node[1] = 5
Done with some study pf array and binary heap, we are ready to look how a Min-Heap is implemented.

Implementation of Min-Heap

Let us define what parent, left and right children could be.
As we have seen parent is i // 2
left child is i * 2 and right child is i * 2 + 1

Defining a class of BinaryHeap. Constructors will initilize a list and an attributre currentSize which keeps track of current size of the heap. Empty Binary heap has single zero as its first element, as it makes our simple integer divisions easier. 0 is never used in our code.

In case if elements are filled in an array from 0 index then left child = i * 2
right child = i * 2 + 1

class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0
        
    def parent(self, i):   #parent node
        return (i - 1)//2   
 
    def left(self, i):     #left child
        return 2*i + 1
 
    def right(self, i):    #right child
        return 2*i + 2         

Insertion in Binary Heap

We can simply append the new element at the end of our list using python function called by the same name. But appending at the end violates the properties of a binary heap for that we should define a function which could restore the min-heap property by comparing the newly added element with its parent. If parent is greater than our new node then swap these 2 nodes, repeat this step till the root node is the smallest node.

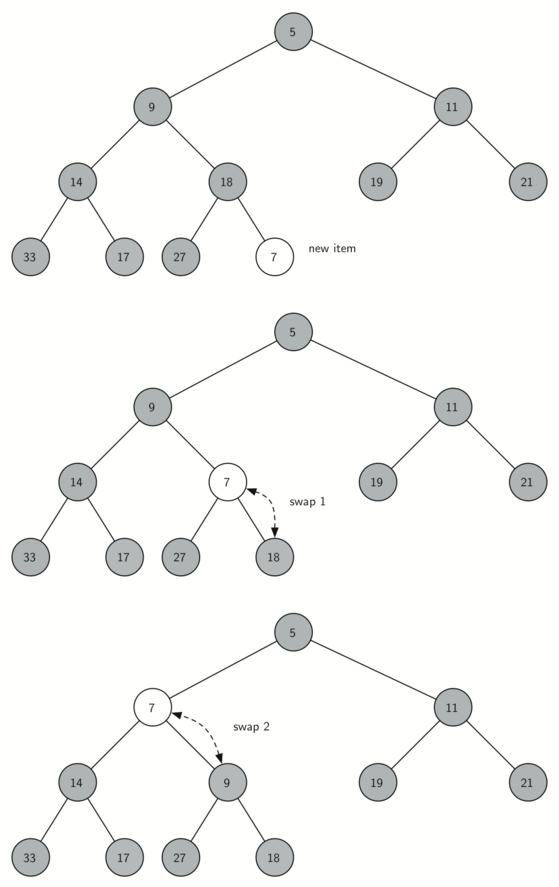
Pseudocode

1. Add the element to the bottom level of the heap at the most left.
2. Compare the node with its parent, if parent_node <= New_node. then stop.
3. If not then swap the element with its parent and return to the previous step.

Let's define another function for step no 3.

def Up
We named it up because this function is percolating up from the bottom. We are checking the conditions with parents that is gradually going up the tree

def Up(self,i):
    while i // 2 > 0:      #i//2 returns parent node index
      if self.heapList[i] < self.heapList[parent(self, i)]:
      ## swap using third variable
         tmp = self.heapList[i // 2]
         self.heapList[i // 2] = self.heapList[i]
         self.heapList[i] = tmp
      i = i // 2         update i

while i // 2 is just a condition to check if the parent node exist or not. Condition i false if i // 2 = 0.
Then we compare the new element with its parent node by calling parent function returning index of parent node.
Using basic Swapping with an extra variable method we will swap the elements if condition is true.
Then we update the value of i to its parent.

def insert(self,k):
    self.heapList.append(k)  #adding element at the last
    #increase current size of our list
    self.currentSize = self.currentSize + 1     
    self.Up(self.currentSize)

This was insertion.

Deleting a root in Binary Heap

Deletion in a binary heap tree can be done by swapping the last node with the root node to be removed and then performing some operations to restore the property of our Min heap tree.

For eg if we want to delete root node of our tree.

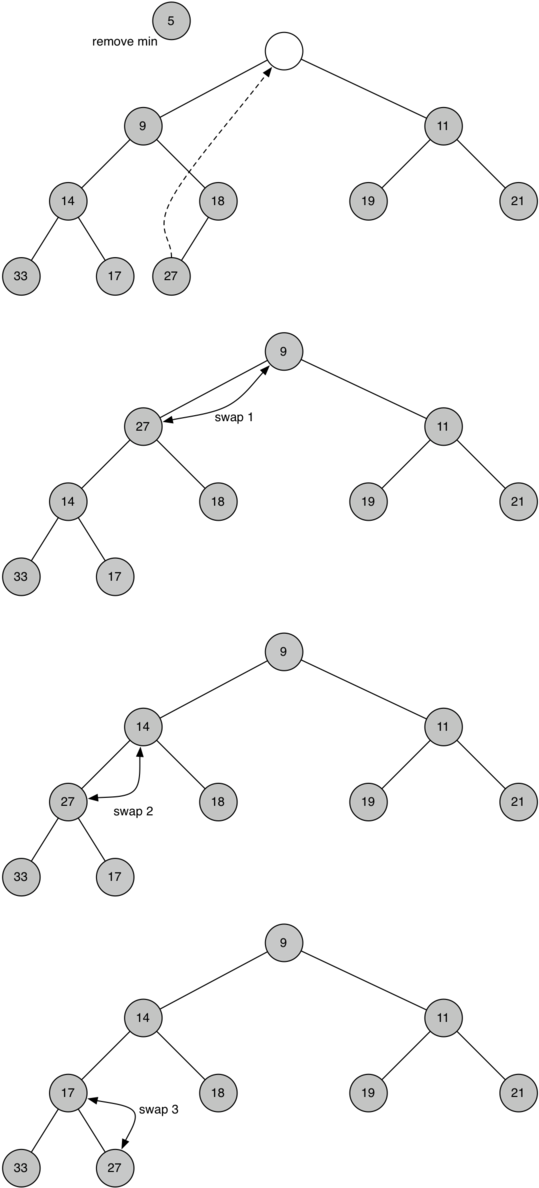
For deleting 5 from our tree we bring the last node at the root and then checking if the root node is less than its left child, if its less condition is satisfied. If not then swap with its child and perform this till its a Binary min heap tree.

Pseudocode

1. Replace the root node with last element of list or the left most node.
2. Compare the new root node with its children, if they are in sorted order. stop
3. if not, then swap one of the element with its parent and return to the previous step. Swap with its smaller child in min heap

Here, we have to find minimum element among the two children, and then percolating down to check conditions and swapping.
We will define 2 new functions down, minChild, Down
Down function is just the opposite of Up function where we are percolating Down instead of Up, checking the conditions with children.

def Down(self,i):
    #checking if node is a leaf node, i*2 is parent node index of i
    while (i * 2) <= self.currentSize: 
        mc = self.minChild(i)
        if self.heapList[i] > self.heapList[mc]:
        #Swap if parent > minChild
            tmp = self.heapList[i]
            self.heapList[i] = self.heapList[mc]
            self.heapList[mc] = tmp
        i = mc

def minChild(self,i):
    #check if children exist, if doesnt return leaf node
    if i * 2 + 1 > self.currentSize:
        return i * 2
    else:
        if self.heapList[i*2] < self.heapList[i*2+1]:
            return i * 2
        else:
            return i * 2 + 1

We are checking if children exist. If it does then call minChild function to return the minimum element among the 2.

check if parent > minChild, if it does then swap with minChild. Repeat this process again and again till it is a binary heap tree.
minchild first check if left < right return left child and vice a versa.

def delMin(self):
    retval = self.heapList[1]
    self.heapList[1] = self.heapList[self.currentSize]
    self.currentSize = self.currentSize - 1
    self.heapList.pop()   #removing last empty key
    self.percDown(1)
    return retval

Build Binary Heap

We will now look at how to construct entire Min-Heap tree from the given list of keys.
Following figure shows the steps for building the tree.

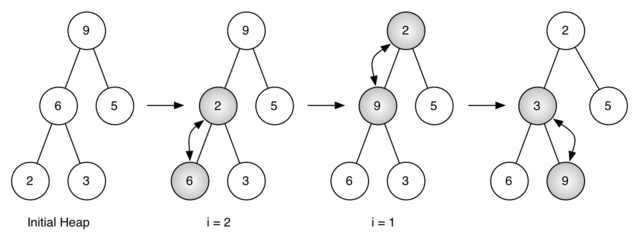
Array representation of steps involved in build

i = 2  [0, 9, 5, 6, 2, 3]
i = 1  [0, 9, 2, 6, 5, 3]
i = 0  [0, 2, 3, 6, 5, 9]

We start from the middle and work our way back toward the root node using Down method. This method will ensure that the largest node is pushed as low as it can go, completing the properties of a binary Min-Heap tree.
In our case, we start from the middle node 6, checking which the minimum among 2 and 3. If 6 > 2 we swap to bring 2 in place of 6. Now, i is decremented by 1, now comparing 9 with 2 and swapping to ensure 9 is at the lower most level.

Pseudocde

1. lenght of list // 2.
2. Perform Down from index i//2, till we reach at the bottom.
3. Decrease i, repeat previous step.

def buildHeap(self,alist):
    #Middle element of our array
    i = len(alist) // 2
    self.currentSize = len(alist)
    self.heapList = [0] + alist[:]
    while (i > 0):
        self.percDown(i)
        i = i - 1

Entire code for Min-Heap

class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0


    def percUp(self,i):
        while i // 2 > 0:
          if self.heapList[i] < self.heapList[i // 2]:
             tmp = self.heapList[i // 2]
             self.heapList[i // 2] = self.heapList[i]
             self.heapList[i] = tmp
          i = i // 2

    def insert(self,k):
      self.heapList.append(k)
      self.currentSize = self.currentSize + 1
      self.percUp(self.currentSize)

    def percDown(self,i):
      while (i * 2) <= self.currentSize:
          mc = self.minChild(i)
          if self.heapList[i] > self.heapList[mc]:
              tmp = self.heapList[i]
              self.heapList[i] = self.heapList[mc]
              self.heapList[mc] = tmp
          i = mc

    def minChild(self,i):
      if i * 2 + 1 > self.currentSize:
          return i * 2
      else:
          if self.heapList[i*2] < self.heapList[i*2+1]:
              return i * 2
          else:
              return i * 2 + 1

    def delMin(self):
      retval = self.heapList[1]
      self.heapList[1] = self.heapList[self.currentSize]
      self.currentSize = self.currentSize - 1
      self.heapList.pop()
      self.percDown(1)
      return retval

    def buildHeap(self,alist):
      i = len(alist) // 2
      self.currentSize = len(alist)
      self.heapList = [0] + alist[:]
      while (i > 0):
          self.percDown(i)
          i = i - 1

bh = BinHeap()
bh.buildHeap([9,5,6,2,3])

print(bh.delMin())
print(bh.delMin())
print(bh.delMin())
print(bh.delMin())
print(bh.delMin())

With this article at OpenGenus, you must have the complete idea of Binary Heap.