
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will discuss about the Worst Case Time Complexity about 'Quick-Sort' algorithm along with the complete time complexity analysis of the worst case.
Content:
- Introduction
- How it works
- When does the worst case occur
- Time Complexity annalysis with Example
- Implementation of Quicksort
- How to avoid worst-case
In short, Worst Case of Quick Sort is when elements are sorted, reverse sorted or all elements are same. Time Complexity of Worst Case is O(N2).
Introduction
Quicksort is very common and most efficiently used sorting algorithm.It is a divide-and-conquer algorithm.As this algorithm recursively call the function so does not use any extra space for sorting input data still it uses stack of size (log(n) to n).Log(n) in best case and n in worst case.
How it works
Quicksort is a fast algorithm that works by dividing a large array of data into smaller sub parts.An element is selected as pivot element and partitions are done around that pivot. There are different ways for selecting a pivot:
- Pick first element as pivot.
- Pick last element as pivot.
- Pick random element as pivot.
- Pick median as pivot.
- Choose a pivot element from array
- Iterate through every element in the array except the pivot and make sure that pivot element is sorted
- Now return the pivot index
- Once partitioned, now make 2 calls on quicksort
One from start to pivot-1
Other from pivot+1 to end
Pseduo Code:
partition (array, start, end)
{
// pivot (Element to be placed at right position)
pivot = array[end];
i = (start - 1) // Index of smaller element and indicates the
// right position of pivot found so far
for (j = start; j <= end- 1; j++)
{
// If current element is smaller than the pivot
if (array[j] < pivot)
{
i++; // increment index of smaller element
swap array[i] and array[j]
}
}
swap array[i + 1] and array[end])
return (i + 1)
}
Pseduo Code:
quick_sort(array, start, end)
{
if(start<end)
{
pivot_index = partition(array, start, end);
quick_sort(array, start, pivot_index-1);
quick_sort(array, pivot_index+1, end);
}
}
We got the output as sorted array.
When does the worst case occur for Quick Sort?
As we have seen, pivot plays an important role in the efficiency of the quicksort algorithm.But the efficiency of the algorithm decreases when pivot element divides the array into two sub-array with huge difference in size.
These are three cases when this happens:
- When input array is already sorted
- When the array is reverse sorted
- When all elements of array are same
We will understand each case in detail.
- When input array is already sorted
When array is sorted and we take the left most element as pivot element.
After partitioning around pivot ,we will have two sub-array one with 0 elments and other with n-1.
- When the array is reverse sorted
When array is reverse sorted and we take the right most element as pivot element.
After partitioning around pivot ,again we will have two sub-array one with 0 elments and other with n-1.
- When all elements of array are same
In this case if we take either left most element or the right most element as pivot element,it split the array into one sub-array of size n-1 due to which peformance of this algorithm decreases significantly.
Time Complexity annalysis of Worst Case with Example
- Case 1:When Input array is sorted
Let's take an array=[1,2,3,4,5,6]
Now,
Set the left most element of array as pivot element,and make partition around it, repeat the process.We found that for sorting the pivot element we have to iterate the complete sub-arrays every time.
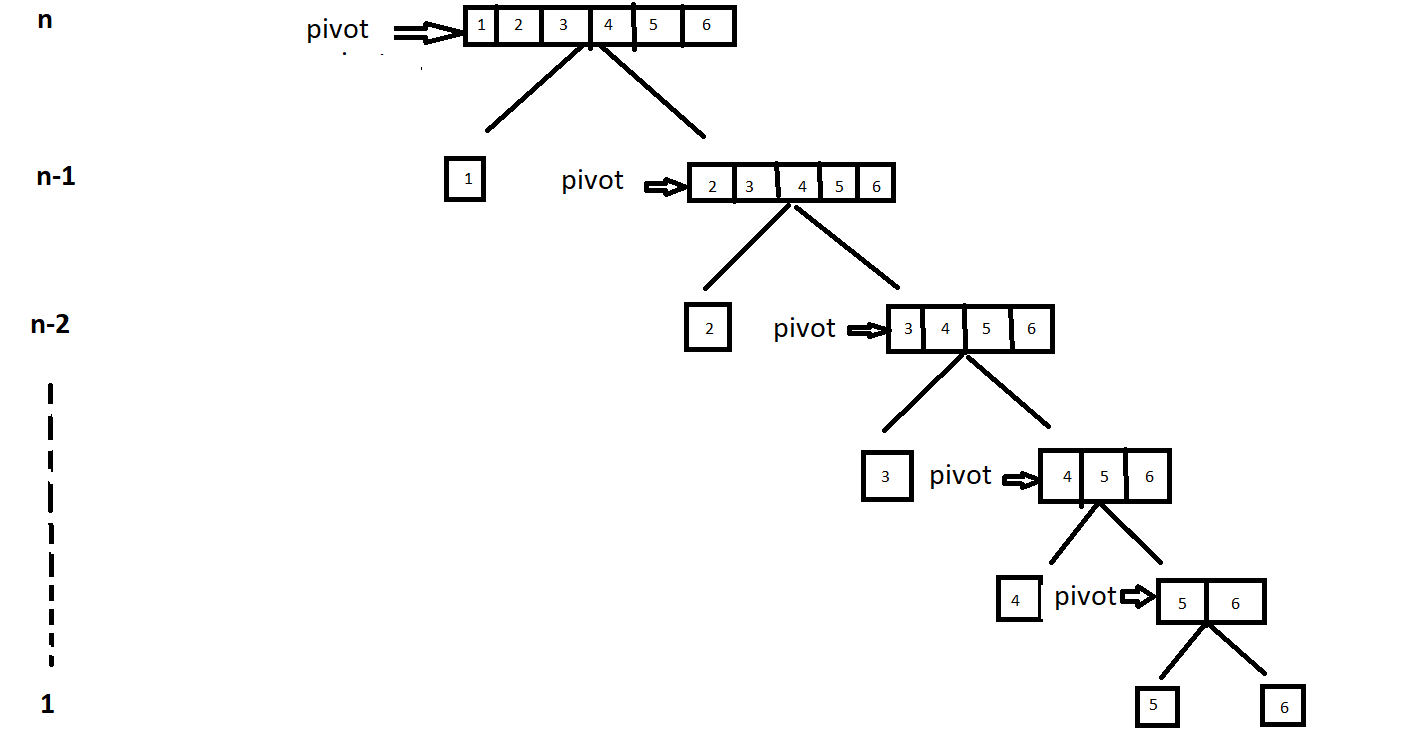
So, time coplexity= n+(n-1)+(n-2)+.......+1
T.C=n(n+1)/2
or,
T.C=O(n^2)
- Case 2:When Input array is reverse sorted
Let's take an array=[6,5,4,3,2,1]
Now,
Set the right most element of array as pivot element ,and make partition around it,repeat the process.We found that for sorting the pivot element we have to iterate the complete sub-arrays every time.
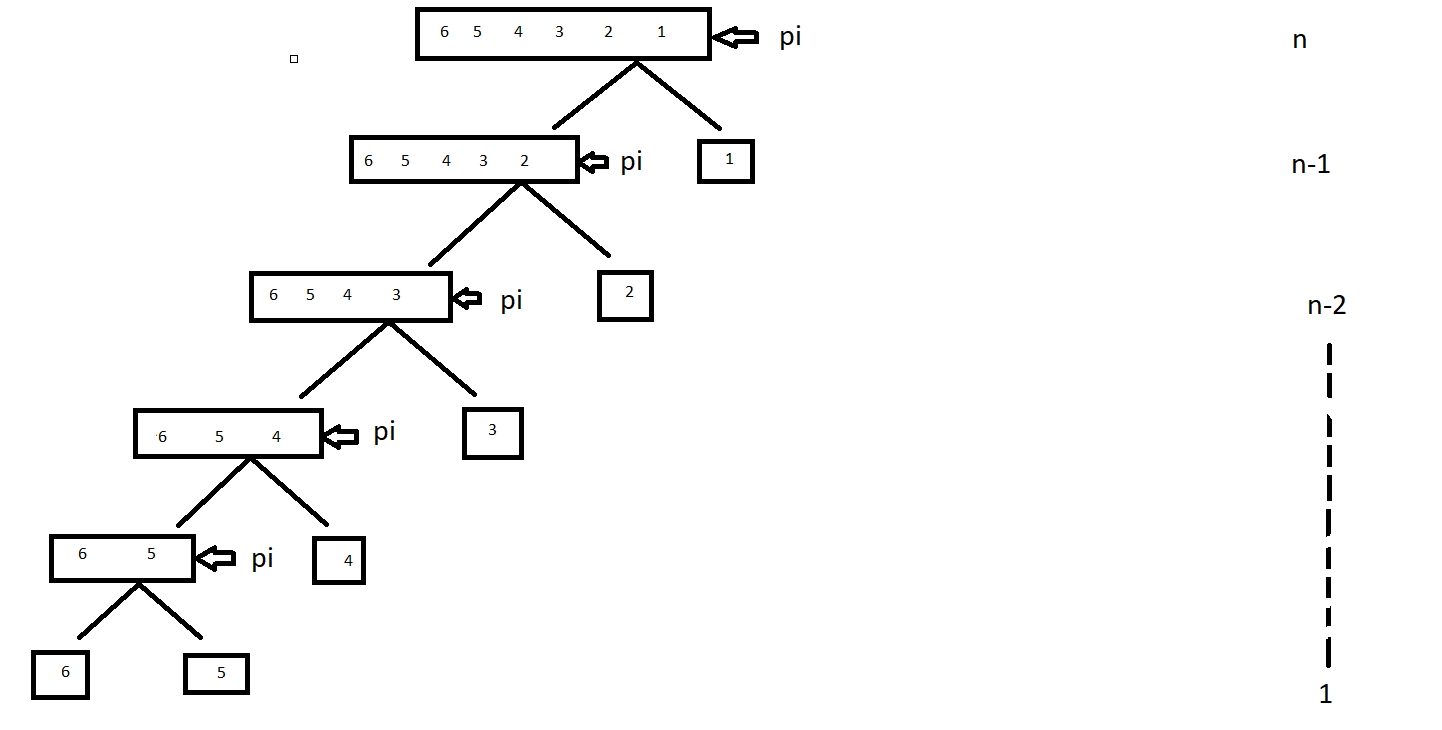
So, time coplexity= n+(n-1)+(n-2)+.......+1
T.C=n(n+1)/2
or,
T.C=O(n^2)
- Case 3:When all elements of array are same
Let's take an array=[2,2,2,2,2,2]
Now,
Set the left most element of array as pivot element,and make partition around it, repeat the process.We found that for sorting the pivot element we have to iterate the complete sub-arrays every time.
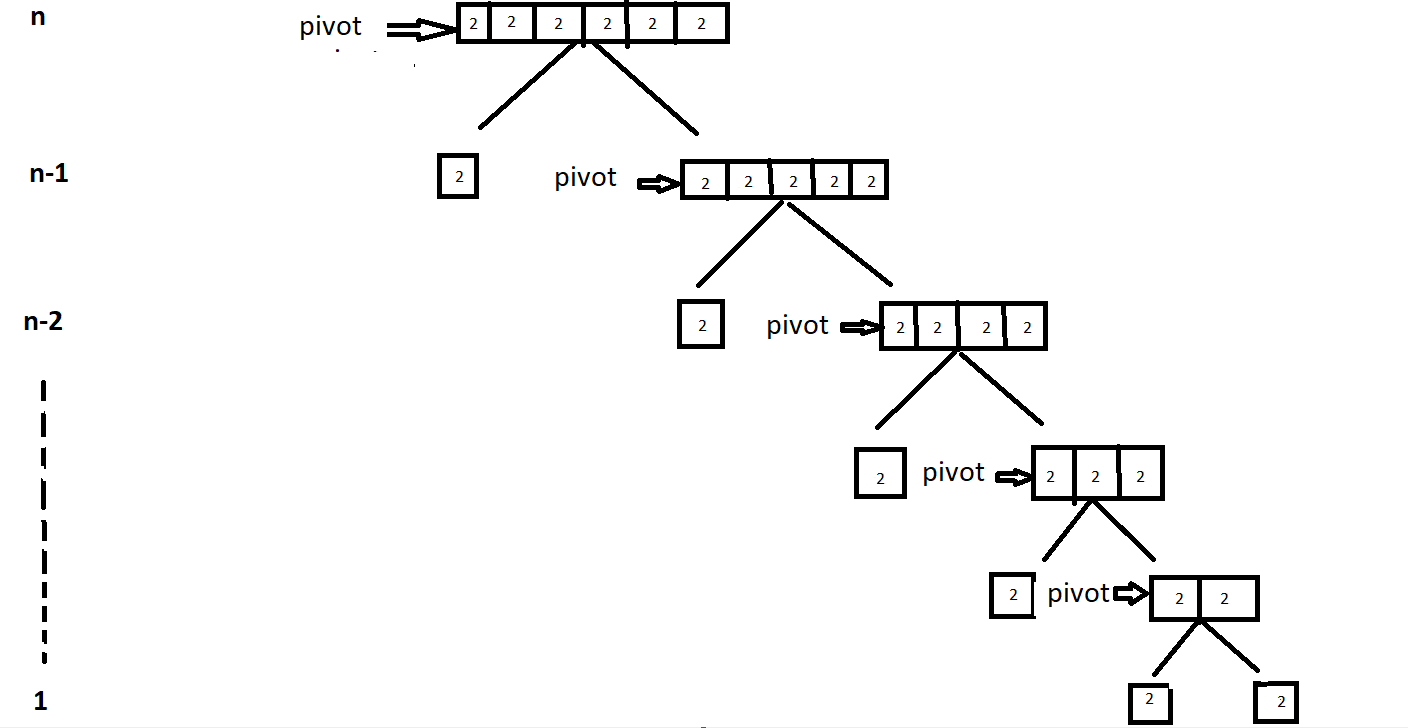
So, time coplexity= n+(n-1)+(n-2)+.......+1
T.C=n(n+1)/2
or,
T.C=O(n^2)
Implementation of Quicksort
#include <bits/stdc++.h>
using namespace std;
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
int partition (int arr[], int low, int high)
{
int pivot = arr[high];
int i = (low - 1); of pivot found so far
for (int j = low; j <= high - 1; j++)
{
if (arr[j] < pivot)
{
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high)
{
if (low < high)
{
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
int main()
{
int arr[] = {3,4,5,6,7};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n - 1);
cout << "Sorted array: \n";
printArray(arr, n);
return 0;
}
How to avoid worst-case in Quick Sort?
We already know selection of pivot element determines the efficiency of algorithm.We can avoid the worst-case in Quicksort by choosing an appropriate pivot element.There are some ways to choose a pivot element:
1.Pick the pivot element from middle of array.
By this way, we can divide the input array into two subarrays of an almost equal number of elements in it.
2.Select the random element as pivot element.
This variant of Quicksort is known as the randomized Quicksort algorithm.
3.Select a pivot element is to take the median of three pivot candidate.
Take the median of left most element ,pivot element and right most element median.
With this article at OpenGenus, you must have the complete idea of Worst Case of Quick Sort.
