Binary step function is one of the most common activation function in neural networks out there. But before we get into it let's take a look at what activation functions and neural networks are.
Table of contents:
- Brief overview of neural networks and activation functions
- What is binary step function?
- Conclusion
Brief overview of neural networks and activation functions
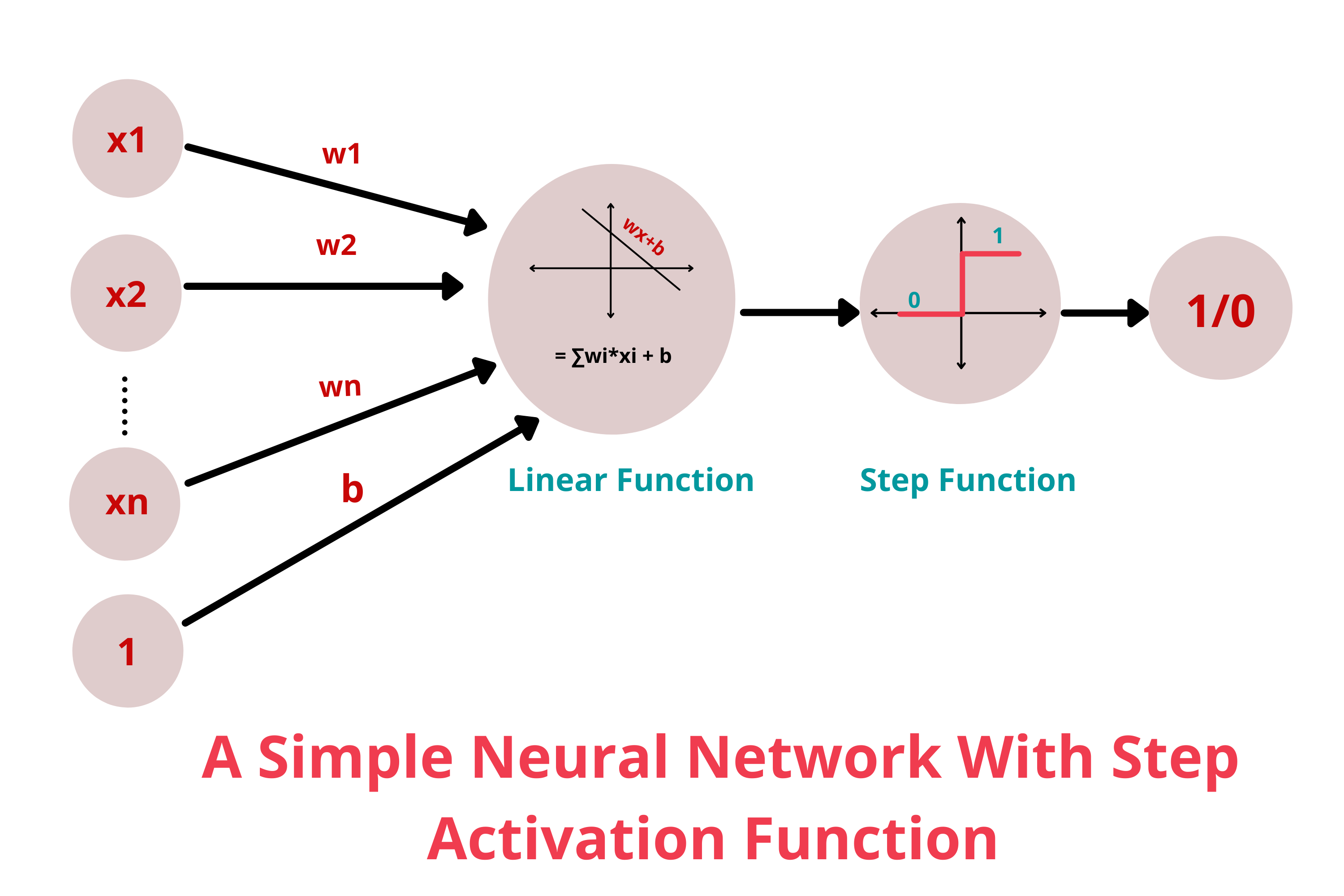
Neural networks are a powerful machine learning mechanism that mimic how the human brain learns. Perceptrons are the basic building blocks of a neural network. A perceptron can be defined as anything that takes multiple inputs and produces one output.
Activation functions are mathematical equations that determine the output of a neural network. They basically decide to deactivate neurons or activate them to get the desired output thus the name, activation functions.
In a neural network, input data points are fed into the neuron. Each neuron has a respective weight which are multiplied by the inputs and added to a staic bias value(unique to each neuron).
x = (weight * input) + bias
This is then passed to an apropriate activation function.
Y = Activation function(∑(weight*input) + bias)
The output achieved will be again fed into the neurons in the next layer and the same process is repeated.
Activation functions can be categorized into three main categories:
- Binary Step Function
- Linear Activation Function
- Non-Linear Activation functions
- Sigmoid function
- tanh function
- ReLU function
to name a few.
What is binary step function?
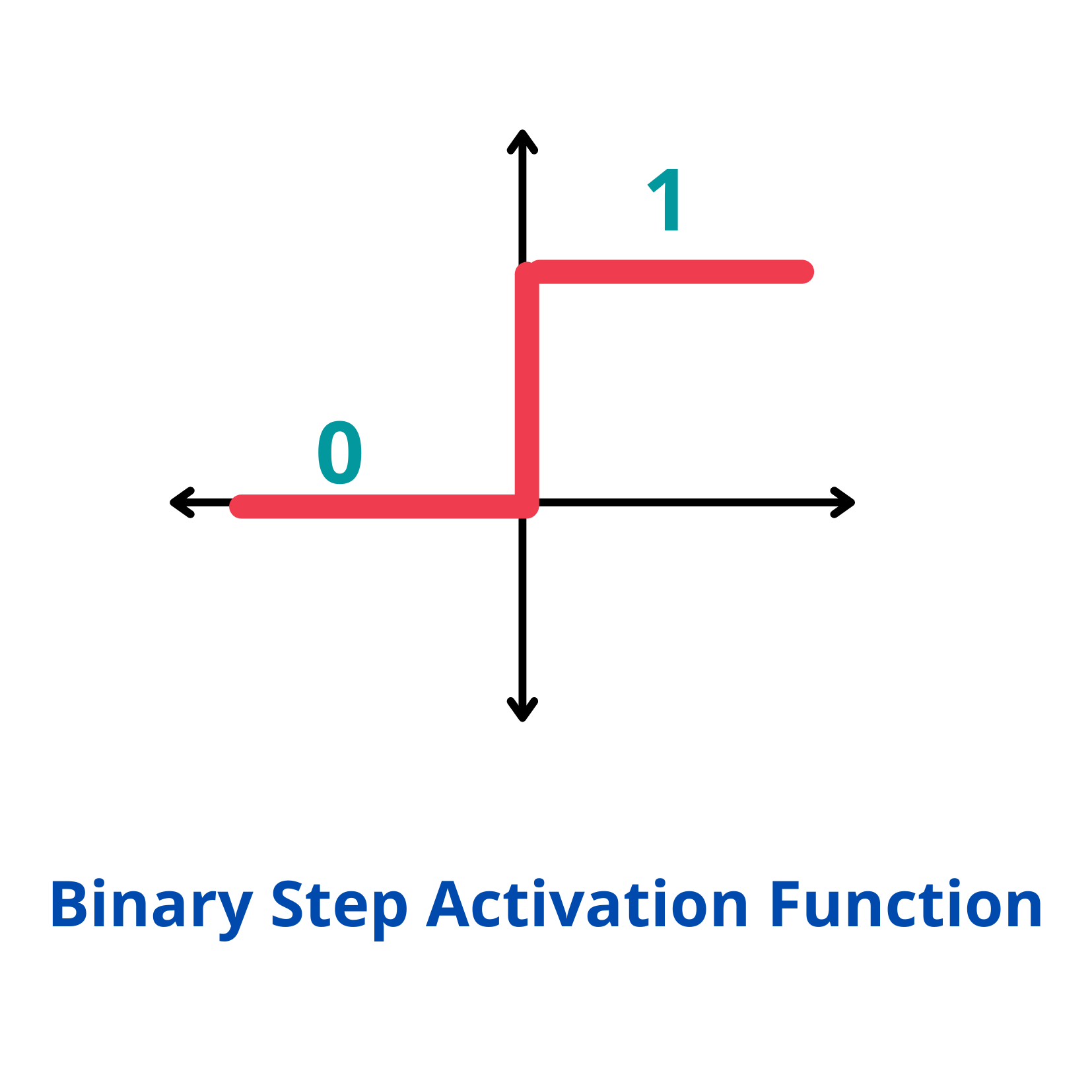
Binary step function is one of the simplest activation functions. The function produces binary output and thus the name binary step funtion. The function produces 1 (or true) when input passes a threshold limit whereas it produces 0 (or false) when input does not pass threshold.
f(x) = 1, x>=0
= 0, x<0
This is the simplest activation function, which can be implemented with a single if-else condition in python
def binary_step(x):
if x<0:
return 0
else:
return 1
binary_step(5), binary_step(-1)
Output :
(5,0)
Step function is commonly used in primitive neural networks without hidden layer.
The binary step function can be used as an activation function while creating a binary classifier. But the function is not really helpful when there are multiple classes to deal with.
Moreover, the gradient of the step function is zero which causes a hindrance in the back propagation process. That is if you calculate the derivative of f(x) with respect to x, it comes out to be 0.
f'(x) = 0, for all x
Conclusion
In this article at OpenGenus, we have discussed about neural networks and activation functions in brief and also about binary step function, its uses and its disadvantages.
