Convert Decimal to Hexadecimal

In this article, we will learn about decimal numbers, hexadecimal numbers and the algorithm to convert decimal to hexadecimal number.

TABLE OF CONTENTS:

1.What is Number System?
2.What are Decimal Numbers?
3.What are Hexadecimal Numbers?
4.Algorithm for Conversion of Decimal to Hexadecimal
5.Program Implementation
6.Example with Detailed Explanation.
7.Example With the table Illustration
8.Examples to Workout.
9.Game Time

Number System

Number system is a system to represent numbers or quantities.We use digits or other symbols to define quantities.It also provides certain arithmetic operations to work on it.

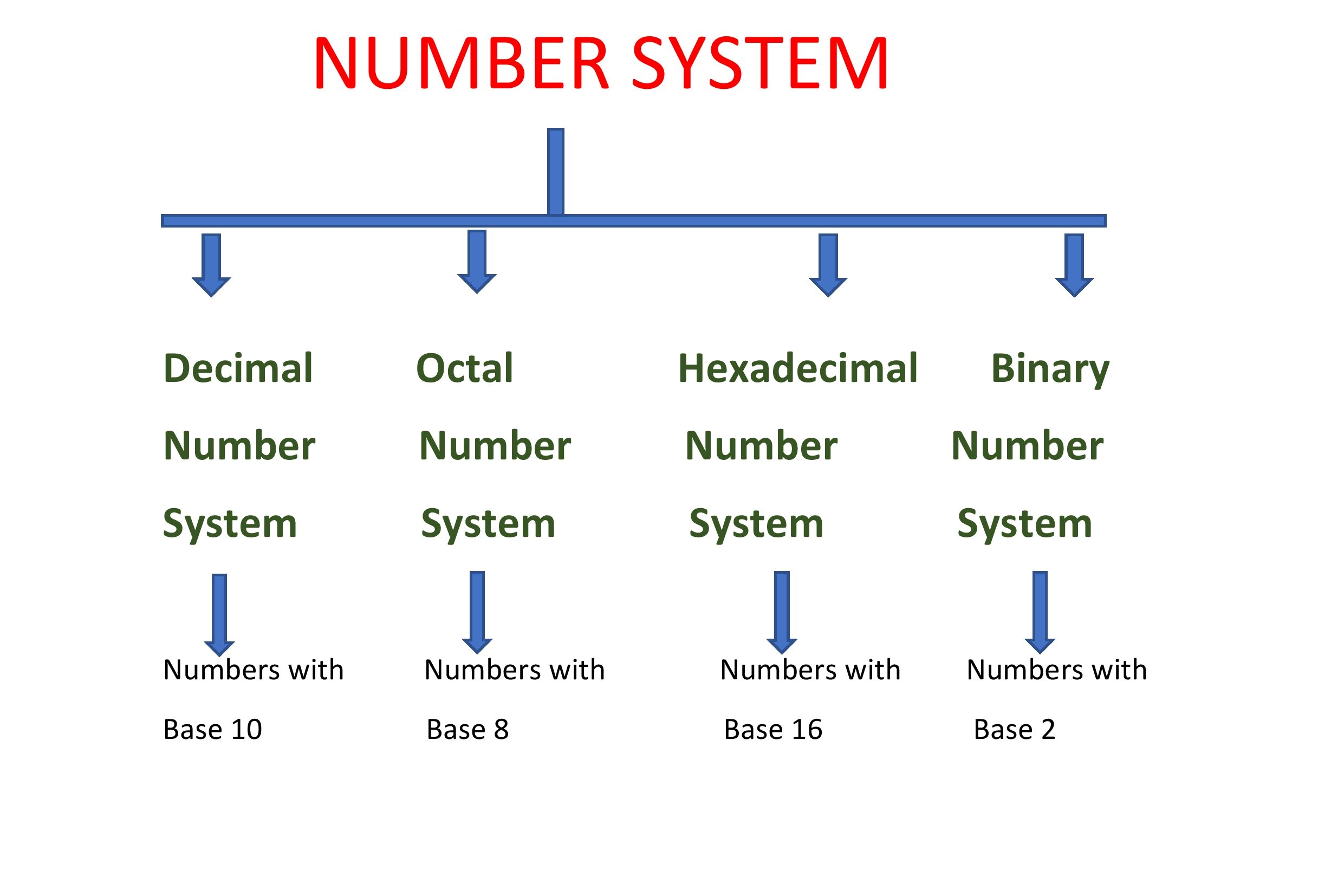
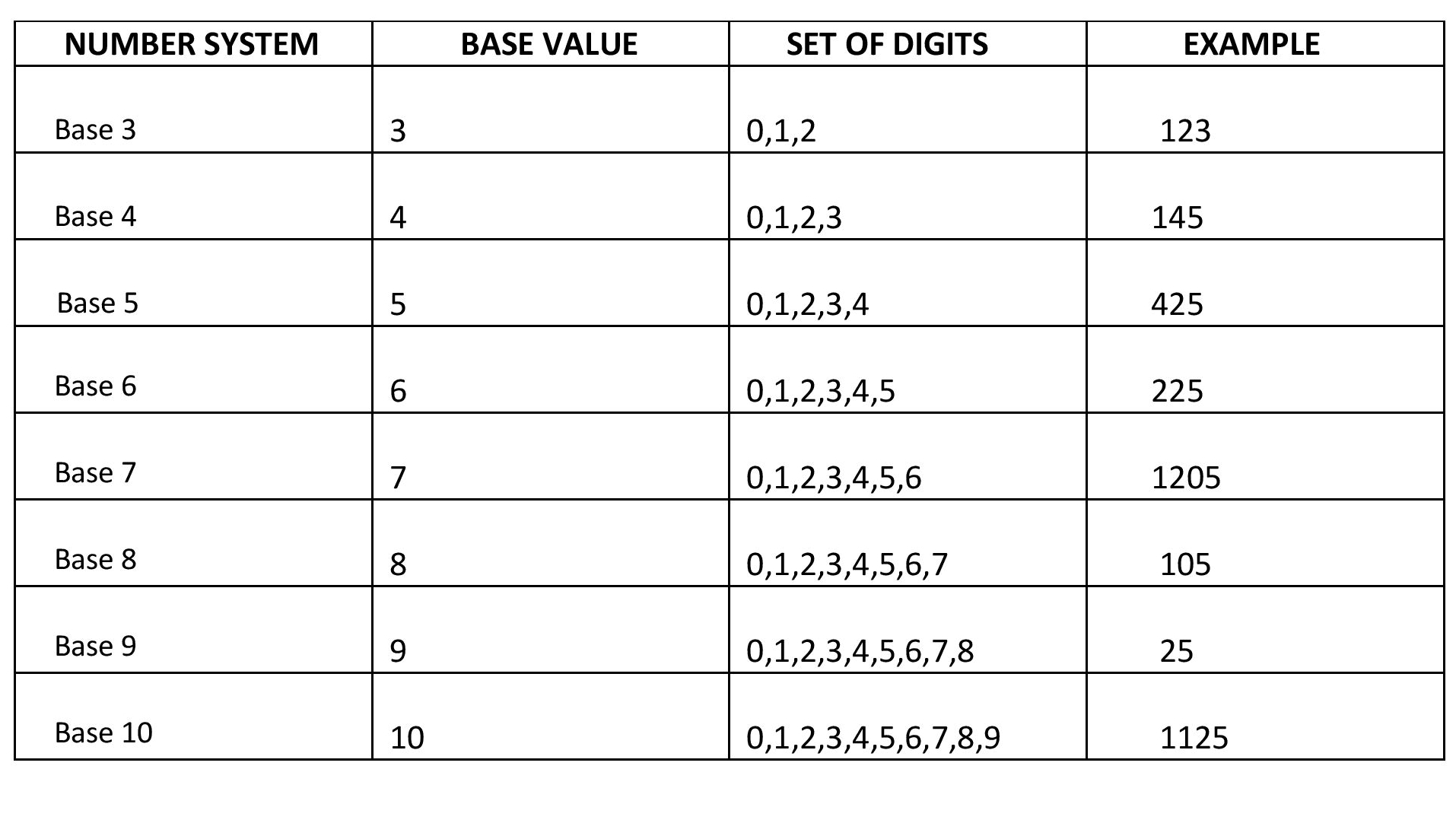
The numbers are represented as a base of something.In general we can say that base n.

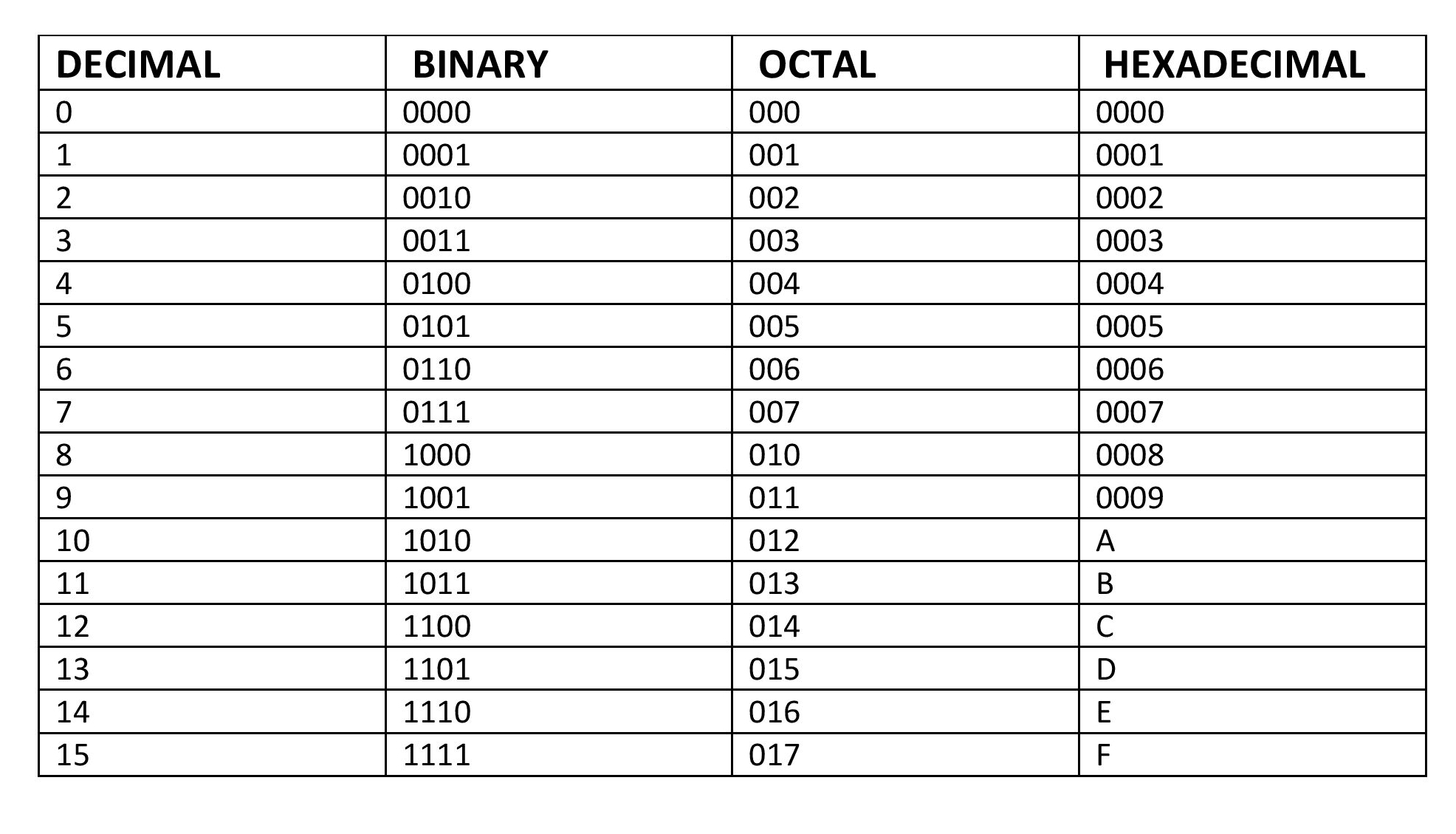
The same number in decimal,binary,octal and hexadecimal is shown below

Decimal Numbers

These are base 10 in number system.
The digits in decimal number system are 0,1,2,3,4,5,6,7,8,9.
Every digit position has a weight which is a power of 10.

As we go from right to left the significance of the position increases by 16 times, so the numeric value of a decimal number is determined by multiplying each digit of the number by the value of the position in which the digit appears and then adding the products.

Example:

The number 365 can be represented in decimal system as

3x10^2+6x10^1+5x10^0=300+60+5=365

Hexadecimal Numbers

These are base 16 in number system.
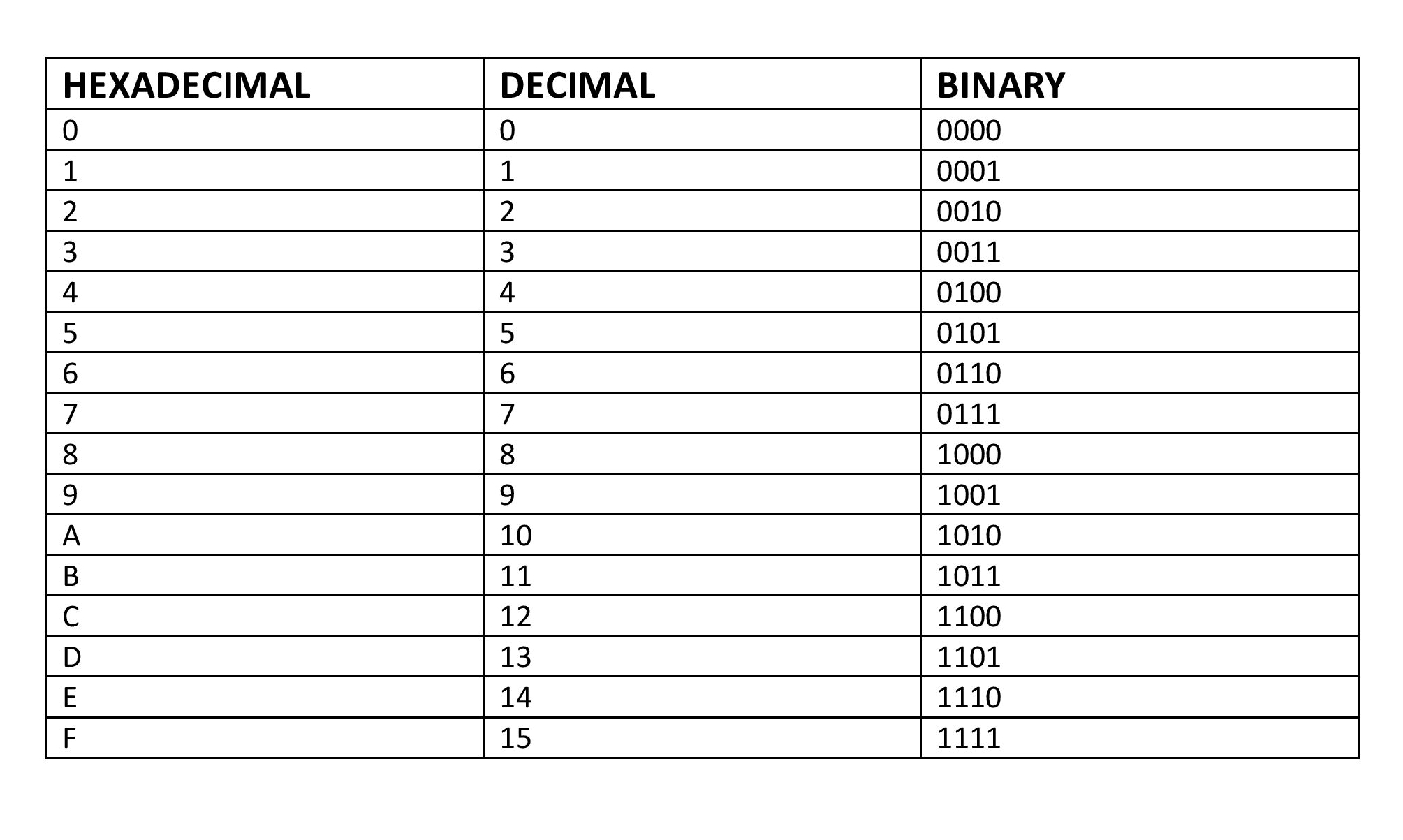
The digits in decimal number system are 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.

The A in Hexadecimal representation is equivalent to 10 in Decimal Number System.
The B in Hexadecimal representation is equivalent to 11 in Decimal Number System.
The C in Hexadecimal representation is equivalent to 12 in Decimal Number System.
The D in Hexadecimal representation is equivalent to 13 in Decimal Number System.
The E in Hexadecimal representation is equivalent to 14 in Decimal Number System.
The F in Hexadecimal representation is equivalent to 15 in Decimal Number System.

Every digit position has a weight which is a power of 16.

As we go from right to left the significance of the position increases by 16 times, so numeric value of a Hexadecimal number is determined by multiplying each digit of the number by the value of the position in which the digit appears and then adding the products.As we go from right to left the significance of the position increases by 16 times, so numeric value of a Hexadecimal number is determined by multiplying each digit of the number by the value of the position in which the digit appears and then adding the products.

Example:

The number 365 can be represented in Hexadecimal system as

3x16^2+6x16^1+5x16^0

Algorithm for Conversion of Decimal to Hexadecimal

1.Divide the decimal number by 16. Treat the division as an integer division.
2.Write down the Quotient.
3.Write down the remainder (in hexadecimal).
4.Repeat step 1,2 and 3 until Quotient is 0.
5.The hex value is the digit sequence of the remainders from the last to first.

Program Implementation

Code In C

#include <stdio.h>
 
int main()
{
    long decnum, quo, rem;
    int i, j = 0;
    char hexnum[100];
 
    printf("Enter decimal number: ");
    scanf("%ld", &decnum);
 
    quo = decnum;
 
    while (quo != 0)
    {
        rem = quo % 16;
        if (rem < 10)
            hexnum[j++] = 48 + rem;
        else
            hexnum[j++] = 55 + rem;
        quo = quo / 16;
    }
 
    
    for (i = j; i >= 0; i--)
            printf("%c", hexnum[i]);
    return 0;
}

Input

Enter decimal number: 9999

Output

270F

...Program finished with exit code 0
Press ENTER to exit console.

Example with Detailed Explanation.

We are recording the results obtained in a table of 2 columns - QUOTIENT and REMAINDER

QUOTIENT	REMAINDER
-	-
-	-
-	-

NOTE:The value in REMAINDER column is in hexadecimal.So if 10,11,12,13,14 or 15 comes write A,B,C,D,E,F respectively to the column.

Convert the DECIMAL number 456 to HEXADECIMAL.

Steps:

Divide the decimal number by 16. Treat the division as an integer division.

456/16

The Quotient is 28 and is written to the Quotient Column

The Remainder is 8 .The Hexadecimal Equivalent of 8 i.e, 8 is written to the column Remainder.

QUOTIENT	REMAINDER
28	8
-	-
-	-

Now divide the Quotient with 16 .

28/16

The Quotient is 1 and is written to the Quotient Column

The Remainder is 12 .The Hexadecimal Equivalent of 12 i.e, C is written to the column Remainder.

QUOTIENT	REMAINDER
28	8
1	C
-	-

Now divide the Quotient with 16 .

1/16

The Quotient is 0 and is written to the Quotient Column

The Remainder is 1 .The Hexadecimal Equivalent of 1 i.e, 1 is written to the column Remainder.

QUOTIENT	REMAINDER
28	8
1	C
0	1

As the quotient has become Zero we will stop here and will examine the Remainder column of the table obtained

QUOTIENT	REMAINDER
28	8
1	C
0	1

We will write digit sequence of the remainders from the last to first.This is our required Hexadecimal value.

Therefore the hexadecimal equivalent of 456 is 1C8.

Example With the table Illustration

Convert the Decimal number 1695 to Hexadecimal.

Initially

QUOTIENT	REMAINDER
-	-
-	-
-	-

1695/16

QUOTIENT is 105
REMAINDER is 15 whose hexadecimal equivalent is F.

QUOTIENT	REMAINDER
105	F
-	-
-	-

105/16

QUOTIENT	REMAINDER
105	F
6	9
-	-

6/16

QUOTIENT	REMAINDER
105	F
6	9
0	6

Therefore the hexadecimal equivalent of 1695 is 69F.

Examples to Workout.

1. Convert 2789 to Hexadecimal

QUOTIENT	REMAINDER
174	5
10	E
0	A

Therefore the hexadecimal equivalent of 2789 is AE5.

2. Convert 689 to Hexadecimal

QUOTIENT	REMAINDER
43	1
2	B
0	2

Therefore the hexadecimal equivalent of 689 is 2B1.

3. Convert 999 to Hexadecimal

QUOTIENT	REMAINDER
62	7
3	E
0	3

Therefore the hexadecimal equivalent of 999 is 3E7.

4. Convert 55932 to Hexadecimal

QUOTIENT	REMAINDER
3495	C
218	7
13	A
0	D

Therefore the hexadecimal equivalent of 55932 is DA7C.

5. Convert 345 to Hexadecimal

QUOTIENT	REMAINDER
21	9
1	5
0	1

Therefore the hexadecimal equivalent of 345 is 159.

Game Time

1 -D
2 -J
3 -B
4 -O
5 -G
6 -O
7 -O

Given above are the Alphabets Equivalent to numbers

Convert 21601 to hexadecimal.
Find the Alphabets corresponding to the result obtained and concatenate them.

Convert 627 to hexadecimal.
Find the Alphabets corresponding to the result obtained and concatenate them.

Now write the first word obtained put a space and write the second word.
That's my message to you!!

Yay, thus we have reached the end of this article at OpenGenus. We have learned how to convert decimal to hexadecimal and played a game to reinforce the idea!!