Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored several Data Structures that are used in Spreadsheet / Excel Sheet. These involve ideas like Sparse Matrix, AVL Tree and much more.
Table of contents:
- Introduction to Spreadsheet / Problem Statement
- simple bruteforce way
- a lazy way
- sparse matrix
- openoffice's implementation
- using AVL Tree
Pre-requisites:
Introduction to Spreadsheet / Problem Statement
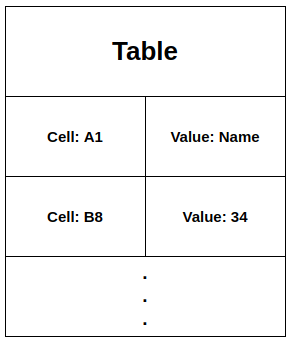
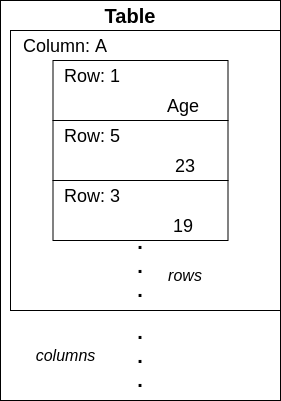
If you have used Excel Sheet from Microsoft or Calc from OpenOffice then you must have seen that the whole Spreadsheet looks like a table,
Where it has columns as A, B, C, ... and row as 1, 2, 3, ...
Let's say you want to make your Spreadsheet Application and you simply took the whole table as a
2D Array!!.
The problem with this is that you would be occupying lots of memory that you don't even require because lots of your cells are just empty.
That's why you could use many other ways to store your cells and data without occupying lots of unnecessary memories. And we will be seeing one of those ways in this article, going to go through how to implement it, especially one method that is known to be used by Excel Sheet is using Binary Tree.
Notes:
Accessword refers to accessing a cell in the spreadsheet using its row and column.
Index
The Bruteforce Way
Using directly 2D Matrix would be simple and straightforward to store the whole Spreadsheet because you don't have to every time create or delete a piece of memory.
But this will be a really bruteforced method to store the values since, normally no one will be using that whole reserved memory.
You might have another reason to not use this is that you will be defining a static 2D array.
But let's say you're using the whole space, and you're not deleting or inserting any new values at random positions, then this would be a great choice ( simple and fast, but for only this case).
Inserting
Since, we're defining a static 2D Array here, therefore, you cannot extend it, but let's say you did define a dynamic array then, you may perform two kinds of insertion, i.e.
1. Inserting a column
Doing this will require you to first decide at what place you want to insert a new column(by index), and then you need to shift the whole array of a column into a new array while creating a new empty row of the same size as the other rows.
Complexity: O(N)
2. Inserting a row
Now this could be done in two ways,
- insert one row in one column, hence, losing the rule of the same size of the column and same size of the row.
- insert one row in every column, hence, replacing every column array with a bigger one, So, it could fit a whole new row, while maintaining the Square Matrix.
Complexity: O(N2)
Inserting a cell would shift all other values which will deform the integrity of your data, therefore, inserting a cell in this data structure is not possible.
Deleting
Actually while deleting a cell in this Matrix will shift the other values unlike the other data structure we're going to see afterward, therefore a cell isn't possible.
But if you need you can delete a column or a row.
1. Deleting a column
When we delete a whole column ( so, deleting one array of rows ), we will require to shift the whole columns after that to fill the place.
Complexity: O(N)
2. Deleting a row
The whole sequence of a row is separated throughout the columns, therefore we would have to delete a row and shift the whole other rows to fill the space for every column.
Complexity: O(N2)
Searching
When searching a value in this data structure we would require to look at every (both empty and non-empty) cell.
Therefore, the cells we need to check will be row * col.
i.e. Searching Complexity will be: O(N2)
Complexities
- Space :
O(N2)- Insert :
Cannot be done.- Delete :
Cannot be done.- Search :
O(N2)- Access :
O(1)
Nis the number of rows/columns considering that the row and column have the same length and form Square Matrix.
The Lazy Way
Will discuss this one first because it's simple and easy, and it provides an idea to make it easy to continue to a sparse matrix.
But I'm not sure if it should be used anywhere.
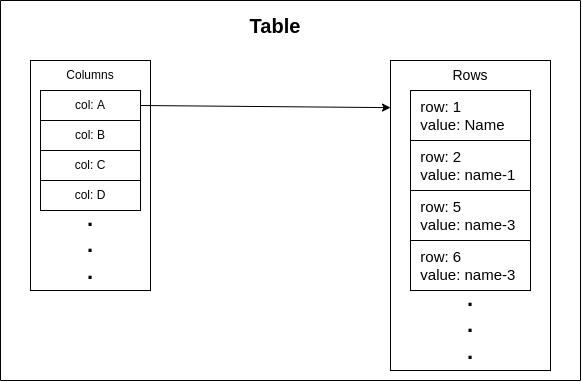
In this approach, whenever their is value available for a cell then we store both the value and the position of the cell together, this could be done using JSON as mentioned in above link. Or you could try some of your other ways such as HashMap also known as Dictionary.
Few examples:
1. In JSON with Cell and Value.
2. A little variation
Here, we're using HashMap as above, except instead of storing it by Cell (position value), first, we have HashMap for columns, and then each column has another HashMap for a cell.
This solution is more like a variant ofSparse Matrixthat we will see next.
Inserting
If you have used HashMap before then you may know that you require a value for your position/index ( to generate a hash value ) and then a value that you want to store at that index.
So, if we're using the above method of nested column and row, then,
Steps to insert a value will be:
- Check if the column you need exists or not, if it doesn't then make an entry for the column with the position values such as
A, B, C, ...or you can also use1, 2, 3, ..., and create aHashMapto store rows.- Then Check for the row position value and make Entry if not available.
Complexity: O(1)
Deleting
Check like for the Entry as above we did while inserting the value and delete the entry for the row and if there aren't any available rows in that column then also delete the entry for the column.
Complexity: O(1)
Searching
Searching will require us to look through all the entries, So:
- we would have to go through every Entry for rows and check if the value is the one we're searching for
- and step one would have to be performed on every column.
Complexity: O(N)
Complexities
- Space :
O(N)- Insert :
O(1)- Delete :
O(1)- Search :
O(N)- Access :
O(1)
Nis the number of entries made.
Sparse Matrix
The concept of Sparse Matrix is used when most of the element available in a matrix is zero, And when we're dealing with a Spreadsheet then this is the case for most of the time.
In Sparse Matrix instead of storing the values in 2D Array, we take three different arrays to store the values of the column, row, and the values that reside there.
Three Arrays:
- Values => Stores the user given values that you see in cells.
- Row => Stores the row value of the cell.
- Column => Here every index represents the column, and this array stores the index value at which the rows start, in the Row array.
Something like:
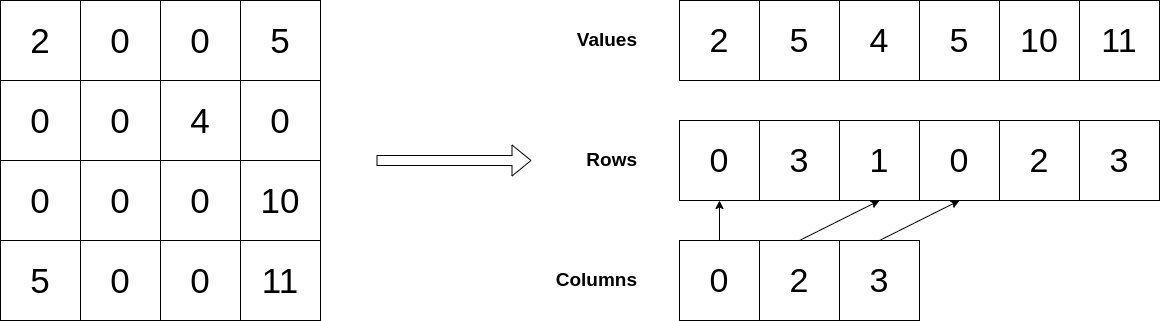
Before we proceed, let's assume you have
colandrowas your position forColumnandRowrespectively andvaluethat you need to add on theValuearray.
Inserting
To insert a value in Sparse Matrix we will need to alter all three arrays in one order,
- Column
- First we will check if is there any value available at
Column[col]that is notnullor any value that you decided to use to show that "this Column has no value",- If
Column[col]is empty then find the next column that is available take its value, let's call itrow_iand setColumn[col] = row_i(skip 5th step).- And
Column[col]have any value then increment values of theColumn[col]and for every values after that.
- Row
- Now, if you found not NULL value at
Column[col], then go toRow[Column[col]]( let's takeRow[Column[col]]asrow_i).- Now, increment
row_iand find the value which is greater than yourrowor else yourrow_ibecomes greater thanColumn[next_column].- Shift the whole values starting from
row_ito make a space inRowarray and then doRow[row_i] = row.
- Values
- Now only insertion is remaining, take
row_ifrom there shift every value towards the end of the array by 1, and now put thevalueatValue[row_i].
Pseudocode
def next_column(pre):
next_col = 0
for i in range(pre, len(Column)):
if Column[i] is not Null:
next_col = Column[i]
break;
return next_col
get col, row, value;
row_i = 0
if Column[col] is Null:
row_i = next_column(col)
Column[col] = row_i
else:
row_i = Column[col]
next_col = next_column(row_i)
for i in range(row_i, Column[next_col] + 1):
if Row[i] > row:
row_i = i
break;
elif i == Column[next_col]:
row_i = Column[next_col] + 1
for i in range(col, len(Column)):
Column[i] += 1 if Column[i] is not Null
Row.insert(row_i, row)
Value.insert(row_i, value)
Deleting
Let's look at steps for deleting a value from the Matrix here again we would be using the row and col
- Column
- Get the
row_ifromColumn[col].- Now, decrement the values in the
Columnarray starting fromcolto the end ofColumn.
- Row
- Find the row by incrementing
row_iand checking the value in the Row array until you reachColumn[next_column].- Now shift all
rowstarting from therow_ito the end of theRowarray, towards left by 1.
- Value
- And then shift all the
valuein the Value array towards the left by 1, fromrow_ito the end of theValuearray.
Pseudocode
get row, col;
row_i = 0
if Column[col] is not Null:
# step 1
row_i = Column[col]
# step 2
for i in range(col, len(Column)):
Column[col] -= 1 if Column[col] is not Null
# step 3
next_col = Column[next_column(col)]
for i in range(row_i, next_col + 1):
if Row[i] == row:
row_i = i
elif i == next_col:
return;
Row.delete(row_i)
Value.delete(row_i)
Searching
Searching in Sparse Matrix should be possible through the Linear Search.
This time we will be going from the array Value and then to the Row and then Column.
- Value
Here you can perform a Linear Search to find the index at which our
valueresides. - Row
Now, after we know index for value, we know index for the row as well, therefore,
row = Row[index]. - Column
Also, here do Linear Search and find a value that is equal to
indexand return that as acol, and if you find a value that is greater thanindexthen return the previousindexwhich was notNull.
Pseudocode
get value;
index = 0
row = 0
col = 0
# searching the value
for i in range(len(Value)):
if value == Value[i]:
index = i
# got the row
row = Row[i]
break;
# searching for the col
pre_i = 0
for i in range(len(Column)):
if Column[i] is not Null:
if Column[i] > index:
col = pre_i
break;
elif Column[i] == index:
col = i
break;
pre_i = i
return (col, row)
Complexities
- Space :
O(N)- Insert :
O(N)- Delete :
O(N)- Search :
O(N)- Access :
O(1)
OpenOffice's Implementation
Mentioning this here only as an example to the Sparse Matrix.
We're not going to go through the whole thing but only the idea that they have used here to store the cells because a lot of things happen in a Spreadsheet than just storing the values like, you have to provide support for multiple kinds of data types and also a possibility to perform the operations regarding them.
If we look at the OpenOffice doc for data model of cell and sheet, we notice that they use 1024 columns and that's the max value for a column, and after this, the column stores only values for non-empty rows.
To imagine all this.
You can notice that the column is going in one order, but that is not compulsory with the rows.
AVL Tree
AVL Tree is a Binary Search Tree with some extra steps, which allows it to balance itself.
I recommend you to read about AVL and BST before you proceed on this topic of using AVL as a data structure for a Spreadsheet.
In this approach we will use Nodes of the AVL Tree store three values in tree row, column and value, and in that we will use the values of row and col to make comparisons in the AVL Tree.
We can have two variants regarding this:
1. One-Tree
One Tree is not an official name or anything, but just a name popped up in my head while organizing this article.
In this variant, we will store all three col, row and value, in one Node and only one AVL Tree will be created ( therefore, every value will be stored by one AVL Tree).
The comparison between Nodes can be done using both col and row values while giving more priority to one than the other,
Giving more priority to:
- col
If we look at some values while giving priority to
colfor comparisons, then it looks something like,
A1 < A2 < A3 ... < B1 ... < C1 ...
So, you see no matter whatrowyou select inAit will always be less than theBn.
- row
Like
col, if we give priority torowthen allA1,B1,C1, ... will be less than theA2,B2,C2,...
And if said in short anyx1will be less than anyx2and so on.
Well, here I'm not sure what kind of difference there will be in performance, but we're going to choose to give more priority to the column because it would separate every row into different Sub-Tree of a column.
2. Nested-Tree
Another way to do this is to have a different AVL Tree for column and row. Every Node in AVL Tree for column need to contain a pointer to the AVL Tree of rows and this Tree for row contains Cells of the Spreadsheet.
You might notice that structure of this is not different than the above One Tree while we're giving priority to the col.
Operations
Now let's discuss how to implement this thing, well, we're going to look at the Nested-Tree, because if you want to implement the One-Tree method then we would need to implement the whole AVL Tree instead of using an already built one or maybe you could try features like such as operator overloading or any feature that a programming language might provide.
Therefore, for now, let's just only focus on Nested one.
Inserting a value
For this, we would need row, col, and value
the first step would be, to see if col is available or not,
- if it is available then, use the pointer to the Tree of row and insert the Node for the
rowwith thevalue - And if it's not available then, create an AVL Tree with root Node of
rowwhich containsvalueand then insert the Tree pointer in theTree of column.
pseudocode
get row col value
if Columns.has(col):
Rows = Columns.get(col)
Rows.insert(Node(row, Cell(value)))
else:
Rows = Tree()
Rows.insert(Node(row, Cell(value))
Columns.insert(Node(col, Row))
Deleting a value
Deleting a value in this is simpler than Inserting a value,
We will only need row and col of the Cell we need to delete.
First, we need to search the Node for col in Columns's Tree and then check if the Rows Tree have only one row that we need to delete then, delete the Node for col in Columns Tree directly or else only delete the Node Rows's Tree.
Pseudocode
get row col
global Columns
if Columns.has(col):
Rows = Columns.get(col)
if Rows.len() == 1:
Columns.delete(col)
else:
Rows.delete(row)
Searching a value
Since we're finding a value, therefore, we need the value for this operation.
After we have value we need to look at every Node in every Rows Tree and check if the Node has the value we need.
This operation would be easier to do, if your AVL Tree is made up of an array since, you have to only iterate through it, else if it's made up of Nodes pointing to their children then you will require more codes to do this.
We will look at both of these.
- If Tree is Array
Pseudocode
get value
global Columns
for col in range(len(Columns)):
for row in range(len(Columns[col].rows)):
if Columns[col].rows[row].value == value:
return(col, row)
- If Tree is Nodes
Pseudocode
get value
global Columns
class Tree:
# This is generator which will run recursively
# provides the next node everytime it's called.
def next(self):
if self.left is not Null:
yield self.left
self.left.next()
if self.right is not Null:
yield self.right
self.right.next()
for _ in range(Columns.len()):
node = Columns.next()
(col, Rows) = node.col, node.rows
for _ in range(Rows.len()):
node = Rows.next()
if value == node.value:
return (col, node.row)
Complexities
- Space :
O(N)- Insert :
O(logN))- Delete :
O(logN)- Search :
O(N)- Access :
O(logN)
Extras
Well, we're done here, but I will consider the above concepts are hard to understand, and for that, I have written examples in python for all the concepts mentioned above in this repo.