Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Problem Description: Given a Linked list, find out whether it contains a loop or not. If it does, then remove the loop and make the last node point to NULL.
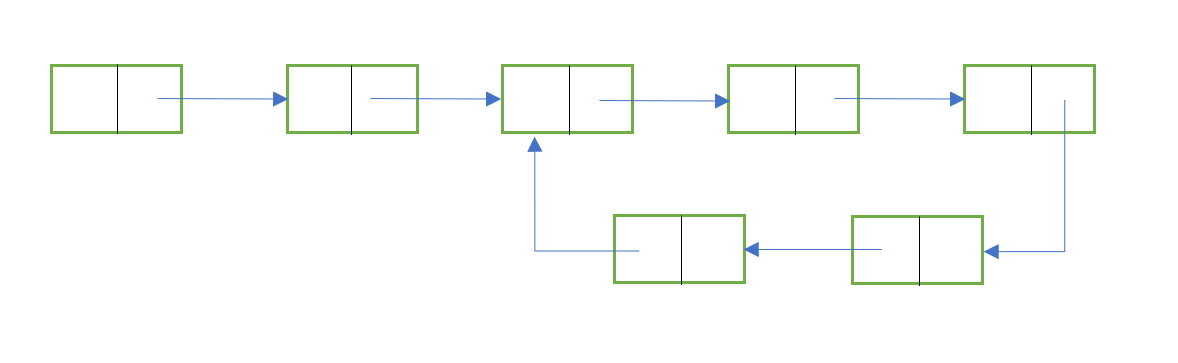
In a linked list, a loop is encountered when the last node points to any node in the linked list instead of pointing to NULL.
For eg:
To solve this problem, we need to follow these 2 steps:
- Detecting whether a loop is present or not.
- Removing the loop.
Detecting a loop in Linked List :
The fastest method to detect a loop in a linked list is the Floyd's Cycle-Finding Algorithm.
This method uses 2 pointers, one moving faster than the other while traversing.
It works as follows:
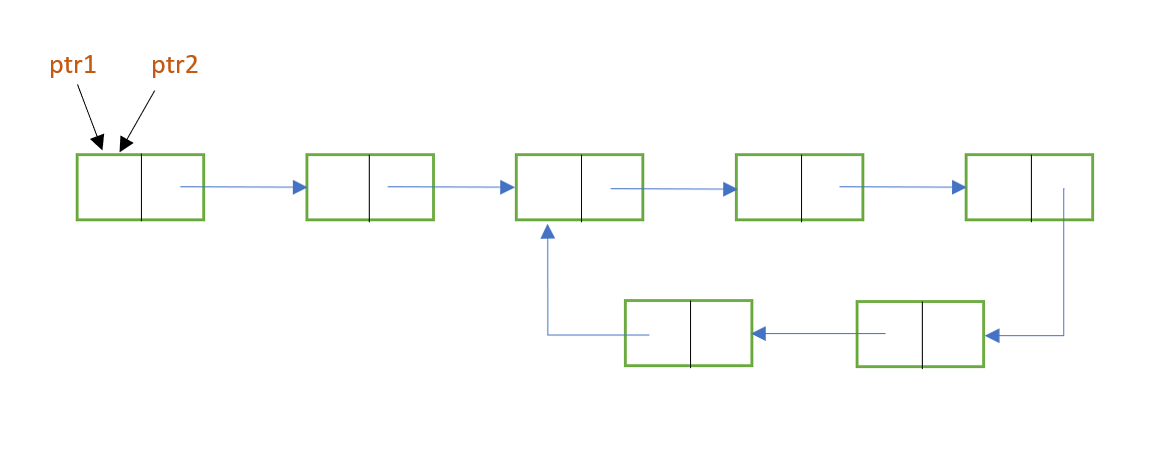
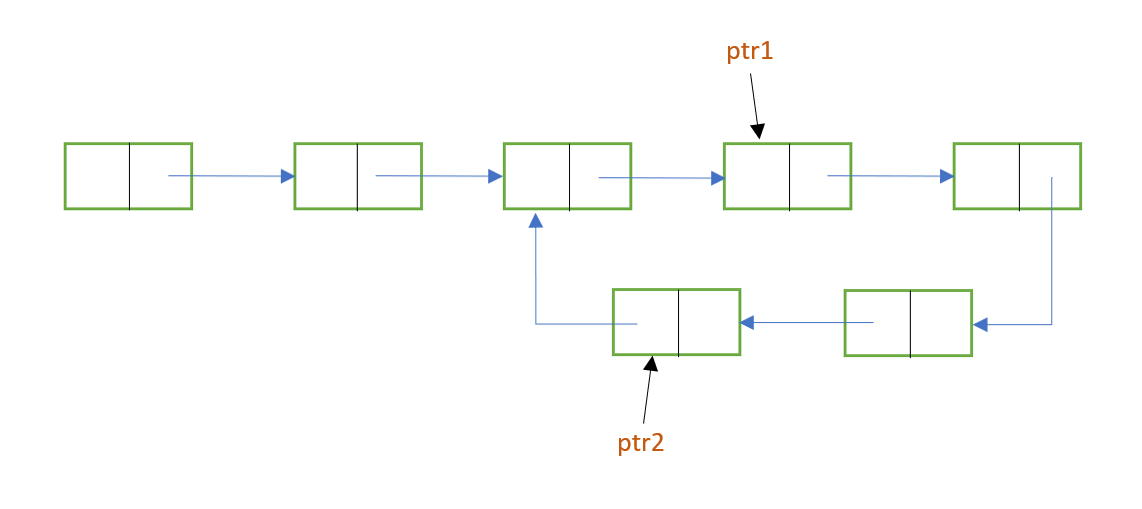
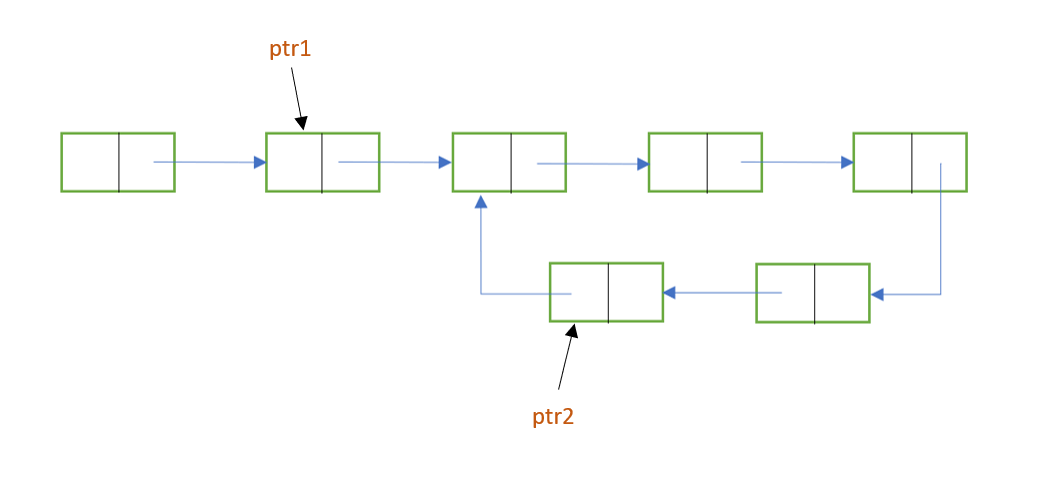
- Two pointers, let's say ptr1 and ptr2, are initialised with the head node.
- While traversing the list with these pointers, move ptr1 one node at a time, whereas move ptr2 two nodes at a time.
- As ptr2 moves faster than ptr1, it will reach the end of the list first. Now, there are 2 possible cases:
a) There will be no loop in the linked list. If this is the case, ptr2 or ptr2->next will be NULL. This is because ptr2 moves 2 nodes at a time. So, if there are even no. of nodes in the list, ptr2 will eventually become null. And if there are odd no. of nodes, then ptr2->next will become null. When null value is encountered, we can stop the execution and display the output as "no loop".
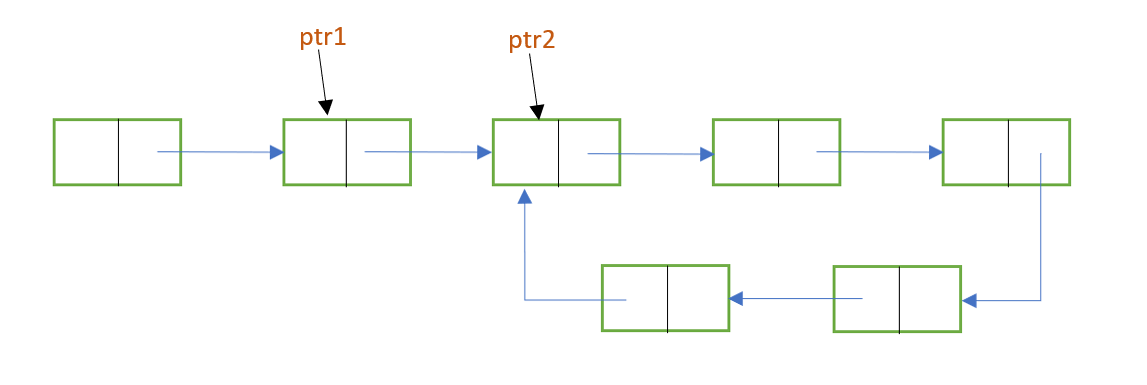
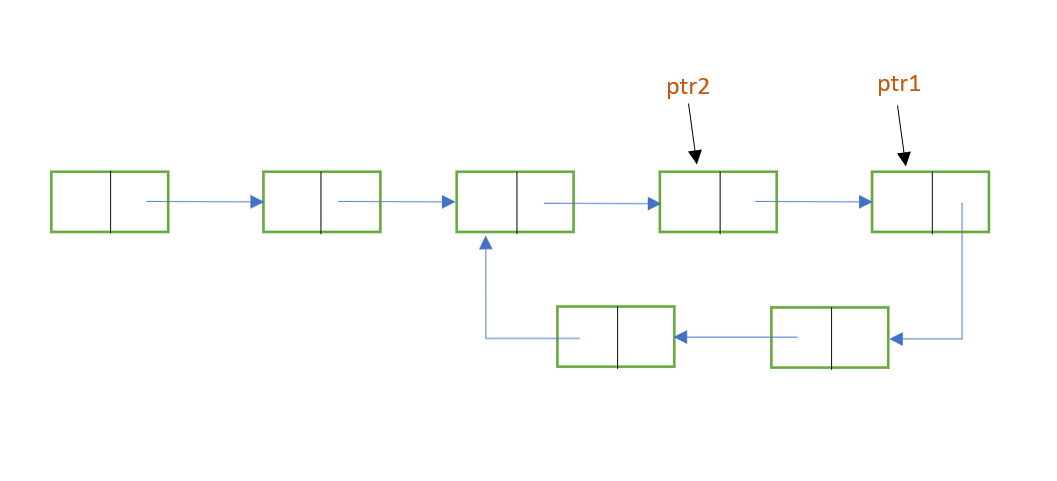
b) There is a loop in the linked list. When this is the case, the pointers won't reach a null value. Instead, they'll enter the loop and traverse there. Further, at some point, both the pointers will meet at the same node. This is because both the pointers start traversing in a loop with different speeds. Hence, they are bound to meet eventually. When this happens, ptr1 = ptr2 , and we can stop the execution with the output "loop is present".
The following images show the implementation of Floyd's Cycle-Finding ALgorithm:
Hence, the 2 pointers will eventually meet at some node in the cycle.
So let's move on to the next part of this problem!
Removing the loop in a linked list
Now that we have detected a loop in the list, it's time to remove that loop by pointing the last element to NULL.
The following steps depict the procedure:
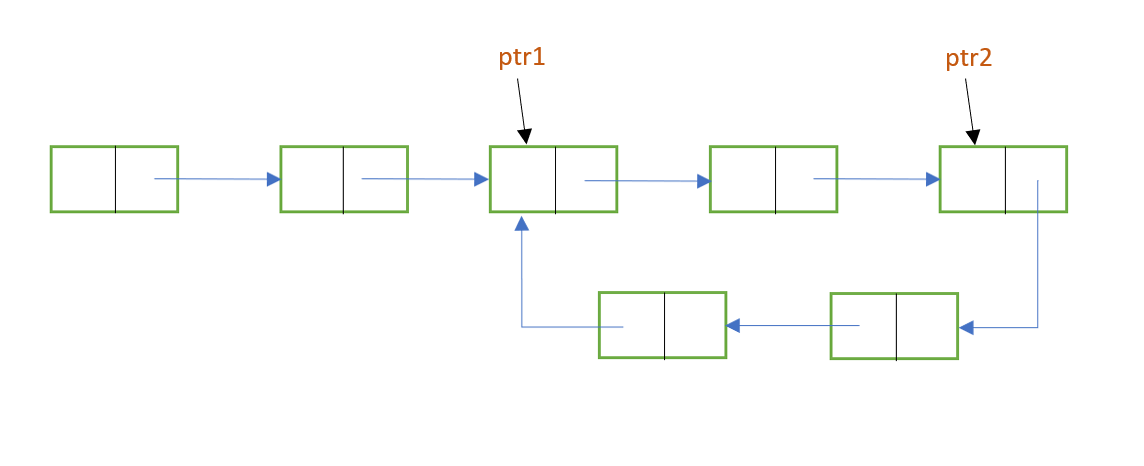
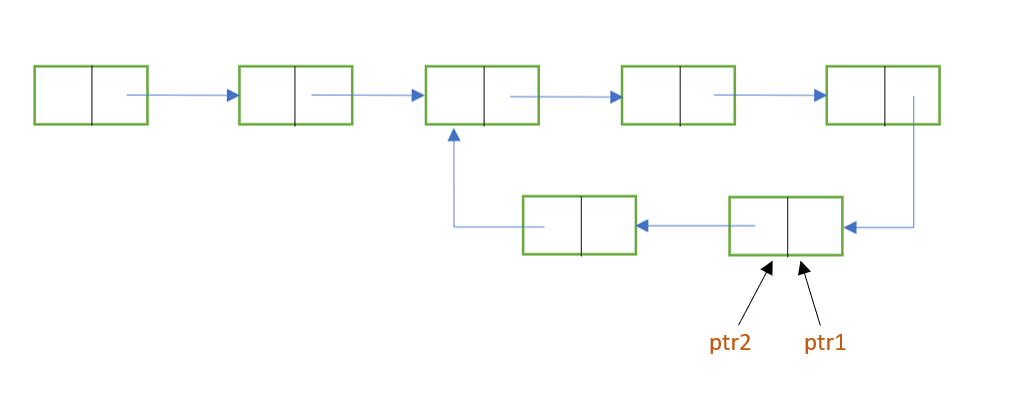
- As we know, if a loop is found, then ptr1 and ptr2 will point to the same node inside the loop. We need to find the last element of the loop and make it point to null.
- For that, make ptr1 point to head and leave ptr2 where it is.
- Now traverse these pointers through the list. This time, both ptr1 and ptr2 will move at the same speed i.e one node at a time. Do this until the next pf ptr1 and next of ptr2 will meet. The node where they will meet will be the node where the loop starts.
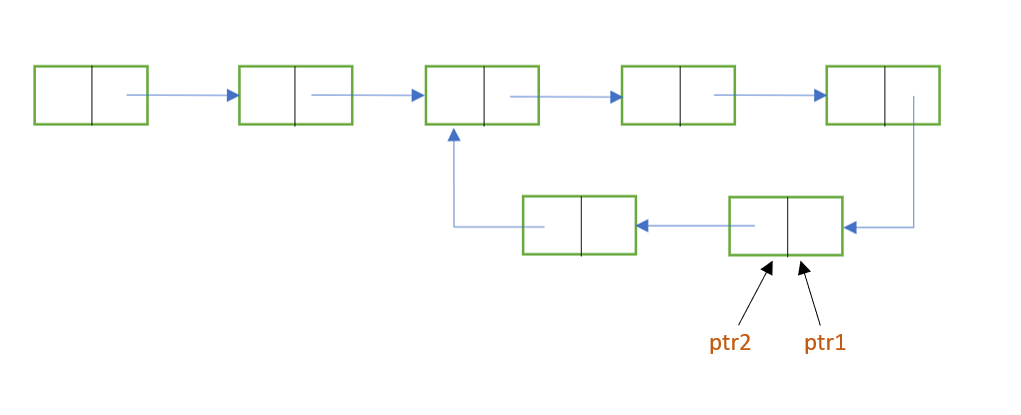
- To remove the loop, make the next of ptr2 point to NULL.
Here, we need to keep in mind that the next of both ptr1 and ptr2 will always meet at the node where the loop starts. You may wonder why this is the case.
How is it that the next of both pointers will meet at the starting node of the loop?
Let's understand this with a general example.
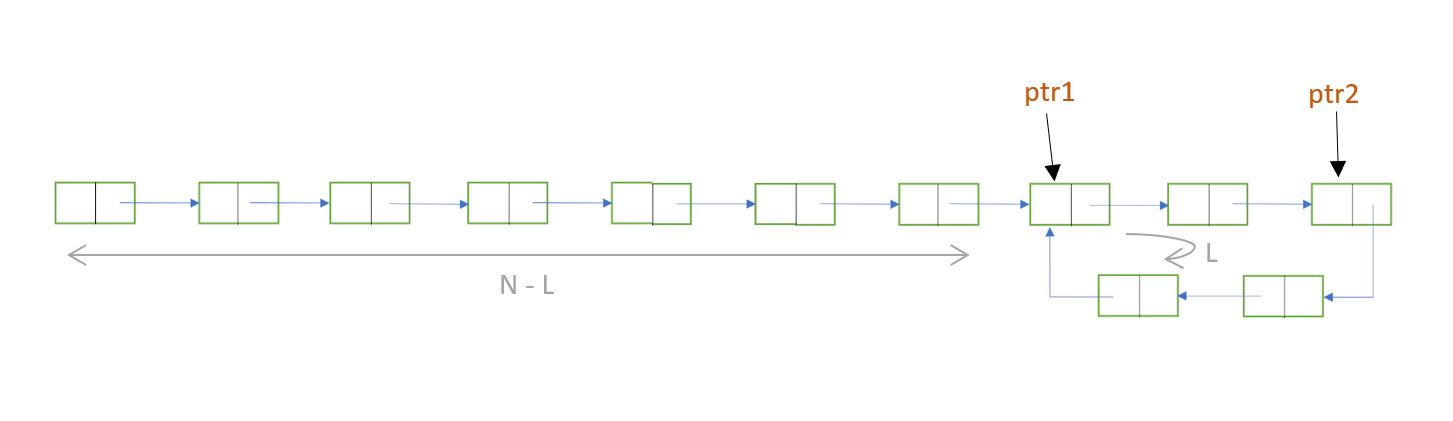
N = no. of nodes in the list.
L = no. of nodes in the loop.
In our example, N = 12 and L = 5
We start with ptr1 and ptr2 both being at the head node.
To reach at the starting node of the loop, ptr1 needs to move N-L steps i.e 7 steps in our case.And, as ptr2 moves twice as fast as ptr1 , ptr2 needs to move 2*(N-L) steps i.e. ptr2 will move (N-L) extra steps than ptr1.
Hence, the distance between ptr1 and ptr2 will be (N-L)%L i.e (12-5)%5 = 2 nodes.
This is because ptr2 moves through the whole loop to cover (N-L) nodes.
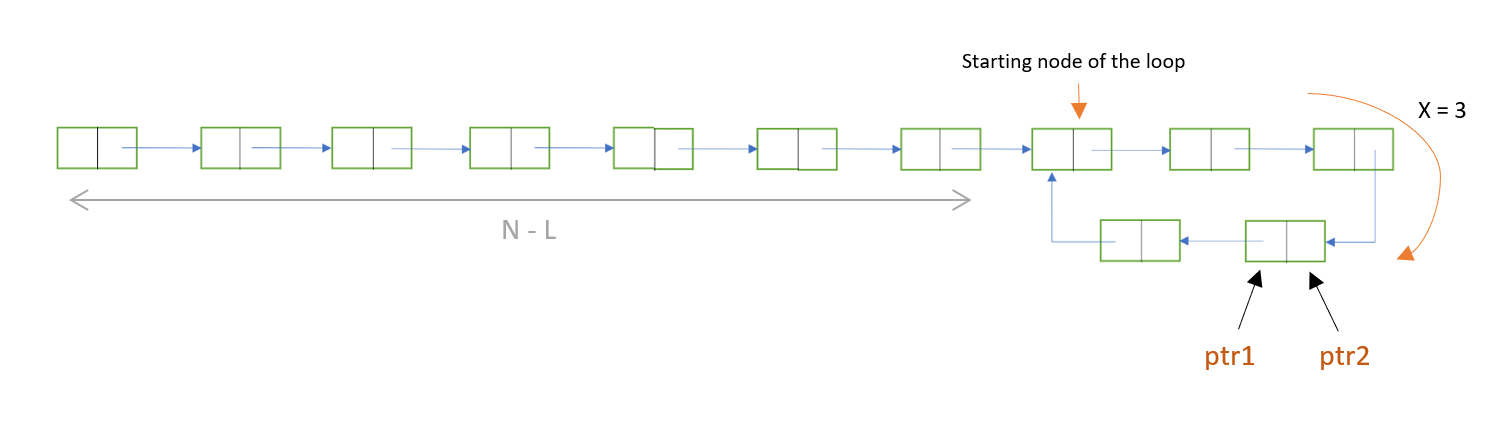
In the next step, the distance between ptr1 and ptr2 will be (N-L)%L + 1 .In the step after that, it will be (N-L)%L + 2 and so on...
Hence, the distance between ptr1 and ptr2 will be (N-L)%L + x , where ptr1 will travel 'x' nodes from the starting point of the loop.
However, we need to stop the execution when ptr1 and ptr2 will meet. They will meet when the distance between them will be L, as ptr2 will move through the loop once and then meet with ptr1.
The distance between the pointers will be L, when
x = L - ( (N-L)%L )
In our example, x is 3.
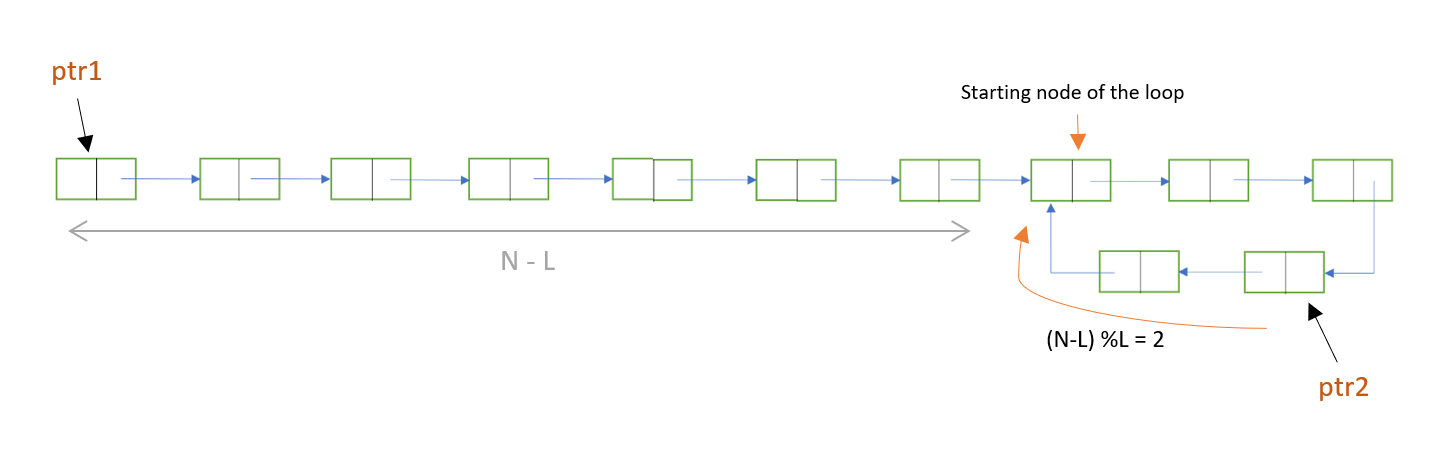
Now, we leave ptr2 where it is and bring back ptr1 to the head node. This time, ptr1 and ptr2 move at the same speed. ptr1 moves N-L nodes to reach to the starting node of the loop. Similarly, when ptr2 will move N-L nodes, it will also again reach the starting node of the loop, because ptr2 was (N-L)%L i.e. 2 nodes away from the starting point.
Hence, ptr1 and ptr2 will always meet together at the starting point of the loop.
So, to remove the loop, we can go one one step backwards, when ptr2->next will be the starting point, and then here, make ptr2 point to NULL.
Given below is the code in C language for the problem:
#include<stdio.h>
#include<stdlib.h>
//Definition of singly Linked List
struct node{
int data;
struct node *next;
};
void removeLoop(struct node* head){
int flag =0;
//Initialise ptr1 and ptr2 to head
struct node *ptr1 = head;
struct node *ptr2 = head;
//Detecting whether a loop is present or not
while(ptr2!=NULL && ptr2->next!=NULL){
ptr1 = ptr1->next;
ptr2 = ptr2->next->next;
if(ptr1==ptr2){
//When a loop is present
flag=1;
break;
}
}
//Removing the loop if it is present
if(flag == 1){
ptr1 = head;
//Traversing just before the starting node of loop
while(ptr1->next != ptr2->next){
ptr1 = ptr1->next;
ptr2 = ptr2->next;
}
//Make the last node point to NULL
ptr2->next = NULL;
}
}
int main(){
struct node *head = (struct node*)malloc(sizeof(struct node));
struct node *one = (struct node*)malloc(sizeof(struct node));
struct node *two = (struct node*)malloc(sizeof(struct node));
struct node *three = (struct node*)malloc(sizeof(struct node));
struct node *four = (struct node*)malloc(sizeof(struct node));
head-> data = 21;
head-> next = one;
one-> data = 45;
one-> next = two;
two-> data = 3;
two-> next = three;
three-> data = 78;
three-> next = four;
four-> data = 10;
four-> next = two;
//initiased the list with a loop
removeLoop(head);
//Printing the list
while(head!= NULL){
printf("%d -> ",head->data);
head = head->next;
}
printf("NULL");
return 0;
}
Output:
21 -> 45 -> 3 -> 78 -> 10 -> NULL
In the above code, we have initialised a list with a loop in it, and then we implemented Floyd's algorithm to remove that loop and successfully printed the list.