
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we will be discussing on how to find the level of each node in a graph, the algorithm that we will be using to find the level of each node is breadth first search so if you are not familiar with breadth first search , I would suggest you to first go through this article:
Read about Breadth First Search (BFS)then get back to this for better comprehension.
Level Of Each Node Using Breadth First Search
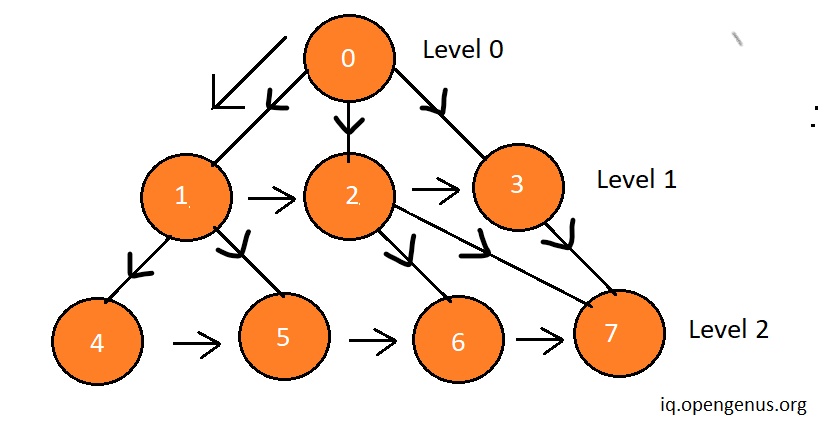
The above diagram summarises how breadth first search takes place in graph.
There are a few terminologies that you should know before going to the algorithm and code -
Root
The node from which we start our breadth first search traversal is called the root
or source node.
Level
The level of a node is defined by 1 + the number of connections between the node and the root.
Leaf Node
Any node whose left and right child are null is called the leaf node of the graph.
Algorithm
Step 1 : Set level of root node as 1.
Step 2 : Pop the first element in the queue and
enqueue all the nodes which are directly connected to the
popped element.
Step 3 : Set the level of all the element which are enqueued in the
previos Step to 1 more than element popped in the second step.
Step 4 : Repeat process 2 and 3 until the queue is empty.
Step 5 : Exit
Explanation
-
This algorithm follows breadth first search algorithm at it's core.
-
After the graph has been created we will set the level of the root node
in the level vector as 0 and then apply the breadth first search. -
In this algorithm we will pop the first element of the queue and set the
level of all of it's connected nodes as 1 more then the element popped from
the queue and simulatenouly push the connected nodes in the queue. -
We just keep repeating this process explained in until queue is empty.
-
At the end we will have level of all the nodes in the graph with respect to the root node.
Example
The graph shown below is a 3 level graph ( level 0 , 1 and 2 ) and we can find the level of each node in the graph using breadth first search .
First we will create the directed graph and the process of creation of graph is shown in the code section.
we will also create a level vector which stores the level of each node .
-
In the process , first we will set the level of node 0 ( root node ) as 0 and enqueue it in the queue.
-
Now , we will pop the first element of the queue ( which is 0 initially ) and push all the neigbouring nodes ( 2 and 3 ) in the queue and set level of all the neigbouring nodes 1 more then the node element we just popped from the queue.
-
Now we have node 1 , 2 and 3 in the queue , now we will repeat the same process explained in the above step , first we will deque the first element ( node 1 ) and set the level of neighbouring nodes( node 4 and 5 ) to more then the first node which we just dequeued.
-
We will repeat the same process with nodes 2 and 3.
-
At last we will have 4 , 5 , 6 and 7 nodes in the queue so will just pop each element because there are no neigbouring elements to these elements which are unvisited.
-
Now , we will just print the level vector which describes the level of each node.
Code
#include <iostream>
#include<vector>
#include<queue>
using namespace std;
void createEdge( int a , int b , vector<int> graph[] ){
// creating directed edge between nodes of the graph
graph[a].push_back(b) ;
}
vector<int> levelOrderTraversal( int root , vector<int> graph[] , int n ){
// creating a level vector for storing the data of level of each node
// compared to the root node
vector<int> level(n) ;
queue<int> q ;
// initially pushing the root in the queue and setting it's level as 0
q.push(root) ;
level[root] = 0 ;
// continuing this process uptill queue is empty
while( !q.empty() ){
int x = q.front() ;
q.pop() ;
// popping the first element and setting up the level of all the connected
// nodes to the current node
for( auto node : graph[x] ){
// setting up the level of node to 1 more then the current level
q.push(node) ;
level[node] = level[x] + 1 ;
}
}
return level ;
}
int main()
{
// first creating the graph
vector<int> graph[8] ;
for( int i = 0 ; i<8 ; i++ )
graph[i].clear() ;
// this is the same graph shown in the image at the beginning of the article
createEdge( 0 , 1 , graph ) ;
createEdge( 0 , 2 , graph ) ;
createEdge( 0 , 3 , graph ) ;
createEdge( 1 , 4 , graph ) ;
createEdge( 1 , 5 , graph ) ;
createEdge( 2 , 6 , graph ) ;
createEdge( 3 , 7 , graph ) ;
// applying the algorithm to find the level of all the nodes
vector<int> level = levelOrderTraversal( 0 , graph , 8 ) ;
// displaying each node and it's level in tabular format
cout<<"node "<<" level"<<endl;
cout<<"***************\n" ;
for( int i = 0 ; i<8 ; i++ ){
cout<<" "<<i<<"\t "<<level[i]<<endl;
}
return 0;
}
Output
node level
***************
0 0
1 1
2 1
3 1
4 2
5 2
6 2
7 2
Complexity Analysis
Time Complexity: O(n).
In BFS traversal every node is visited only once, so Time Complexity is O(n).
Space Complexity: O(n).
The space is required to store the nodes in a queue and also their level in the
vector.
Questions
To make sure that you understand the concepts answer these queshions:
