
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 11 minutes
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph
Dijkstra's algorithm is applicable for:
- Both directed and undirected graphs
- All edges must have nonnegative weights
- Graph must be connected
Dijkstra's algorithm was, originally, published by Edsger Wybe Dijkstra, winner of the 1972 A. M. Turing Award.

Explanation:
- Step 1: Set the distance to the source to 0 and the distance to the remaining vertices to infinity.
- Step 2: Set the current vertex to the source.
- Step 3: Flag the current vertex as visited.
- Step 4: For all vertices adjacent to the current vertex, set the distance from the source to the adjacent vertex equal to the minimum of its present distance and the sum of the weight of the edge from the current vertex to the adjacent vertex and the distance from the source to the current vertex.
- Step 5: From the set of unvisited vertices, arbitrarily set one as the new current vertex, provided that there exists an edge to it such that it is the minimum of all edges from a vertex in the set of visited vertices to a vertex in the set of unvisited vertices. To reiterate: The new current vertex must be unvisited and have a minimum weight edges from a visited vertex to it. This can be done trivially by looping through all visited vertices and all adjacent unvisited vertices to those visited vertices, keeping the vertex with the minimum weight edge connecting it.
- Step 6: Repeat steps 3-5 until all vertices are flagged as visited.
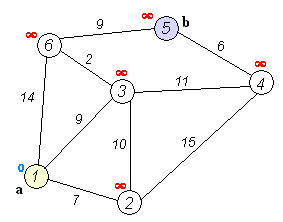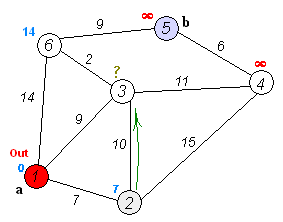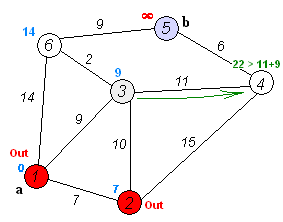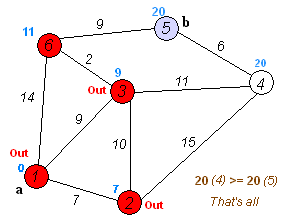
Visual: Finding shortest path from node (1) to all other nodes.
Pseudocode
dijkstra(v) :
d[i] = inf for each vertex i
d[v] = 0
s = new empty set
while s.size() < n
x = inf
u = -1
for each i in V-s //V is the set of vertices
if x >= d[i]
then x = d[i], u = i
insert u into s
// The process from now is called Relaxing
for each i in adj[u]
d[i] = min(d[i], d[u] + w(u,i))
Dijkstra's algorithm can be easily sped up using a priority queue, pushing in all unvisited vertices during step 4 and popping the top in step 5 to yield the new current vertex.
C++ code for Dijkstra's algorithm using priority queue: Time complexity O(E+V log V):
bool mark[MAXN];
void dijkstra(int v){
fill(d,d + n, inf);
fill(mark, mark + n, false);
d[v] = 0;
int u;
priority_queue,vector >, less > > pq;
pq.push({d[v], v});
while(!pq.empty()){
u = pq.top().second;
pq.pop();
if(mark[u])
continue;
mark[u] = true;
for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
if(d[p.first] > d[u] + p.second){
d[p.first] = d[u] + p.second;
pq.push({d[p.first], p.first});
}
}
}
Why it works?
-
Lemma 1: Optimal Substructure
The subpath of any shortest path is itself a shortest path. -
Lemma 2: Triangle inequality
If δ(u,v) is the shortest path length between u and v, δ(u,v) ≤ δ(u,x) + δ(x,v)
Complexity
- Worst case time complexity:
Θ(E+V log V) - Average case time complexity:
Θ(E+V log V) - Best case time complexity:
Θ(E+V log V) - Space complexity:
Θ(V)
Time complexity is Θ(E+V^2) if priority queue is not used.
Implementations
Implementation of Dijkstra's algorithm in 4 languages that includes C, C++, Java and Python.
- C
- C++
- Java
- Python
C
//for directed acyclig graphs!!
// Part of Cosmos by OpenGenus Foundation
#include<stdio.h>
#include<stdlib.h>
#define INF 999999
typedef struct node graph;
struct node{
int val;
graph *next;
int weight;
};
int src;
int wt_ans,val_ans;
int heap_count;
int flag[1000000];
struct node table[1000000];
struct node a[1000000];
void insert_vertex(int n){
int i;
for(i=1;i<=n;i++){
table[i].next=NULL;
table[i].weight=0;
}
}
void insert_edge(int x,int y,int w){
graph *one;
one=(graph*)malloc(sizeof(graph));
one->val=y;
one->weight=w;
one->next=NULL;
graph *tmp;
if(table[x].next==NULL){
table[x].next=one;
}
else{
tmp=table[x].next;
while(tmp->next!=NULL){
tmp=tmp->next;
}
tmp->next=one;
}
}
void insert_heap(int n){
int l,i;
for(i=1;i<=n;i++){
a[i].weight=INF;
a[i].val=i;
}
}
void update_heap(int x,int y){
graph tmp;
int l,k;
int i;
if(x==src && x!=1){
tmp=a[1];
a[1]=a[x];
a[x]=tmp;
a[1].weight=y;
}
else if(x!=src){
for(i=1;i<=heap_count;i++){
if(a[i].val==x){
k=i;
a[k].weight=y;
}
}
while((a[k/2].weight>a[k].weight)&&(k/2>=1)){
tmp=a[k/2];
a[k/2]=a[k];
a[k]=tmp;
k=k/2;
}
}
}
void extract_heap(int z){
graph tmp;
graph var;
tmp=a[1];
val_ans=tmp.val;
wt_ans=tmp.weight;
flag[a[1].val]=1;
a[1]=a[z];
heap_count--;
int k=1;
while((a[k].weight>a[2*k].weight || a[k].weight > a[2*k+1].weight) && (2*k<=z)){
if((a[k].weight>a[2*k].weight) && (a[k].weight <= a[2*k+1].weight)){
var=a[2*k];
a[2*k]=a[k];
a[k]=var;
k=2*k;
}
else{
var=a[2*k+1];
a[2*k+1]=a[k];
a[k]=var;
k=2*k+1;
}
}
}
int check_heap(int x){
int i,y;
for(i=1;i<=heap_count;i++){
if(a[i].val==x){
y=a[i].weight;
}
}
return y;
}
void print_table(int n){
graph *tmp,*var;
int i,j;
for(i=1;i<=n;i++){
printf("table[%d]",i);
tmp=table[i].next;
while(tmp){
printf("->%d",tmp->val);
tmp=tmp->next;
}
printf("\n");
}
}
int main(){
int n,x,y,w,m;
int t;
int v1,v2;
graph *tmp;
graph *var,*tmp2;
n=4;
m=4;
insert_vertex(n);
int i,j,k,l;
heap_count=n;
for(i=1;i<=n;i++){
flag[i]=0;
}
insert_heap(n);
int src,dest;
src=1;
update_heap(src,0);
while(heap_count>0){
extract_heap(heap_count);
v1=val_ans;
table[v1].weight=wt_ans;
tmp2=table[v1].next;
while(tmp2){
var=tmp2;
if(flag[var->val]==0){
v2=check_heap(var->val);
if(var->weight+table[v1].weight < v2){
update_heap(var->val,(var->weight+table[v1].weight));
}
}
tmp2=tmp2->next;
}
}
int q;
for(q=1;q<=n;q++){
printf("%d to %d = %d\n",src ,q,table[q].weight);
}
return 0;
}
C++
#include <climits>
#include <ext/pb_ds/priority_queue.hpp>
#include <iostream>
#include <utility>
#include <vector>
using namespace std;
using namespace __gnu_pbds;
template <class X, class C = greater<X>>
using heap = __gnu_pbds::priority_queue<X, C>;
vector<heap<pair<int, int>>::point_iterator> pt;
vector<int> d;
vector<vector<pair<int, int>>> g;
void dijkstra(int s) {
fill(d.begin(), d.end(), INT_MAX);
d[s] = 0;
heap<pair<int, int>> q;
pt[s] = q.push(make_pair(d[s], s));
while (!q.empty()) {
auto v = q.top().second;
q.pop();
for (auto x : g[v]) {
if (d[v] + x.second < d[x.first]) {
d[x.first] = d[v] + x.second;
if (pt[x.first] != nullptr) {
q.modify(pt[x.first], make_pair(d[x.first], x.first));
} else {
q.push(make_pair(d[x.first], x.first));
}
}
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n, m;
cin >> n >> m;
d.resize(n);
g.resize(n);
pt.resize(n);
for (int i = 0; i < m; i++) {
int x, y, w;
cin >> x >> y >> w;
// vertices must be in range [0, n)
x--;
y--;
g[x].push_back({y, w});
g[y].push_back({x, w});
}
int s;
cin >> s;
s--;
dijkstra(s);
// d[i] == INT_MAX then there is no way between s and i
for (auto x : d) cout << x << ' ';
return 0;
}
Java
/*
* To change this license header, choose License Headers in Project Properties.
* To change this template file, choose Tools | Templates
* and open the template in the editor.
*/
import java.util.ArrayDeque;
import java.util.Comparator;
import java.util.Deque;
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
import java.util.Queue;
/**
*
* @author cheikhSall
*/
public class Dijkstra {
public static class Vertex<T> {
T id;
private Map<Vertex, Integer> neighbors;
Integer cost;
public Vertex(T id) {
this.id = id;
this.neighbors = new HashMap<>();
cost = Integer.MAX_VALUE;
}
public Map<Vertex, Integer> getNeighbors() {
return neighbors;
}
public void setNeighbors(Map<Vertex, Integer> neighbors) {
this.neighbors = neighbors;
}
public Number getCost() {
return cost;
}
public void setCost(Integer cost) {
this.cost = cost;
}
public T getId() {
return id;
}
public void setId(T id) {
this.id = id;
}
public void addNeighbor(Vertex neighbor, Integer cost) {
this.neighbors.put(neighbor, cost);
}
}
public static class Graphe<T> {
private Map<T, Vertex> vertices;
public Queue<Vertex> visited;
public Deque<T> paths = new ArrayDeque<>();
public HashMap<T, Integer> distances;
public HashMap<T, T> preds;
public Graphe(Map<T, Vertex> vertices) {
this.vertices = vertices;
this.preds = new HashMap<>();
this.paths = new ArrayDeque<>();
this.distances = new HashMap<>();
this.visited = new PriorityQueue(new Comparator<Vertex>() {
@Override
public int compare(Vertex o1, Vertex o2) {
return o1.cost.compareTo(o2.cost);
}
});
}
public void initDistance() {
this.vertices.keySet().forEach((key) -> {
distances.put(key, Integer.MAX_VALUE);
this.vertices.get(key).setCost(Integer.MAX_VALUE);
});
}
public void initStart(T dep) {
initDistance();
this.distances.put(dep, 0);
}
public Integer getCurrentDistance(T id) {
return this.distances.get(id);
}
public Vertex extractMin() {
Vertex current = null;
try {
current = this.visited.remove();
} catch (Exception e) {
}
return current;
}
public Map<T, Vertex> getVertices() {
return vertices;
}
public void setVertices(Map<T, Vertex> vertices) {
this.vertices = vertices;
}
public void executeOnetoAll(T src) {
this.initStart(src);
Vertex origin = this.vertices.get(src);
if (origin != null) {
origin.setCost(0);
this.visited.add(this.vertices.get(origin.id));
while (!this.visited.isEmpty()) {
Vertex u = this.extractMin();
this.findMinimalDistancesInNeighbor(u);
}
} else {
System.out.println("vertex not existing");
}
}
public void getAllDistances() {
System.out.println("Distances : ");
this.distances.keySet().forEach((vertex) -> {
System.out.println("vertex " + vertex + " cost = " + this.distances.get(vertex).intValue());
});
}
private void findMinimalDistancesInNeighbor(Vertex u) {
u.getNeighbors().keySet().forEach((key) -> {
int cout = (int) u.getNeighbors().get(key);
Vertex v = (Vertex) key;
if (this.getCurrentDistance((T) v.id) > (this.getCurrentDistance((T) u.id) + cout)) {
this.distances.put((T) v.id, (this.getCurrentDistance((T) u.id) + cout));
v.setCost((this.getCurrentDistance((T) u.id) + cout));
this.visited.add(v);
this.preds.put((T) v.id, (T) u.id);
} else {
}
});
}
public void executeOnetoOne(T src, T goal) { // execution de l'algo sur n chemin de depart
this.executeOnetoAll(src);
Vertex origin = this.vertices.get(src);
Vertex dest = this.vertices.get(goal);
if (origin != null && dest != null) {
T step = goal;
while (origin.id != step) {
this.paths.add(step);
step = this.preds.get(step);
}
this.paths.add(src);
this.printPaths(src, goal);
} else {
System.out.println("Path not existing");
}
System.out.println();
}
public void printPaths(T src, T dest) {
System.out.println("Paths : from " + src + " to " + dest);
while (!this.paths.isEmpty()) {
System.out.print(this.paths.removeLast() + ", ");
}
System.out.println();
System.out.println("Total cost : " + this.distances.get(dest));
}
public void printGraph(){
this.vertices.keySet().forEach((key) -> {
this.vertices.get(key).getNeighbors().keySet().forEach((neighbor) -> {
Vertex v = (Vertex) neighbor;
int cost = (int) this.vertices.get(key).getNeighbors().get(neighbor);
System.out.println("("+this.vertices.get(key).id +")" +"---"+ cost+"--->"+"("+v.id+")");
});
});
System.out.println();
}
}
/**
* @param args the command line arguments
*/
public static void main(String[] args) {
Vertex<String> v1 = new Vertex<String>("A");
Vertex<String> v2 = new Vertex<String>("D");
Vertex<String> v3 = new Vertex<String>("E");
Vertex<String> v4 = new Vertex<String>("B");
Vertex<String> v5 = new Vertex<String>("F");
Vertex<String> v6 = new Vertex<String>("C");
v1.addNeighbor(v2, 2);
v1.addNeighbor(v3, 3);
v1.addNeighbor(v4, 1);
v2.addNeighbor(v1, 2);
v2.addNeighbor(v3, 3);
v2.addNeighbor(v5, 4);
v3.addNeighbor(v1, 3);
v3.addNeighbor(v2, 3);
v3.addNeighbor(v4, 8);
v3.addNeighbor(v5, 5);
v4.addNeighbor(v1, 1);
v4.addNeighbor(v6, 6);
v4.addNeighbor(v3, 8);
v5.addNeighbor(v6, 7);
v5.addNeighbor(v3, 5);
v5.addNeighbor(v2, 4);
v6.addNeighbor(v4, 6);
v6.addNeighbor(v5, 7);
Map<String, Vertex> vertices = new HashMap<String, Vertex>();
vertices.put(v1.id, v1);
vertices.put(v2.id, v2);
vertices.put(v3.id, v3);
vertices.put(v4.id, v4);
vertices.put(v5.id, v5);
vertices.put(v6.id, v6);
Graphe<String> graphe = new Graphe<String>(vertices);
System.out.println("GRAPHE :");
graphe.printGraph();
graphe.executeOnetoAll("A");
graphe.executeOnetoOne("A", "C");
graphe.getAllDistances();
graphe.executeOnetoOne("B", "F");
graphe.getAllDistances();
/* Integer entries -------------------------------------------*/
System.out.println();
Vertex< Integer> I1 = new Vertex<Integer>(1);
Vertex<Integer> I2 = new Vertex<Integer>(2);
Vertex<Integer> I3 = new Vertex<Integer>(3);
Vertex<Integer> I4 = new Vertex<Integer>(4);
Vertex<Integer> I5 = new Vertex<Integer>(5);
Vertex<Integer> I6 = new Vertex<Integer>(6);
I1.addNeighbor(I2, 2);
I1.addNeighbor(I3, 3);
I1.addNeighbor(I4, 1);
I2.addNeighbor(I1, 2);
I2.addNeighbor(I3, 3);
I2.addNeighbor(I5, 4);
I3.addNeighbor(I1, 3);
I3.addNeighbor(I2, 3);
I3.addNeighbor(I4, 8);
I3.addNeighbor(I5, 5);
I4.addNeighbor(I1, 1);
I4.addNeighbor(I6, 6);
I4.addNeighbor(I3, 8);
I5.addNeighbor(I6, 7);
I5.addNeighbor(I3, 5);
I5.addNeighbor(I2, 4);
I6.addNeighbor(I4, 6);
I6.addNeighbor(I5, 7);
Map<Integer, Vertex> vertices2 = new HashMap<Integer, Vertex>();
vertices2.put(I1.id, I1);
vertices2.put(I2.id, I2);
vertices2.put(I3.id, I3);
vertices2.put(I4.id, I4);
vertices2.put(I5.id, I5);
vertices2.put(I6.id, I6);
Graphe<Integer> graphe2 = new Graphe<Integer>(vertices2);
System.out.println("GRAPHE :");
graphe2.printGraph();
graphe2.executeOnetoAll(1);
graphe2.executeOnetoOne(4, 5);
graphe2.getAllDistances();
/**
* ** OUTPUT *****
GRAPHE :
(A)---1--->(B)
(A)---2--->(D)
(A)---3--->(E)
(B)---6--->(C)
(B)---1--->(A)
(B)---8--->(E)
(C)---6--->(B)
(C)---7--->(F)
(D)---4--->(F)
(D)---2--->(A)
(D)---3--->(E)
(E)---8--->(B)
(E)---5--->(F)
(E)---3--->(D)
(E)---3--->(A)
(F)---7--->(C)
(F)---4--->(D)
(F)---5--->(E)
Paths : from A to C
A, B, C,
Total cost : 7
Distances :
vertex A cost = 0
vertex B cost = 1
vertex C cost = 7
vertex D cost = 2
vertex E cost = 3
vertex F cost = 6
Paths : from B to F
B, A, D, F,
Total cost : 7
Distances :
vertex A cost = 1
vertex B cost = 0
vertex C cost = 6
vertex D cost = 3
vertex E cost = 4
vertex F cost = 7
GRAPHE :
(1)---3--->(3)
(1)---2--->(2)
(1)---1--->(4)
(2)---3--->(3)
(2)---4--->(5)
(2)---2--->(1)
(3)---5--->(5)
(3)---3--->(2)
(3)---8--->(4)
(3)---3--->(1)
(4)---8--->(3)
(4)---1--->(1)
(4)---6--->(6)
(5)---5--->(3)
(5)---4--->(2)
(5)---7--->(6)
(6)---7--->(5)
(6)---6--->(4)
Paths : from 4 to 5
4, 1, 2, 5,
Total cost : 7
Distances :
vertex 1 cost = 1
vertex 2 cost = 3
vertex 3 cost = 4
vertex 4 cost = 0
vertex 5 cost = 7
vertex 6 cost = 6
*/
}
}
Python
# Title: Dijkstra's Algorithm for finding single source shortest path from scratch
# Author: Shubham Malik
# References: https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
# Part of Cosmos by OpenGenus Foundation
import math
import sys
class PriorityQueue:
# Based on Min Heap
def __init__(self):
self.cur_size = 0
self.array = []
self.pos = {} # To store the pos of node in array
def isEmpty(self):
return self.cur_size == 0
def min_heapify(self, idx):
lc = self.left(idx)
rc = self.right(idx)
if lc < self.cur_size and self.array(lc)[0] < self.array(idx)[0]:
smallest = lc
else:
smallest = idx
if rc < self.cur_size and self.array(rc)[0] < self.array(smallest)[0]:
smallest = rc
if smallest != idx:
self.swap(idx, smallest)
self.min_heapify(smallest)
def insert(self, tup):
# Inserts a node into the Priority Queue
self.pos[tup[1]] = self.cur_size
self.cur_size += 1
self.array.append((sys.maxsize, tup[1]))
self.decrease_key((sys.maxsize, tup[1]), tup[0])
def extract_min(self):
# Removes and returns the min element at top of priority queue
min_node = self.array[0][1]
self.array[0] = self.array[self.cur_size - 1]
self.cur_size -= 1
self.min_heapify(1)
del self.pos[min_node]
return min_node
def left(self, i):
# returns the index of left child
return 2 * i + 1
def right(self, i):
# returns the index of right child
return 2 * i + 2
def par(self, i):
# returns the index of parent
return math.floor(i / 2)
def swap(self, i, j):
# swaps array elements at indices i and j
# update the pos{}
self.pos[self.array[i][1]] = j
self.pos[self.array[j][1]] = i
temp = self.array[i]
self.array[i] = self.array[j]
self.array[j] = temp
def decrease_key(self, tup, new_d):
idx = self.pos[tup[1]]
# assuming the new_d is atmost old_d
self.array[idx] = (new_d, tup[1])
while idx > 0 and self.array[self.par(idx)][0] > self.array[idx][0]:
self.swap(idx, self.par(idx))
idx = self.par(idx)
class Graph:
def __init__(self, num):
self.adjList = {} # To store graph: u -> (v,w)
self.num_nodes = num # Number of nodes in graph
# To store the distance from source vertex
self.dist = [0] * self.num_nodes
self.par = [-1] * self.num_nodes # To store the path
def add_edge(self, u, v, w):
# Edge going from node u to v and v to u with weight w
# u (w)-> v, v (w) -> u
# Check if u already in graph
if u in self.adjList.keys():
self.adjList[u].append((v, w))
else:
self.adjList[u] = [(v, w)]
# Assuming undirected graph
if v in self.adjList.keys():
self.adjList[v].append((u, w))
else:
self.adjList[v] = [(u, w)]
def show_graph(self):
# u -> v(w)
for u in self.adjList:
print(u, '->', ' -> '.join(str("{}({})".format(v, w))
for v, w in self.adjList[u]))
def dijkstra(self, src):
# Flush old junk values in par[]
self.par = [-1] * self.num_nodes
# src is the source node
self.dist[src] = 0
Q = PriorityQueue()
Q.insert((0, src)) # (dist from src, node)
for u in self.adjList.keys():
if u != src:
self.dist[u] = sys.maxsize # Infinity
self.par[u] = -1
while not Q.isEmpty():
u = Q.extract_min() # Returns node with the min dist from source
# Update the distance of all the neighbours of u and
# if their prev dist was INFINITY then push them in Q
for v, w in self.adjList[u]:
new_dist = self.dist[u] + w
if self.dist[v] > new_dist:
if self.dist[v] == sys.maxsize:
Q.insert((new_dist, v))
else:
Q.decrease_key((self.dist[v], v), new_dist)
self.dist[v] = new_dist
self.par[v] = u
# Show the shortest distances from src
self.show_distances(src)
def show_distances(self, src):
print("Distance from node: {}".format(src))
for u in range(self.num_nodes):
print('Node {} has distance: {}'.format(u, self.dist[u]))
def show_path(self, src, dest):
# To show the shortest path from src to dest
# WARNING: Use it *after* calling dijkstra
path = []
cost = 0
temp = dest
# Backtracking from dest to src
while self.par[temp] != -1:
path.append(temp)
if temp != src:
for v, w in self.adjList[temp]:
if v == self.par[temp]:
cost += w
break
temp = self.par[temp]
path.append(src)
path.reverse()
print('----Path to reach {} from {}----'.format(dest, src))
for u in path:
print('{}'.format(u), end=' ')
if u != dest:
print('-> ', end='')
print('\nTotal cost of path: ', cost)
if __name__ == '__main__':
graph = Graph(9)
graph.add_edge(0, 1, 4)
graph.add_edge(0, 7, 8)
graph.add_edge(1, 2, 8)
graph.add_edge(1, 7, 11)
graph.add_edge(2, 3, 7)
graph.add_edge(2, 8, 2)
graph.add_edge(2, 5, 4)
graph.add_edge(3, 4, 9)
graph.add_edge(3, 5, 14)
graph.add_edge(4, 5, 10)
graph.add_edge(5, 6, 2)
graph.add_edge(6, 7, 1)
graph.add_edge(6, 8, 6)
graph.add_edge(7, 8, 7)
graph.show_graph()
graph.dijkstra(0)
graph.show_path(0, 4)
# OUTPUT
# 0 -> 1(4) -> 7(8)
# 1 -> 0(4) -> 2(8) -> 7(11)
# 7 -> 0(8) -> 1(11) -> 6(1) -> 8(7)
# 2 -> 1(8) -> 3(7) -> 8(2) -> 5(4)
# 3 -> 2(7) -> 4(9) -> 5(14)
# 8 -> 2(2) -> 6(6) -> 7(7)
# 5 -> 2(4) -> 3(14) -> 4(10) -> 6(2)
# 4 -> 3(9) -> 5(10)
# 6 -> 5(2) -> 7(1) -> 8(6)
# Distance from node: 0
# Node 0 has distance: 0
# Node 1 has distance: 4
# Node 2 has distance: 12
# Node 3 has distance: 19
# Node 4 has distance: 21
# Node 5 has distance: 11
# Node 6 has distance: 9
# Node 7 has distance: 8
# Node 8 has distance: 14
# ----Path to reach 4 from 0----
# 0 -> 7 -> 6 -> 5 -> 4
# Total cost of path: 21
Applications
-
Telephone network: In a telephone network the lines have bandwidth, BW. We want to route the phone call via the highest BW.
-
Flight: A travel agent requests software for making an agenda of flights for clients. The agent has access to a data base with all airports and flights. Besides the flight number, origin airport and destination, the flights have departure and arrival time. Specifically the agent wants to determine the earliest arrival time for the destination given an origin airport and start time.
-
File Server: We want to designate a file server in a local area network. Now, we consider that most of time transmitting files from one computer to another computer is the connect time. So we want to minimize the number of “hops” from the file server to every other computer on the network.
