In this article, we will understand What is ReLU? and What do we mean by “Dying ReLU Problem” and what causes it along with measures to solve the problem.

Table of Contents:

1. Introduction
2. What are (Artificial) Neural Networks?
3. What are Activation Functions in Neural Networks?
4. What is ReLU?
5. What is Dying ReLU?
6. What causes a Dying ReLU Problem?
7. How to solve Dying ReLU Problem?

Introduction:

Rectified Linear Unit i.e. ReLU is an activation function in Neural Network. Hahnloser et al. first proposed it in 2000. Deep neural networks, computer vision, and speech recognition all make use of it.

Before moving on to the main topic of the article, if you don’t know what are Neural Networks and what are activation functions in neural network, let me explain it to you in short.

What are (Artificial) Neural Networks?

(Artificial) Neural Networks are a part of Deep Learning Algorithms. Their name and structure are derived from the human brain, and they resemble the way real neurons communicate with one another.

A Neural Network comprises of node layers, which contain an input layer, hidden layers, and an output layer. In the domains of AI, machine learning, and deep learning, neural networks mimic the function of the human brain, allowing computer programmes to spot patterns and solve common problems.

Let's look at the structure of a Neural Network:

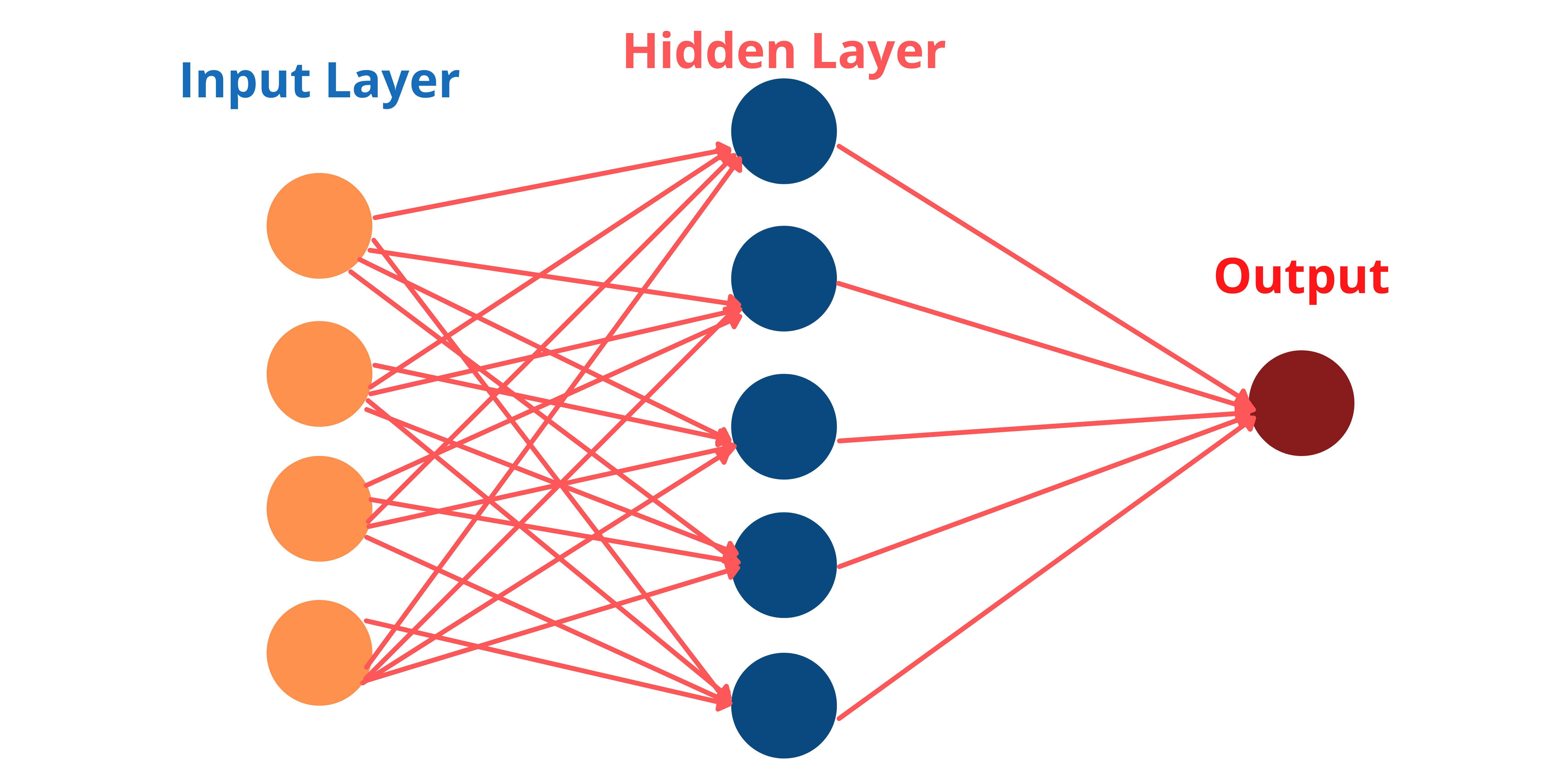
What are Activation Functions in Neural Networks?

Activation Function also called as transfer functions are equations that define how the weighted sum of the input of a neural node is transformed into an output.

Basically, an activation function is just a simple function that changes its inputs into outputs with a defined range. The sigmoid activation function, for example, receives input and translates the output values between 0 and 1 in a variety of ways.

The output signal becomes a simple linear function if the activation function is not used. Without an activation function, a neural network will behave like a linear regression with minimal learning potential.

Now, this brings us to our main question/topic of the Article i.e. What is ReLU and What is ‘Dying ReLU problem’?

What is ReLU?

As mentioned earlier, Rectified Linear Unit also called as ReLU is an activation function in Neural Network which are majorly used in computer vision, speech recognition etc.

Mathematically it is represented by:

f(x)=max(0,x)

So, now since we know that Rectified Linear Unit is a form of activation function, what does it do? The rectified linear activation function, is a real-valued function that outputs the input directly if it is positive and 0 if it’s negative.

Since it is quicker to train and delivers superior results, it has become the default activation function for many types of neural networks. The vanishing gradient problem is solved with the rectified linear activation function, allowing models to train quicker and perform better.

Advantages of ReLU:

• When compared to tanh and sigmoid, ReLU uses simpler mathematical procedures, which improves its computing speed even more.
• ReLU requires less time to learn and is less complicated to calculate than other common activation functions (tanh, sigmoid, etc.). As explained if the input is negative, it will output 0, which will activate fewer neurons, that will lead to network sparsity, and improve computational efficiency.
• One significant advantage is that the gradient is less likely to vanish.
• Networks with ReLU tend to show better convergence performance than sigmoid (another activation Function).

So, now let’s address the main topic “Dying ReLU”

What is Dying ReLU?

The dying ReLU is problem when the neurons become inactive and output only 0 values basically negative values. This most probably occurs by learning a significant negative bias term for its weights.

The moment the ReLU ends up in this state, it cannot recover, since the function gradient at 0 is also 0. When the sigmoid and tanh neurons' values saturate, they can have comparable/similar problems, but there is always a modest gradient that allows them to recover in the long run.

Let’s understand why ReLU cannot recover by an example:

Let’s say there is a Artificial Neural Network which has some distribution over it’s input X. Now, let’s focus on a particular ReLU unit R. Whenever there are fixed set of parameters the distribution over X implies distribution over the inputs R. Assume R's inputs are distributed as a low-variance Gaussian centered at +0.1.

For this scenario:

• The majority of R's inputs are positive.
• The ReLU gate will be open for the majority of inputs.
• The majority of inputs will cause gradients in R to flow backwards.

SGD backprop is commonly used to update R's inputs.

Now, assume that a big magnitude gradient is transferred backwards to R during a particular backprop. R will transfer this huge gradient backwards to its inputs because it is open. This results in a significant change in the function that computes R's input. This means that the distribution of R's inputs has changed; for example, assume that R's inputs are now distributed as a low-variance Gaussian centred at -0.1.

For this scenario:

• The majority of R's inputs are negative.
• The majority of inputs will cause the ReLU gates to be closed
• The inputs will cause the gradients to fail and to flow backwards through R

As a result, the R’s inputs will not be updated by SGD backdrop.

So, basically R's behavior has changed qualitatively as a result of a relatively slight change in its input distribution. We've passed the zero line, and R is virtually always closed now. The difficulty is that a closed ReLU can't change its input parameters, therefore it stays dead.

So, to sum it up, The gradients fail to flow during backpropagation when the majority of these neurons return output zero, and the weights are not updated. Eventually, a big portion of the network goes dormant, and it is unable to learn anything new. So, the ReLU neuron is dead if it is stuck in the negative side and everytime it outputs zero.

Now, lets understand what causes it?

What causes a Dying ReLU Problem?

The causes are divided into these 2 factors:

1. Large Negative Bias
2. High Learning Rate

1. Large Negative Bias:

Let's start with an explanation of what a bias is. A bias is a constant value that is added to the sum of the inputs and outputs. Now, a large negative bias can make the ReLU activation inputs to become negative. As mentioned earlier, a negative input will output 0, which will lead to the dying ReLU problem.

2. High Learning Rate:

Because our old weights will be subtracted by a huge number if our learning rate () is set too high, there is a good probability that our new weights will end up in the severely negative value range. Negative weights result in negative ReLU inputs, resulting in the dying ReLU problem.

How to solve the Dying ReLU problem?

1. You could set your bias weight to a positive number at the start.
2. You could use a lower learning rate during the training process
3. Make the use of Leaky ReLU, which is a common and a pretty effective method for solving the dying ReLU problem.