
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will explore the fascinating concept of Egyptian Fractions and will learn what they are and will also see an example of how they can be solved using greedy algorithm techniques.
What is Egyptian Fraction?
Egyptian fraction is the representation of any fraction into sum of unit fractions. A unit fraction is one which has unit numerator .These epresentations were first used in ancient Egypt but the first published greedy algorihm method to convert the rational numbers(which can't be reduced further) into Egyptian Fraction was first described by Fibonacci.
For e.g:- 15/56 = (1/7)+(1/8).
A greedy algorithm is the one in which we either need to choose some kind of maximum or minimum at every stage for our solution.
In the algorithm for Egyptian Fraction, we need to find the maximum possible unit fraction which can be used for the remaining fraction and hence this method of finding the representation is called the Egyptian fraction, and is also an example of a greedy method.
Any rational number can have infinitely many representation of Egyptian Fractions, although the number of representation having given number of terms is finite. However, the egyptian fraction profuced by the greedy algorithm may not be the shortest Egyptian Fraction.
Mathematical Formula for Egyptian Fractions
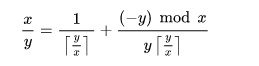
where ⌈ ⌉ represents the ceiling function;
and also, since (−y) mod x < x, this method yields a finite expansion, and we should continue iterating till we get to our desired representation of unit fractions.
Algorithm of Egyptian Fractions
In this algorithm we try to extract the largest unit fraction and first and then do the same for the remaining fraction iteratively till we get our desired representation.
For a fraction, m/n, 1/(⌈n/m⌉) is the largest unit fraction.
For example for 3/5 , 1/(⌈5/3⌉) i.e. 1/2 is the largest unit fraction which can be extracted .
Once, 1/2 is extracted from 3/5 we are left with 3/5 - 1/2 = 1/10.
Thus, we have got our desired representation of unit fraction in just 2 steps. i.e. 3/5 = 1/2 +1/10.
Let us take another example involving more steps for more clarity:-
Take the number 521/1050, we need to represent it into the sum of unit fractions.
Again, using the method of extracting the largest unit fraction from the function, we get 1/(⌈1050/521⌉) = 1/3.
Now, the remaining fraction is 521/1050 -1/3 =57/350.
Again, applying the same step for the 57/350 i.e. extracting the largest unit fraction from 57/350 we get 1/(⌈350/57⌉), i.e. 1/7.
Now, the remaining fraction is 57/350 -1/7 = 1/50.
Thus, 521/1050 = 1/3 + 1/7 + 1/50.
Had we did not get what we wanted then we would have continued to extract the largest unit fraction from the remaining fraction till the remaining fraction is itself a unit fraction,
Algorithmic steps to find Egyptian Fractions
Let us give this algorithm a structured look:-
- Extract the largest unit faction from the given fraction.(For a fraction (m/n), 1/(⌈n/m⌉) is the largest unit fraction which can be extracted).
- Calculate the remaining fraction(i.e. subtract the extracted fraction from the original fraction).
- If the remaining fraction is a unit fraction then you are done.
- Else, apply step 1st to 3rd iteratively over that remaining fraction.
- Represent your original fraction as sum of all those largest unit fractions extracted to get egyptian fraction of that fraction.
Implementation Of Egyptian Fractions.
Following is the implementation in C++:
#include <iostream>
using namespace std;
void Egyptian_fraction(int numerator, int denominator)
{
// If denominator divides numerator then that number is not a fraction and hence, Egyptian Fraction is not possible.
if (numerator%denominator == 0)
{
cout<<numerator/denominator<<" Egyptian fraction of an integer is not possible";
}
// when numerators and denominators are zero.
else if (denominator == 0 || numerator == 0)
{
cout<<"No representation possible as either the numerator or the denominaor is zero, while egyptian fraction can only be calculated for fractions.";
}
// If numerator less than denominator and denominator%numerator=0 , then simple division will result in the unit fraction.
else if (denominator%numerator == 0)
{
cout<<"1/"<<denominator/numerator;
}
// When Numerator > Denominator
else if (numerator > denominator)
{
cout<<numerator/denominator<<" + ";
Egyptian_fraction(numerator%denominator, denominator);
}
// If given proper values i.e. denominator > numerator and denominator%numerator is non-zero,then Find ceiling of denominator/numerator, and recursively
//call the Egyptian_fraction for the remaining part.
else
{
int ceiling_value;
ceiling_value = (int)denominator/numerator + 1; //This will return the celing values as denominator/numerator will be an integer.
cout<<"1/"<<ceiling_value<<" + ";
//Remaining fraction= Numerator/ Denominator- 1/ ceiling_value = (Numerator*ceiling_value - Denominator)/Denominator*ceiling_value.
Egyptian_fraction(numerator*ceiling_value-denominator, denominator*ceiling_value);
}
}
int main()
{
int numerator, denominator;
//Entering the values for our fraction.
cout<<"Enter the numerator value for the fraction";
cin>>numerator;
cout<<"Enter the denominator value for the fraction";
cin>>denominator;
cout<<"Egyptian Fraction Representation of "<<numerator<<"/"<<denominator<<" is\n ";
// Calling the function for the representtion of our fraction.
Egyptian_fraction(numerator, denominator);
return 0;
}
Complexity of the Code
Let n be the number of times the function iterates which can't be found beforehand, thus, it is a recursive funtion of type
T(n)=T(n-1)+k. (where 'k'is some constant).
Its time complexity is O(n)
Space complexity is O(1), as it always allocates the same space no matter what the output is.
Applications of Egyptian Fractions
It can be used when we need to have as fewer partitons as possible while dividing things eually, among certain number of people.
For example:- Suppose we want to divide 5 sweets into 8 people by making as fewer partitions as possible then, we can use Egyptian Fraction of 5/8 which will be ((1/2)+(1/8)), which can also be represented as (4/8)+(1/8), which can be interpreted as dividing four sweets into 8 eequal halves and then doing 8 parts of the remaining sweet. Thus, we just had to 16 partitions while in the conventional method we would have divided each sweet into 8 divisions, which would have amounted to 40 partitions.
Electronic circuit design is another area where Egyptian fractions have practical use, i.e. finding the combinations of what electrical resistors are needed to be added in parallel to get a particular value of rsistance acros the wire.
Since, 1/R = 1/R1 + 1/R2 + 1/R3 and so on.
which can be solved using similar technique as used in greedy algorithm of Egyptian Fraction, and is exactly same as the Egyptian fraction if 1/R is not a unit fraction.
Question
Question
You have to divide 11 breads into 12 people, find the least number of partitions reqquired to divide these 11 breads into 12 people equally.
With this article at OpenGenus, you must have the complete idea of Egyptian Fractions.
