Feature Selector Using LASSO

A technique for reducing the dimensionality of machine learning datasets is the Feature Selector. The selection process of the Feature Selector is based on a logically accurate measurement that determines the importance of each feature present in the data. In this article at OpenGenus, we explore the advantage of a Feature Selector built using the principles of LASSO over a conventional method.

Table of contents

1. Introduction
2. Implementation
3. Observations

Introduction

According to Wikipedia, The combination of a search method for suggesting new feature subsets and an assessment metric that ranks the various feature subsets is what is known as a feature selection algorithm. The simplest approach is testing each potential feature subset to see which one has the lowest error rate. For all but the smallest feature sets, this is an exhaustive search of the available space and is computationally intractable. The three major types of feature selection algorithms may be distinguished by the evaluation metrics that are used, and these evaluation metrics have a significant impact on the algorithm. filter, embedded methods, and wrappers.

The advantages of performing feature selection are,

1. enhance data's suitability for a class of learning models.
2. Inherent symmetries in the input space are encoded.
3. less training sessions.
4. model simplification to facilitate better interpretation

Additional Details on LASSO solution and its use can be found Here

The approach going to be followed for implementing both the Feature selection operations are as follows,

1. Non-Lasso Implementation (Conventional data analysis),

1. Manually calculating the correlation values of each feature of the data vs to the result.
2. Take the absolute of the value obtained for each correlation, this is done because high correlation and anti-correlation
   both are important contributors to the predictions of the model.
3. Sort the absolute correlation features in descending order(Highest to lowest order).

2. LASSO implementation,

1. Use the LASSO model to select the important features.
2. Sort the correlations selected features in descending order(Highest to lowest order).

Implementation

The required packages for this experiment can be imported by,

import numpy as np
import scipy.stats
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import Lasso

following this we will use any one of sklearn's toy datasets to perform the feature selection, the Boston Dataset for example can be imported by,

from sklearn.datasets import load_boston
X,y = load_boston(return_X_y=True)
features = load_boston()['feature_names']

Other similar datasets that you may choose to use can be found Here

The Next step would be to create a Train Test split among the dataset, which can be done as so,

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

Following this, we will create a pipeline for scaling,

pipeline = Pipeline([ ('scaler',StandardScaler()), ('model',Lasso()) ])

Finally, we can begin searching, here we are going to test several values from 0.1 to 10 with 0.1 steps. For each value, we calculate the average value of the mean squared error in a 5-folds cross-validation and select the value of α that minimizes such average performance metrics.

search = GridSearchCV(pipeline, {'model__alpha':np.arange(0.1,10,0.1)}, cv = 5, scoring="neg_mean_squared_error",verbose=3)

In the above code section, we used neg_mean_squared_error because the grid search tries to maximize the performance metrics, so we add a minus sign to minimize the mean squared error.

Next, we train the model,

search.fit(X_train,y_train)

After training, we can acquire the best value for α using,

best_alhpa = search.best_params_
print("Best value for alpha is = ", '%.6f'%float(best_alhpa['model__alpha']))

Now, we have to get the values of the coefficients of Lasso regression. The importance of a feature is the absolute value of its coefficient,

coefficients = search.best_estimator_.named_steps['model'].coef_
importance = np.abs(coefficients)
print(importance)

We set a threshold value to allow us to control the level of impactfulness required from the features,

threshold = 0

According to the set threshold,

The features that survived the Lasso regression can be found by,

np.array(features)[importance > threshold]

similarly, The features that did not survive the Lasso regression are,

np.array(features)[importance <= threshold]

This completes the LASSO implementation now we will implement the correlation-based method on the same data,

r_col = y_train
n_ft = len(X_train[0])
n_cof = [None]*n_ft

for i in range(n_ft):
    i_col = df = X_train[:,i]
    n_cof[i] = scipy.stats.pearsonr(r_col, i_col)[0]

importance_corr = np.abs(np.round(n_cof,4))

print(importance_corr)

next, we will select a small number to check if the most significant is always being selected,

! Note this part may differ for different datasets based on the features being used. trail and error should work fine for small datasets.

n_imp = 5

Next, we can find the highest impactful features wrt correlation coefficient values by,

print(np.sort(importance_corr)[::-1][:n_imp])

Now we can compare both the selected features using,

imp_arr = importance_corr*[importance > threshold]
rel_imp = imp_arr[np.nonzero(imp_arr)]

print(np.sort(importance_corr)[::-1][:n_imp])

print(np.sort(rel_imp)[::-1][:n_imp])

Observations

On running the same code for 4 common different toy datasets(Boston, Wine, Digits, and Iris) we obtained the following output,

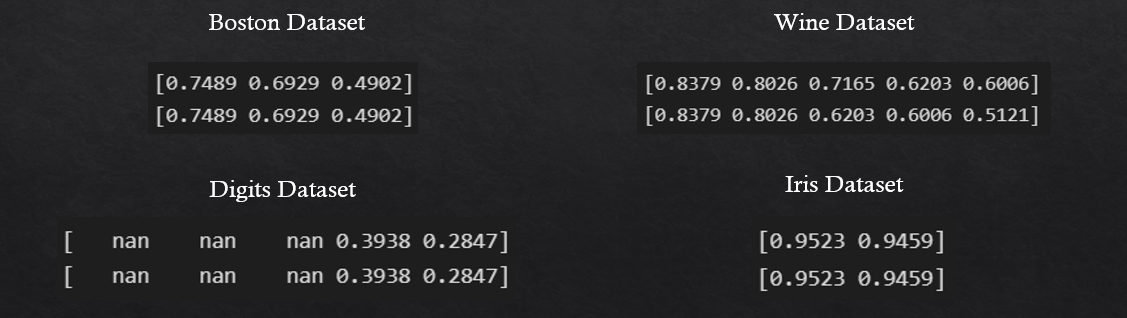
When manually calculating the highest absolute correlation among all features concerning the result for feature selection
we are considering the most important features. Hence, when both the implementation results are nearly identical from this
we can infer, that the LASSO model is indeed correctly selecting the most important features.

The main advantage of The LASSO-based Feature selector is that it is scaleable to datasets with a large number of features whereas the manual implementation would be computationally expensive and tedious.