In this article, we will talk about a relatively new activation function and somewhat better as well. Basically we will be discussing about Gaussian Error Linear Unit or GeLU.

Table of Contents:

1. Introduction.
2. Gaussian Error Linear Unit.
3. Differences Between major Activation Functions and GelU.
4. Experimenting GeLU on MNIST.
5. Experimenting GeLU on CIFAR-10.
6. Summary.

Pre-requisites:

• Types of Activation Functions used in Machine Learning
• Swish Activation Function

Introduction

For neural networks, the sigmoid function was previously the most used nonlinear activation function. It has gone out of favour due to delayed and imprecise convergence, despite having a probabilistic interpretation. The commonly utilised ReLU activation, on the other hand, frequently exhibits higher convergence but lacks a probabilistic interpretation. Despite their differences, both nonlinearities can have a significant influence on a neural network's overall performance.

ReLUs lack stochasticity and since the aforementioned regularizers are irrespective of their input, the innovations have remained distinct even though each uses zero or identity maps. To bridge the gap between nonlinearities and stochastic regularizers by considering a new stochastic regularizer that is dependent upon input values. we encapsulate the stochastic regularizer into a deterministic activation function that we call the Gaussian Error Linear Unit (GELU). GELU activations outperform both ReLU and ELU activations.

Gaussian Error Linear Unit

The Gaussian Error Linear Unit, or GeLU, is a function that simply multiplies its input by the cumulative density function of the normal distribution at this input. Because this computation is rather slow, a considerably quicker approximation that varies only in the fourth decimal place is frequently employed in practise.

Implementation:

from scipy.stats import norm

def gelu(x):
    return x*norm.cdf(x)
def gelu_approx(x):
    return .5 * x * 1(1 + tanh(np.sqrt(2/np.pi)*(x+0.044715 * x**3))

GELU, unlike the ReLU family of activations, weights its inputs by their value rather than their sign when thresholding. When GELU activation is compared to the ReLU and ELU functions, it has been discovered that GELU activation improves performance across all computer vision, natural language processing, and voice tasks.

Since the cumulative distribution function of a Gaussian is often computed with the error function, we define the Gaussian Error Linear Unit (GELU) as:

GELU(x) = xP(X ≤ x) = xΦ(x) = x · 1 2 h 1 + erf(x/√ 2)i . 

We can approximate the GELU with:

0.5x(1 + tanh[p 2/π(x + 0.044715x 3 )]) 

or

xσ(1.702x)

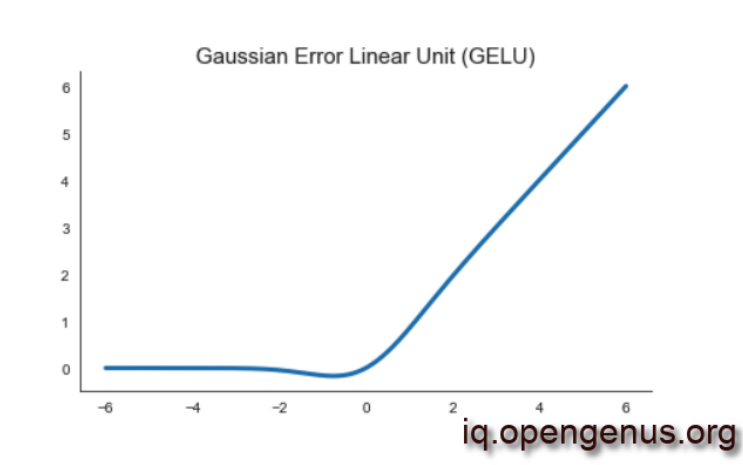
The GELU looks a lot like the ReLU and ELU. The GELU, for example, becomes a ReLU when σ→0 and μ=0. Furthermore, the ReLU and GELU are asymptotically equivalent. The key difference between GelU and ReLu is that, unlike ReLU, GeLU may be both negative and positive.

Let's talk more about the differences.

Differences Between the major Activation Function and GeLU:

• There are a few major distinctions in the GELU. In the positive domain, this non-convex, non-monotonic function is not linear and has curvature at all locations.
• Meanwhile, convex and monotonic activations such as ReLUs and ELUs are linear in the positive domain and so lack curvature.
• As a result, GELUs may be able to approximate difficult functions more readily than ReLUs or ELUs due to their greater curvature and non-monotonicity.
• Furthermore, because it is the predicted SOI map, which incorporates notions from dropout and zoneout, the GELU has a probabilistic meaning.

Experimenting GeLU on MNIST:

MNIST classification:

We evaluate the GELU, ReLU, and ELU on MNIST classification (grayscale images with 10 classes, 60k training examples and 10k test examples)

Let's see if this nonlinearity has any effect on past activation functions. To do this, we use GELUs (=0,=1), ReLUs, and ELUs (=1) to train a fully connected neural network. With a batch size of 128 neurons, each 7-layer, 128 neuron wide neural network is trained for 50 epochs. We employ the Adam optimizer, which recommends a learning rate of 0.001. The weights are equally started on the unit hypersphere since this improves the performance of each nonlinearity. Finally, we accomplish this job with no dropouts and a 0.5 dropout rate. Under both dropout rates, the GELU has the lowest median training log loss, as shown in Figure 2. As a result, while being inspired by a distinct stochastic process, the GELU works well with dropout.

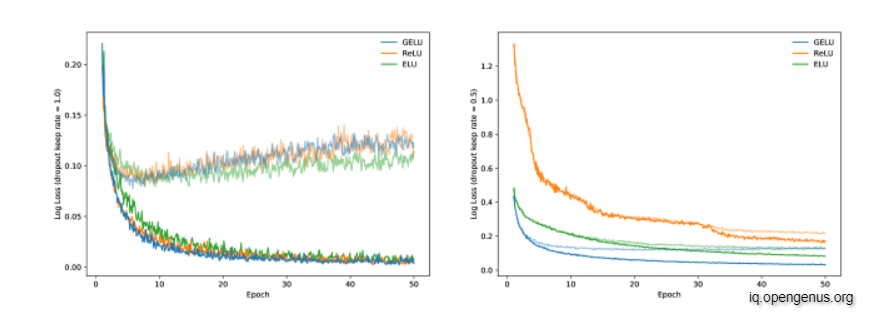
Figure: MNIST Classification Results. Left are the loss curves without dropout, and right are curves with a dropout rate of 0.5. Each curve is the the median of five runs. Training set log losses are the darker, lower curves, and the fainter, upper curves are the validation set log loss curves.

MNIST AUTOENCODER:

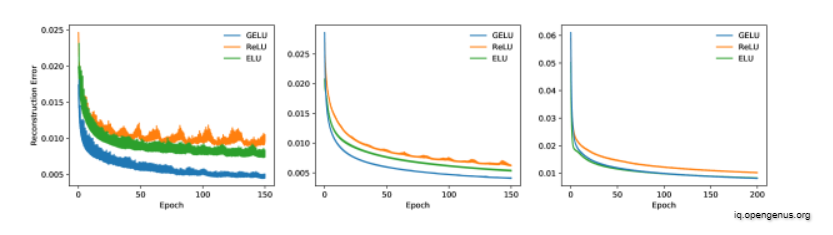
We'll now train a deep autoencoder on MNIST in a self-supervised scenario. We utilise a network with layers with widths of 1000, 500, 250, 30, 250, 500, 1000, in that sequence, to achieve this. We employ the Adam optimizer with a batch size of 64 once again. The mean squared loss is what we have. The learning rate varies from 103 to 105. The outcomes are depicted in Figure. The GELU ties or outperforms the other nonlinearities considerably. This demonstrates that the GELU nonlinearity is stable and accurate at various learning rates.

Experimenting GeLU on CIFAR-10:

CIFAR-10 classification (color images with 10 classes, 50k training examples and 10k test examples) tasks.

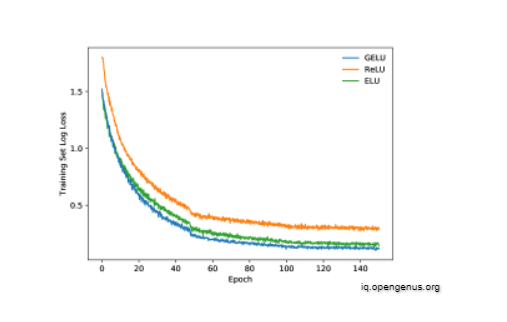
For more intricate architectures the GELU nonlinearity again outperforms other nonlinearities. Using the CIFAR-10 dataset, we evaluate this activation function on shallow and deep convolutional neural networks. With a shallow architecture, the network has the stacks (2×3×32),(2×3×64) representing the number of layers, receptive field, and number of filters, respectively. Then feed this output through a two layer network with 512 and 256 neurons for the two layers. We apply max-pooling after every stack, and we run two experiments: we apply no dropout or use dropout rates of 0.25 after the first stack, 0.25 after the second stack, and 0.5 before the last fully-connected layer. We use the Adam optimizer, tune over the learning rates 10−3,10−4,10−5, and initialize weights on the unit hypersphere (each filter has an ℓ2 norm of one). Figure shows the results. In both situations, GELUs provide faster and superior convergence.

Summary:

Pros:

• It appears to be cutting-edge in NLP, particularly for Transformer models that is, it outperforms the competition.
• Avoids the problem of vanishing gradients

Cons:

• Although it was launched in 2016, it is still relatively new in practical application.

With this article at OpenGenus, you must have the complete idea of Gaussian Error Linear Unit (GELU).