Area of Triangle: Heron's formula

Reading time: 30 minutes | Coding time: 15 minutes

In this article, we will take a look at Heron's formula which will enable us to calculate the area of any triangle given the length of the three sides of that triangle. The advantage is that the area is calculated using arithmetic operations and hence, the time taken can be assumed to be constant,

Heron's formula named after Hero of Alexandria.

Different approaches

There are 7 common ways in which the area of a triangle is calculated. Following are some of the ways:

Consider the following image demonstrating the various measurements of a triangle:

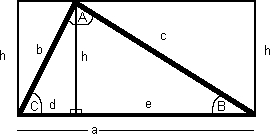
1. Area = (a * h) / 2
2. Area = (a * b * sin(C)) / 2
3. Area = (a2 * sin(B) * sin(C)) / (2 * sin(B + C))

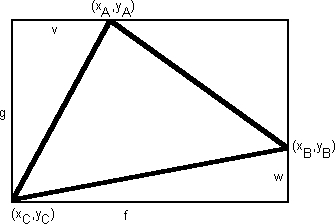
Consider the following image demonstrating the various measurements of a triangle:

4. Area = f * (g / 2) - v * (w / 2)
5. Area = abs(((xB * yA) - (xA * yB))+((xC * yB) - (xB * yC)) + ((xA * yC) - (xC * yA))) / 2

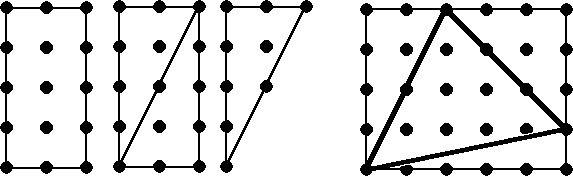
Consider the following image demonstrating the various measurements of a triangle:

6. If the vertices are at integer points on a grid of points then area of triangle is given by :
   Area = number of points inside triangle + half number of points on edge of triangle - 1

7. Using Heron's Formula.

Formula

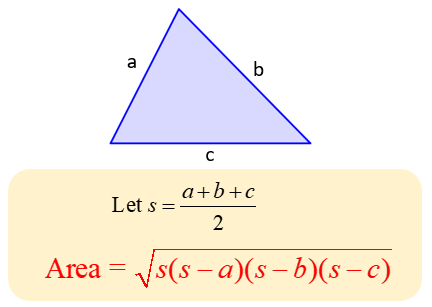
where s is the semi-perimeter of the triangle.

Algorithm

• step 1: Accept the length of sides of triangle.
• step 2: Let magnitude of sides of triangle be a, b, and c. Calculate the semi-perimeter of trinagle i.e : s

Formula : s = (a + b + c) / 2

• step 3: To calculate Area of Triangle apply Hero's Formula :

Formula : Area = sqrt( s * (s-a) * (s-b) * (s-c))

• step 4: Exit.

Implementation

#include <iostream>
#include <cmath>

class AreaOfTriangle
{

public:

    AreaOfTriangle(double a, double b, double c) : a_(a), b_(b), c_(c) { }

    double calculateArea();

private:
    double a_, b_, c_;

};

double AreaOfTriangle::calculateArea()
{
    /*
     * As magnitude of length of sides must be positive.
     * Given length of sides of triangle must follow the following result :
     * "Sum of any two sides of triangle must be smaller than the third side of triangle".
     */
    if (a_ < 0 || b_ < 0 || c_ < 0 || a_+b_ <= c_ || a_+c_ <= b_ || b_+c_ <= a_)
        return 0.0;
    double s = (a_ + b_ + c_) / 2; //semi-perimeter of triangle
    return sqrt(s * (s - a_) * (s - b_) * (s - c_));
}

int main()
{
    double ta, tb, tc;
    std::cout << "\nEnter the length of side-1 : ";
    std::cin >> ta;
    std::cout << "\nEnter the length of side-2 : ";
    std::cin >> tb;
    std::cout << "\nEnter the length of side-3 : ";
    std::cin >> tc;
    AreaOfTriangle a(ta, tb, tc);
    if(a.calculateArea() == 0.0)
        std::cout << "\nInvalid Triangle";
    else
        std::cout << "\nArea of Triangle : " << a.calculateArea() << " square units.";

}

Example

Input : a = 5.0, b = 7.0, c = 9.0

step 1 : calculate semi-perimeter, s = (a + b + c)/2
s = (5.0 + 7.0 + 9.0) / 2
= (21) / 2
= 10.5

step 2 : calculate Area of triangle = (s * (s - a_) * (s - b_) * (s - c_)
= 10.5 * (10.5 - 5.0) * (10.5 - 7.0) * (10.5 - 9.0)
= 303.1875
= sqrt(303.1875)
= 17.412280149

Output : Area of Triangle : 17.412280149 square units.

Complexity

The time and space complexity to calculate Area of Triangle are:

Assuming arithmetic operations (like multiplication and square root) take constant time O(1):

• Worst case time complexity: Θ(1)
• Average case time complexity: Θ(1))
• Best case time complexity: Θ(1)
• Space complexity: Θ(1)

Actual time complexity:

Considering numeric input N and multiplication takes O((log(N))^2) time:

• Worst case time complexity: Θ((log(N))^2)
• Average case time complexity: Θ((log(N))^2)
• Best case time complexity: Θ((log(N))^2)
• Space complexity: Θ(1)

A number N has log(N) digits and the most common way of multiplication takes O(D^2) time complexity where D is the number of digits = log N.

Square root is usually calculated using Newton's method which takes the same complexity as that of the multiplication algorithm used. Hence, the overall time complexity of the Heron's method is O((log(N))^2)

Further Reading

• Area of Polygon