Research question: How can CNNs be speed up?

Approaches to speed up CNNs

They can be sped up by using 3 approaches:

(a) unrolling convolution
(b) using BLAS (basic linear algebra subroutines)
(c) using GPUs (graphic processing units).

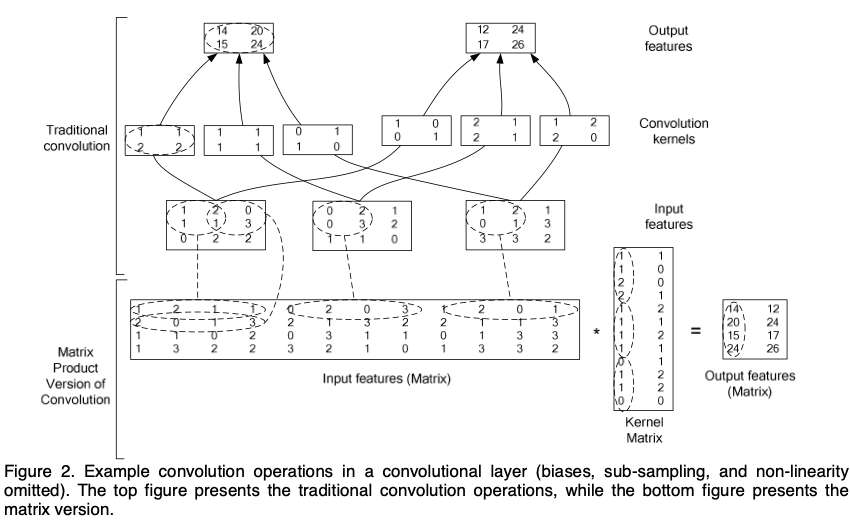
Unrolling convolution converts the processing, including both forward and backward propagation, in each convolutional layer, to a matrix-matrix product. With this matrix-matrix product representation, the implementation is as easp as MLPs.

BLAS (basic linear algebra subroutines) is used to compute matrix productws on the CPU.

A pixel shader based GPU implementation CNNS were also produced.

We have explored the paper "High Performance Convolutional Neural Networks for Document Processing" by Kumar Chellapilla, Sidd Puri and Patrice Simard affiliated by Microsoft Research.

Experiment

Conducted with two character recognition problems, using 10 (MNIST) and 94 (Latin) classes.

MNIST:60000 handwritten digits, uniformly distributed over 0-9
Latin: 94 most common ASCII characters in the English language

Results

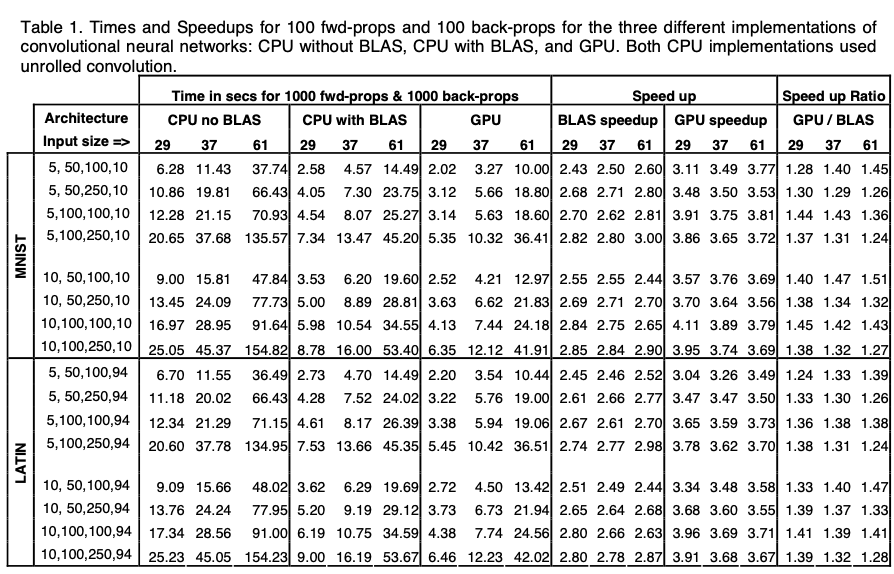
These approaches were used to tackle character recognition problems. Test error rates were under 1.2%I across the training networks, and the speedups observed were fairly consistent over different network sizes and between two implemntations - however, faster speedups were observed on larger network sizes.

'In using unrolled convolution with BLAS (1 and 2), there was a 2.4X-3.0X speedup for both problems and all input sizes - there was no speedup without BLAS, or when vectors had less than 65 floats in their row/column. As for the GPU implementation, a 3.1X-4.1X speedup was produced.

The wall clock training times are presented below.

Implications

It is likely that further dramatic speedups will be observed thanks to current trends towards multicore CPU/GPUs with multiple pipelines.

Background

Comparison of CNNs to NNs

A Convolutional Neural Network (CNN) is well suited to self visual document tasks that rely on recognition and classification. They are comprised of layers of convolutional notes followed by layers of fully connected nodes. An example is shown below for handwritten digit recognition. In the example, the weights or free parameters are shared into layers. Less than 5% of the weights in the whole CNN are used in the convolutional layers (6430 of 133780). Although the CNN is similar in size to a regular two layered neural network in terms of memory and capacity, convolutional operations are computationally more expensive. They require 67% more time and are 3X slower than their fully connected equivalents.

When compared to neural networks (NNs) they are more simple to build and use. Furthermore, CNNs are more flexible in terms of architecture and are generally simple to use, as they do not require considerations such as momentum, weight decay or structure dependent learning rate. Using a CNN is also appropriate as they excel at character recognition, as shown on MNIST data set of hand written English digital images.

Three sources make up the computational complexity of the convolution layers: first, the convolution operation; second, small kernel sizes; and finally cache unfriendly memory access.

1 Convolution operation

In a convolutional node, the number of operations per input grows quadratically with the length of the kernel.

2 Small kernel sizes

Typical kernel sizes range from 3×3 to 9×9, they are formed from four nested loops, and the small kernel sizes affect the inner loops by making them very inefficient as they frequently encourage JMP instructions.

3 Cache unfriendly memory access

Forward and backward propagation steps require both row-wise and column-wise data from the input and kernel images. As 2D images are often represented in a row-wise-serialised order, column-wise access results in a higher rate of cache misses in the memory subsystem.

Weight Sharing technique

When processing large input images through sequential scanning, the weight-sharing technique has an interesting computation sharing property - as convolutions can directly be performed on larger imports instead of performing convolutions on single characters, it is much more economical time-wise when whole words or lines of texts are processed in a batch. Space Displacement Neural Networks (SDNN) are used to refer to multiple input, multiple output CNN.

More information on each approach

1 Unrolling convolutional layers

Mini-problem: straight-forward implementation of convolution is not well suited for fast execution on modern computers
Solution: Reorganisation and duplication of the convolution inputs to fit CPU requirements, so that special parallel hardware (e.g. SSE, MMX) can be used to speed up convolution
Summary: Input is unfolded and duplicated, kernel parameters are rearranged, leading to a CPU friendly ordering. Each convolutional layer is converted to a matrix product during forward propagation. A further advantage is the back-propagation step can be written as another matrix product.
Other applications: signal processing, communications matrices

The matrix product version of the convolutional layer is shown in the figure below. Rewriting: all the input values necessary to compute one element of an output feature are in each row - this implies duplication as well.

The general version of the unrolled convolution layer with O_f nodes is shown in the figure below.

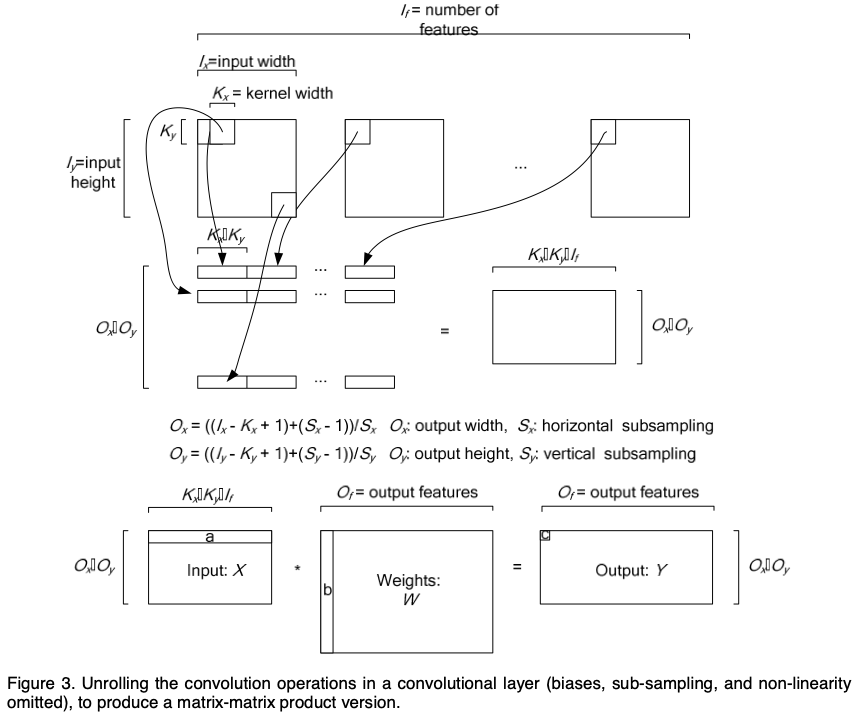
The equations corresponding to this for froward-propagation, back-propagation and weight updates are shown below.

Basic linear algebra subroutines

Problem: small kernel size
Solution: small convolutions are pooled into a large matrix-matrix product
Advantage: notionally simple, clearly describes the processing steps in the convolution layers
Disadvantage: naive implementations of matrix products are slow relative current computer progress

Implementation: by using BLAS, an efficient method for computing large matrix-matrix and matrix-vector products
Advantages: a simple and portable way for high-performance linear algebra calculations

• Calling sequences are standardised, programs that call BLAS will work on any computer that has BLAS installed
• High performance on all programs that call BLAS with a fast version of BLAS

Convolution with GPU

Implementation: GPU implementation of CNNs for both training and testing, written as a series of pixel shaders. Each pass (invocation of a pixel shader) leads to one output texture, which is where the result is stored. The previous equations are decomposed into a sequence of GPU passes.

Computation in each pixel shader should be coalesced as much as possible for a succesful performance. First, each pass has a fixed performance overhead in addition to the time needed to perform the actual computations during the pass. Second, eacthe compiler cannot optimise across pixel shaders.

Reduce operations such as summations and matrix-vector products are difficult to perform. The first is achieved over several passes over some fixed number of horizontally adjacent patches. Log(r) N is the number of passes required to sequentially compute the sum. The latter requires a further algorithm to reduce the intermediate result into a vector, requires Log(r) (N+1) passes, with the high performance achieved at r = 10.

All pixel shaders were defined and all textures allocated at the beginning of the program and reused until exit. Only the pixel patch corresponding to the input and the communication were needed for each training sample. This allowed for cost minimisation

Furthermore, conditionals presented a possible burden on performance due to the evaluation of both branches.

If the conditional checked for edge conditions: the conditional should be elided but the input stage of the GPU should be set to "border colour sampling" so that all accesses outside the defined area of a texture would return 0.

If the conditional wasn't on the border: Encoding the condition into a floating point number (greater than 0 iff the condition is true) was the most efficient way.

Advantages (over CPUs):

• Ability to access memory in a 2D manner - row and column access take the same amount of time
• GPUs have several parallel pipelines with independent arithmetic logic units - speeds up computations

Disadvantages:

• Do not have a memory cache
• Do not offer primitive operations for looping and branching