
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article , one will learn about basic idea behind Kullback-Leibler Divergence (KL Divergence), how and where it is used.
| TABLE CONTENTS |
|---|
| Introduction |
| How KL-DIVERGENCE is defined? |
| Why it is not used to measure distance? |
| Illustrations |
| Uses of KL-Divergence |
| KL-Divergence vs Cross Entropy |
| Conclusion |
INTRODUCTION
This article will give a clear insight into Kullback-Leibler Divergence(KL Divergence) . KL-Divergence is something that allows us to measure how far two distributions are apart, this may seem a little bit strange at first, let us see some introduction for it...
Let us assume we have numbers on the real line
For an instance let a=2 and b=5 be the two variables, now to find the distance between the two variables what we usually do is
d(a,b)=|a-b|
If we go one step further and if you are in a coordinate system with x1 and x2 and you have two variables, here for instance as depicted below: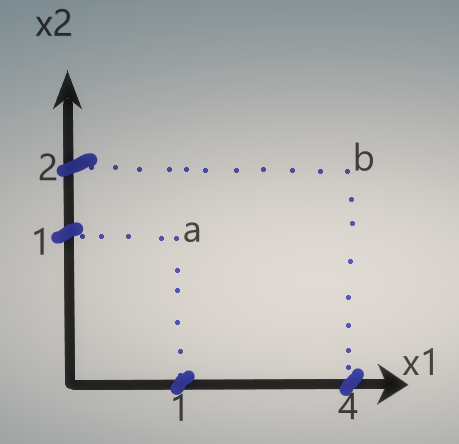 Now to find the distance between a and b :
Now to find the distance between a and b :
d(a,b)=||a-b||
Now let us look at distributions, we look at something that associates the value of X with a potential probability of how likely this value is to occur as follows: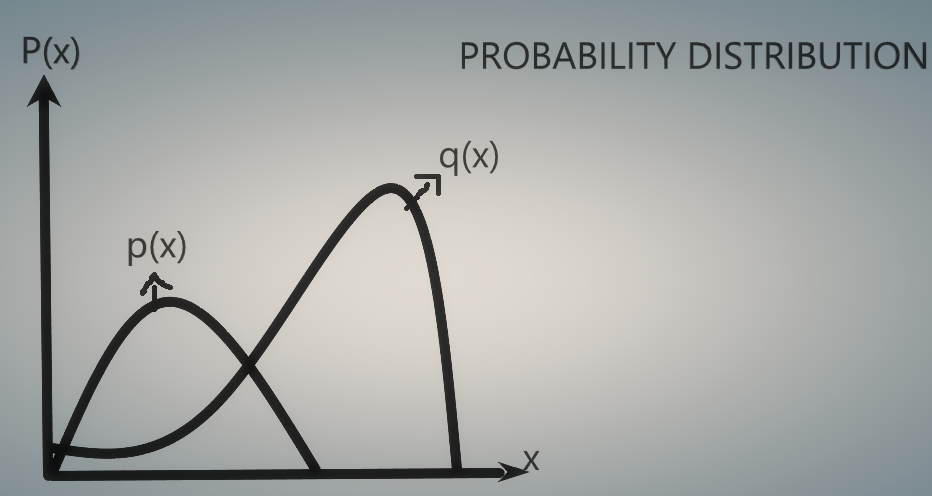 . What is the distance between the two distributions, well that's kind of hard to say, I mean they look different states they have nothing to do with those kinds of points, but the Kullback-Leibler Divergence allows us to find the measure of how far they are apart or how different they are or how different the description of these two is for our random variable. , So this is where the KL-Divergence comes in, let us look more into it.
. What is the distance between the two distributions, well that's kind of hard to say, I mean they look different states they have nothing to do with those kinds of points, but the Kullback-Leibler Divergence allows us to find the measure of how far they are apart or how different they are or how different the description of these two is for our random variable. , So this is where the KL-Divergence comes in, let us look more into it.
How is KL-Divergence defined?
KL-Divergence :
- It is a measure of how one probability distribution is different from the second
- It is also called asrelative entropy.
- It is not the distance between two distribution-often misunderstood
- Divergence is not distance
- Jensen-Shannon divergence calculates the *distance of one probability distribution from another.
- Classically, in Bayesian theory, there is some true distribution
P(X); we'd like to estimate with an approximate distribution
Q(X). In this context, the KL divergence measures the distance from the approximate distribution Q to the true distribution P.
KL-Divergence is defined mathematically as below:

Where the “||” operator indicates “divergence” or Ps divergence from Q.
KL divergence can be calculated as the negative sum of probability of each event in P multiplied by the log of the probability of the event in Q over the probability of the event in P.
The value within the sum is the divergence for a given event.
This is the same as the positive sum of probability of each event in P multiplied by the log of the probability of the event in P over the probability of the event in Q (e.g. the terms in the fraction are flipped). This is the more common implementation used in practice.
Why it is not used to measure distance?
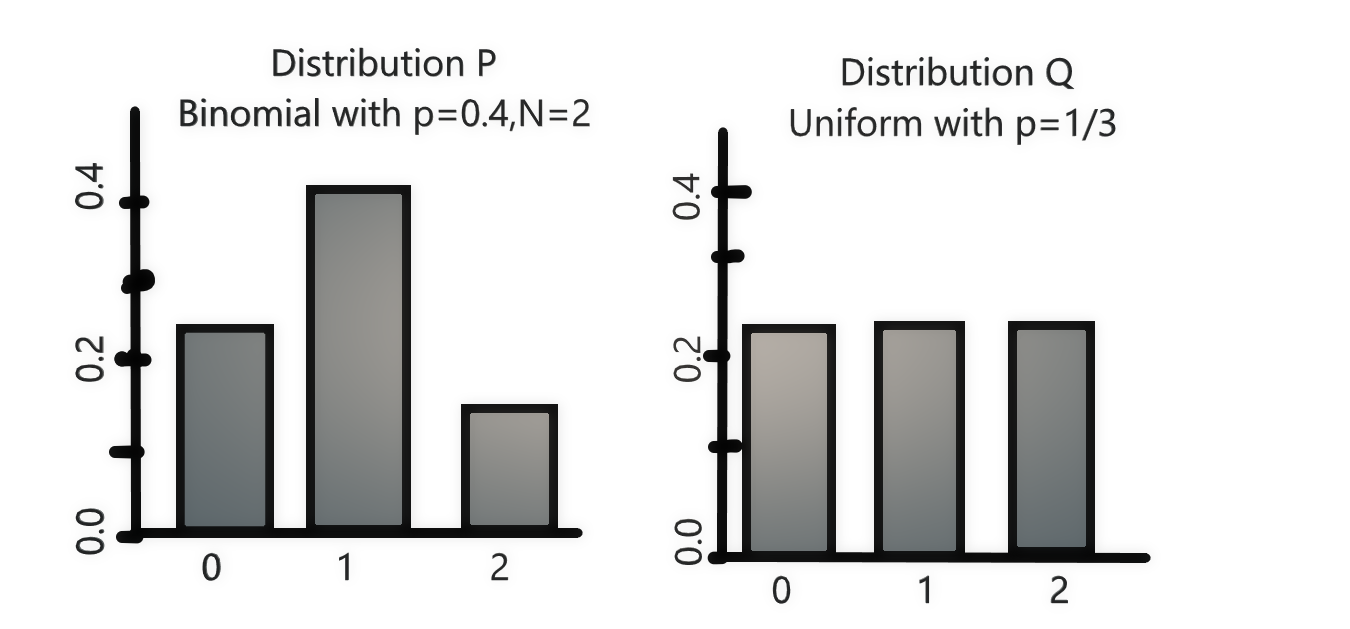
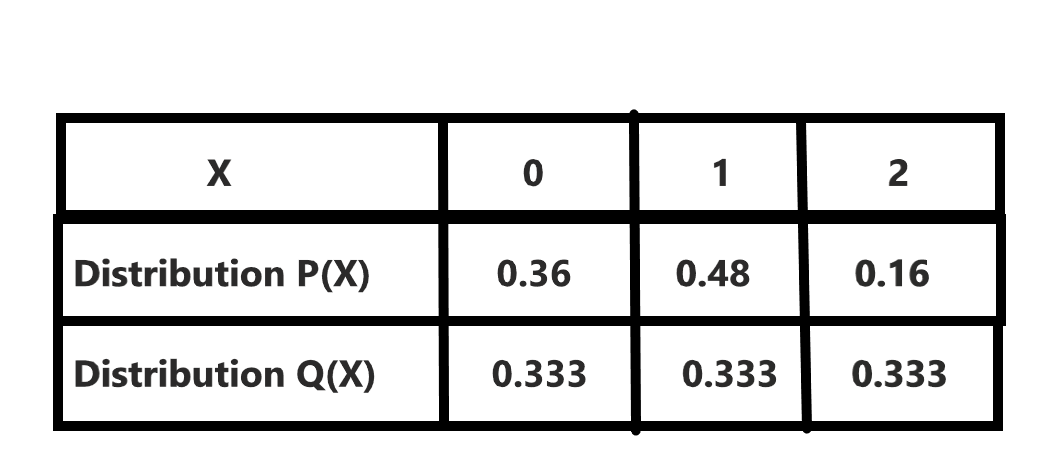
The above is an example consisting of the binomial distribution and uniform probability distribution, The binomial is considered as P and the uniform distribution is considered as Q. One can see for the binomial distribution it has got you may see 3 events 0,1 and 2and having the probability of occurrence of the divine points 0.36,0.48 and 0.16 respectively, the other one is the uniform distribution so the probability is the same 0.333.
So now let us see how can we compute the KL-Divergence for this, the computation is as follows:

as above depicted we simply use the formula which we mentioned before and we simply input the values of P(x) for all three events.
In the above example we have calculated for both P||Q and
Q||P. From the above calculation, we can see that divergence is not symmetric. P to Q is not the same as Q to P.This why we cannot use this method to measure the distance and so it is just used to give the comparison of the probability distribution.
Let us clearly understand the KL-Divergence by some examples
ILLUSTRATIONS
Let us say we are training a neural network to classify dogs and cats in reality which is modeled by some perfect parameters theta (θ) this image will get labeled as 1 0,1 for dog and 0 for the cat. Now let us assume for a minute that our neural network models using parameters Omega (ω) which are our network's weights failed miserably and chose to enable this dog as a cat producing 0.1, that this is a dog and 0.9 that it is a cat, so let's plug these into the formula and then calculate
Pθ(dog)=1 reality Pθ(cat)=0 θ Pω(dog)=0.9 estimate Pω(cat)=0.1 ω
By calculating the values by using the formula as mentioned above we get 3.3
Now let's see what happens if we fix our neural network and now it does a great job instead of 0.1 for the dog we have 0.9 plugging this in we get 0.15 this time which is much lower than the previous 3.3, and it's very close to 0 and in fact, if we had a perfect model KL Divergence would give us precisely 0. Now KL-Divergence is always non-negative. But what's important to realize is that 0 is the minimum and that we get 0 when we have a perfect model as we just said and higher values when we don't as the example discussed before. Let's further more discuss about the KL-Divergence examples:
In python we can use scipy
#example of calculating the KL-Divergence (relative entropy) with *scipy* from scipy.special import rel_entr #rel_entr function is used to compute KL-Divergence
Now let us consider two probability distributions:
#define distributions p = [0.20, 0.40, 0.50] q = [0.60, 0.15, 0.05] # calculate (P || Q) KL_PQ = real_entr (p,q) print('KL(P || Q): %.3f' % sum(KL_PQ)) # calculate (Q || P) KL_QP = rel_entr(q,p) print('KL(Q || P): %.3f' % sum(KL_QP))
The output will be as :
KL(P || Q) = 1.324
KL(Q || P) = 0.397
Why is KL-Divergence useful?? let us discuss below
Uses of KL-Divergence
KL Divergence keeps track of reality by helping the user in identifying the differences in data distributions. Since the data handles are usually large in machine learning applications, KL divergence can be thought of as a diagnostic tool, which helps gain insights on which probability distribution works better and how far a model is from its target.
The intuition for the KL divergence score is that when the probability for an event from P is large, but the probability for the same event in Q is small, there is a large divergence. When the probability from P is small and the probability from Q is large, there is also a large divergence, but not as large as the first case.
It can be used to measure the divergence between discrete and continuous probability distributions, wherein the latter case the integral of the events is calculated instead of the sum of the probabilities of the discrete events.
It is also used to measure the dissimilarity between two probabilities. If we are attempting to approximate an unknown probability distribution, then the target probability distribution from data is P and Q is our approximation of the distribution.
In this case, the KL divergence summarizes the number of additional bits (i.e. calculated with the base-2 logarithm) required to represent an event from the random variable. The better our approximation, the less additional information is required.
The KL divergence is the average number of extra bits needed to encode the data because we used distribution q to encode the data instead of the true distribution p.
Well, we can use KL-Divergence as a loss function or something to optimize strive to get get to a minimum value to zero which is a perfect model the closely related magic cross-entropy s used to accomplish just that ... So how are two related ?? ...
KL-Divergence vs Cross-Entropy vs Jensen–Shannon Divergence
Well, what we can do is we can take the log and split it into subtraction and get the below two terms(marked as pink), and now we can see that the negative part is the cross-entropy.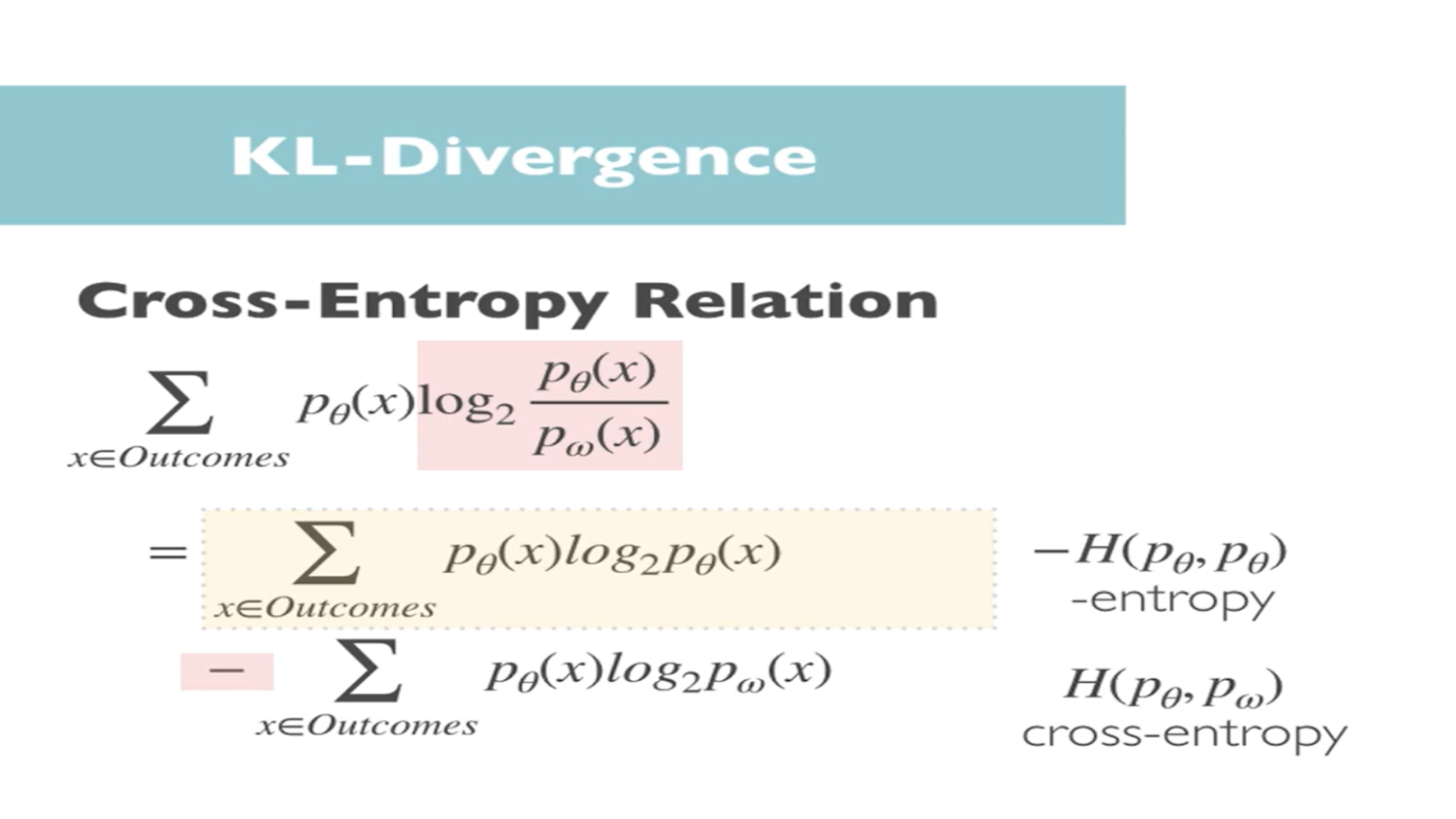
It's simply the definition of the cross-entropy between the two distributions P theta and P omega and then the 1st part is the negative of the entropy of the real distribution with parameters theta notice this is a constant because it's determined by real-world distribution parameters theta which in machine learning would be determined by labels for example, so these don't change and don't depend on our model parameters or network weighs Omega at all, so if we are interested in learning the optimal Omega which only appears in the second term this constant can be ignored, as depicted below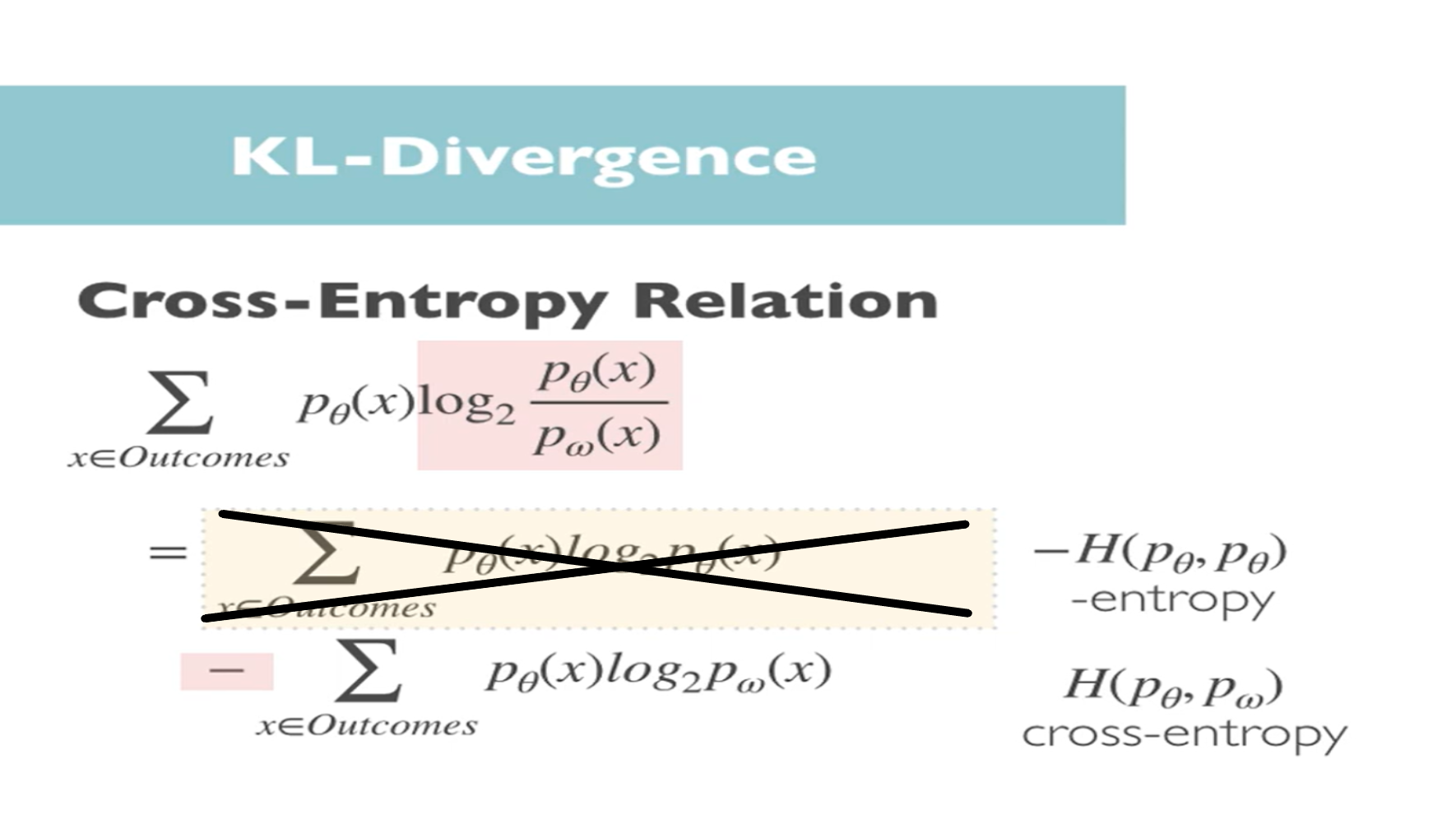
And so we are just left with the cross-entropy so we can see that if we want to minimize the KL-Divergence between the real world distribution with parameters theta and the estimated distribution with parameters omega then this would be equivalent to simply minimizing the cross-entropy between the two.
Now if the optimal Omega would be the same why do we always use cross-entropy when training neural nets, well one reason would avoid the division operation inside the log which is computationally expensive or just overall computing redundant terms like that constant so because the minimization will produce the same Omega we can choose to use cross-entropy but notice that if we are interested in the value of KL-Divergence itself then this would not be the same as cross-entropy.
Now ,
One can see that:
- KL (Kullback–Leibler) Divergence measures how one probability distribution p diverges from a second expected probability distribution q.
- Jensen–Shannon Divergence is another measure of similarity between two probability distribu- tions, bounded by [0, 1]. JS divergence is symmetric and more smooth.
- Jensen-Shannon divergence extends KL divergence to calculate a symmetrical score and distance measure of one probability distribution from another.
Conclusion
In this article at OpenGenus, one must have got to learn a lot about KL-Divergence, especially how the Kullback-Leibler divergence calculates a score that measures the divergence of one probability distribution from another, also one may get to know about the difference between the KL-Divergence and Cross entropy.
Happy learning everyone!!!!!.....
Let's learn and explore together!!!!....
Have a GOOD DAY!!<3......
