Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

In this article, we will learn about the Lempel Ziv Welch compression and decompression algorithm, a famous compression technique that is widely used in Unix systems and GIF format files.

Note that Lempel Ziv Welch algorithm was (USPTO) patented in 1985 by the company Unisys. The patent rights were not enforced but later, royalties were collected. It reduced the popularity of GIF at that time provided an alternative (PNG) was ready.

Table of content:

Introduction to Lempel Ziv Welch algorithm
Advantages of the LZW algorithm
Working of the LZW Algorithm
4. Encoder Algorithm
5. Decoder Algorithm
Important points
Conclusion

Let us get started with Lempel Ziv Welch compression and decompression.

Introduction to Lempel Ziv Welch algorithm

This algorithm was developed by Abraham Lempel, Jacob Ziv, and later published by Terry Welch in the year 1984. Unlike other compression algorithms, the LZW algorithm is a lossless algorithm meaning no data is lost during the compression and decompression of the files.

The algorithm works on the concept that integer codes (numbers) occupy less space in memory compared to the strings literals thus leading to compression of data. The LZW algorithm reads the sequence of characters and then starts grouping them into strings of repetitive patterns and then converts them to 12-bit integer codes which in turn compresses the data without any loss.

Advantages of the LZW algorithm

Advantages of the LZW algorithm are:

The LZW algorithm is faster compared to the other algorithms.
The algorithm is simple, easy, and efficient.
The LZW algorithm compresses the data in a single pass.
The LZW algorithm works more efficiently for files containing lots of repetitive data.
Another important characteristic of the LZW compression technique is that it builds the encoding and decoding table on the go and does not require any prior information about the input.
For some text files, the LZW algorithm tends to have a compression ratio of 60 - 70 %.

Without any do let's jump right into a sample algorithm of the LZW compression technique.

Working of the LZW Algorithm

The Algorithm is broken down into two parts, the encoding algorithm which converts the strings into integer codes, and the decoding algorithm which does vice versa.

Both the encoder and decoder algorithm has a default table or a code-string pair dataset that acts as the initial model for both the encoder and the decoder. And when the algorithm goes on the new integer codes for the various string patterns get added to this table.

Formation of Mapping Table

The mapping table or the string table is predefined with all the default single ASCII characters with codes starting from 0-255. When the input string is sent, it starts with a single character and starts adding characters to it to form newer strings. Each time when it adds a character, it checks if the newly formed string is already in the table else it maps the newly formed string with the next code available in the mapping table, thus creating a new entry in the table.

After updating the table with the new string pattern it again starts with the last added character and starts adding characters to it and again the same process continues. Hence, while we go through the input stream of data, the mapping table gets updated with newer string patterns that are used in the compression.

Encoder Algorithm

As said before, the LZW algorithm creates a translation table that maps the strings to the integer codes and returns the code for the compressed data. And when the algorithm sees the same string again it adds the next character to it and creates a new string. Thus the string gets bigger and bigger which leads to efficient compression of the data.

Steps

Create the Table to map the codes and the strings (here, a dictionary is used)
Create a list to store the codes for the string to be compressed and a variable to store the next code for each string pattern.
Create an empty variable to hold the current string.
For each character in the string (i), append the character to the current variable.
- It checks if the current string is not in the dictionary.
  - Then maps it to the nxt_code and adds it to the dictionary
  - Increases the nxt_code by 1
  - Now, add the code for the current string ignoring the current character i.e. i to the answer list.
  - Now assign the current string to just the current character i.
And before we return the compressed codes, add the code to the current string to the dictionary.
Now, we return the compressed codes for the input string.

def lzw_encoder(string):

    table = dict()
    lis = []

    # creating the table for default compression codes
    for i in range(256):
        table[chr(i)] = i

    current = ''    # a variable to hold the string patterns
    nxt_code = 257  # a variable to hold the next code for the string

    for i in string:
        current += i # appends the current character to the current string
        if ( current not in table ):
            table[current] = nxt_code  # adds a new string pattern to the table
            nxt_code += 1
						current = current[:-1] # deletes the last character of i.
            lis.append( table[current] )
            # appends the code for current string to the answer list

            current = i # reassigns the value of current to i

    lis.append(table[current])
    # adds the last string pattern to the table

    return lis # returns the compressed codes

.
Let's break down how this algorithm works.

This function gets the string to be compressed as the input and then creates a dictionary to store the default codes. This dictionary stores the values for all the possible single characters strings with 0 - 255 codes.

Then, it adds the characters of the input string to the current string variable. It then checks if the current string is in the dictionary if it is in the dictionary it just adds the next input character to the current string variable. When the current string is not in the dictionary it adds it to the dictionary and increases the nxt_code by one.

And after adding the current string to the dictionary, it removes the last character from it and then returns the code for the current string. This is because the current string along with the last character comprises the new string that is added to the dictionary, thus to get the code for the previous string pattern we delete the last character.

And keeps doing this till the entire string is converted into codes. And at last, it adds the code for the remaining string that is stored in the current variable to the dictionary. And then returns the output codes.

Look at the table given below to understand how the encoder works in each step for an example.

Steps	New code in the table	New code in the list
i = 'Y' current = 'Y' Already in the table so moves on	-	[]
i = 'Y' current = 'XY' not in the table, so adds it nxt_code becomes 258 adds code for 'X' after removing 'Y' from current current becomes 'Y'	XY(257)	X(88)
i = 'Y' current = 'YY' not in the table, so adds it nxtcode becomes 259 adds code for 'Y' to the output after removing 'Y' from current current becomes 'Y'	YY(258)	Y(89)
i = 'X' current = 'YX' Not in the table, so adds it nxt_code becomes 260 adds code for 'Y' to the output, after removing 'X' from current current becomes 'X'	YX(259)	Y(89)
i = 'Y' current = 'XY' Already in the table, so moves on	-	-
i = 'Y' current = 'XYY' not in the table, so adds it nxt_code becomes 261 adds code for 'XY' to the output, after removing 'Y' from current current becomes 'Y'	XYY(260)	Y(257)
i = 'Y' current = 'YY' Already in the table, so moves on	-	-
i = 'X' current = 'YYX' not in the table, so adds it nxt_code becomes 262 adds code for 'XY' to the output after removing 'Y' from current current becomes 'X'	YYX( 261)	XY(258)
i = 'Y' current = 'XY' Already in the table, so moves on	-	-
i = 'Y' current = 'XYY' Already in the table, so moves on	-	-
i = 'X' current = 'XYYX' not in the table, so adds it nxtcode becomes 263 adds code for 'XYY' to the output after removing 'X' from current current becomes 'X'	XYYX(262)	XYY(260)
~~ End of the loop ~~ Adds 'X' in current to the output	-	X(88)

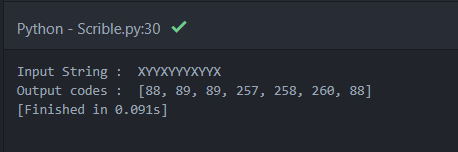
Untitled

Here, is a sample input and output of the LZW encoder algorithm above.

Decoder Algorithm

The decoder does the exact opposite of what the encoder algorithm did. We take the codes given as the input and convert them into the right string patterns and we join them back to get the decompressed string.

Note: Here the dictionary is made of code-string pairs while the dictionary in the encoder is made up of string-code pairs, this is just for flexibility of accessing the required values.

Steps

Create the default table to map all the single characters with the integer codes 0 - 255.
Create a variable to store the previous string and a variable to store the final output string.
Now for each integer code, we add the corresponding string from the table to the answer string.
- If the previous variable has a string in it, the code table gets updated with the new code along with its string.
- The value of the previous variable is set to the string of the current code.
Finally, the output string is returned.

def lzw_Decompress(lis):

    table = dict()

    # Creating a dictionary with default values of codes and strings
    for i in range(256):
        table[i] = chr(i)

    previous = '' 
    nxt_code = 257
    ans = ''

    for i in lis:
        ans += table[i] # adding the strings to the output variable
        if ( previous != '' ):
            table[nxt_code] = previous + table[i][0] # updating the table
            nxt_code += 1

        previous = table[i] # reassigning the previous with the new string 

    return ans

.
Let's understand how the decoder works.

It creates a dictionary of the codes along with the single characters strings just like we did in the encoder. And then it creates the variables to store the output string, the next code to be created, and the previous string.

And then it just adds the corresponding string for each input code to the output variable. If the previous variable contains any string then the if statement gets executed and the table is updated with the new code value.

And when the loop ends the function returns the output string.

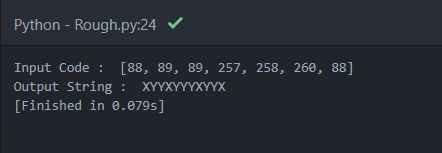
Here is a working example of the LZW decoder, we give the output from the encoder and we get the required string.

out2

Important points

The time complexity and the space complexity of the algorithm is O(n).
The LZW algorithm does not need any prior information about the data to be compressed, thus making it more versatile.
The LZW algorithm adapts to the type of data being processed, thus it does not require any programmer guidance or pre-analysis of data.
The LZW algorithm does not give an optimal compression result always.
The actual compression of the LZW algorithm is hard to predict.

Conclusion

The algorithm given above is not the complete Lempel Ziv Welch algorithm, It is just a mere sample to help you understand how the algorithm works. But it will give you all the required details you need to know about the algorithm.

If you are still curious about it check out the paper published by Welch, Inventor of Lempel Ziv Welch algorithm in 1984 here (PDF on Duke University).

With this article at OpenGenus, you must have the complete idea of Lempel Ziv Welch compression and decompression. Enjoy.

Lempel Ziv Welch compression and decompression

Algorithms List of Mathematical Algorithms