
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 10 minutes
In Lexicographical Permutation Algorithm we will find the immediate next smallest Integer number or sequence permutation. We present two algorithms to solve this problem:
- Brute force in O(N!) time complexity
- Efficient approach in O(N) time complexity
Example : Integer Number :- 329
All possible permutation of integer number : n!
where n is an number of decimal integers in given integer number.
Here, all possible permutation of above integer number are as follows :
1] 239
2] 293
3] 329
4] 392
5] 923
6] 932
The immediate next smallest permutation to given number is 392, hence 392 is an next Lexicographic permutated number of 329
Naive Algorithm O(N!)
-
Step 1 : Find the all possible combination of sequence of decimals using an algorithm like heap's algorithm in O(N!)
-
Step 2 : Sort all of the sequence elements in ascending order in O(N! * log(N!))
-
Step 3: Remove duplicate permutations in O(N)
-
Step 3 : Find the immediate next number of the required number in the list in O(N)
-
Step 4 : stop.
Best Algorithm in O(N)
-
Step 1 : Find the largest index i such that array[i − 1] < array[i].
(If no such i exists, then this is already the last permutation.) -
Step 2 : Find largest index j such that j ≥ i and array[j] > array[i − 1].
-
Step 3 : Swap array[j] and array[i − 1].
-
Step 4 : Reverse the suffix starting at array[i].
Explanation
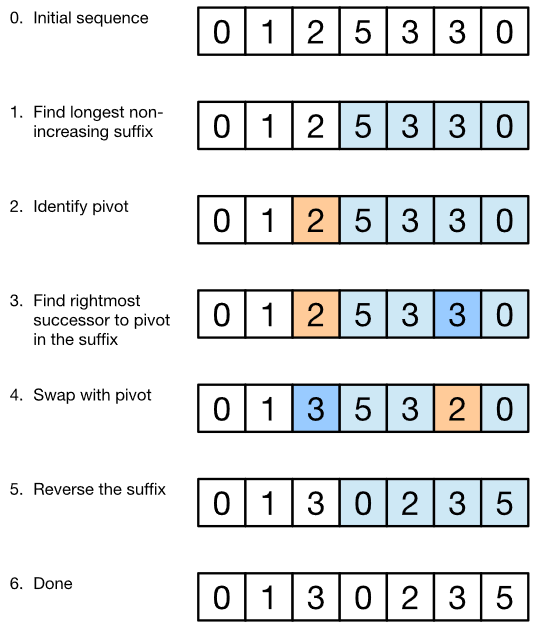
In this algorithm, to compute the next lexicographic number will try to increase the number/sequence as little as possibl and this will be achieved by modifying the rightmost elements leaving the leftmost elements unchanged.
Here above we have given the sequence (0, 1, 2, 5, 3, 3, 0).
Step 1 : Identify the longest suffix that is non-increasing (i.e. weakly decreasing). In our example, the suffix with this property is (5, 3, 3, 0). This suffix is already the highest permutation, so we can’t make a next permutation just by modifying it – we need to modify some element(s) to the left of it. (Note that we can identify this suffix in O(n) time by scanning the sequence from right to left. Also note that such a suffix has at least one element, because a single element substring is trivially non-increasing.)
Step 2 : Look at the element immediately to the left of the suffix (in the example it’s 2) and call it the pivot. (If there is no such element – i.e. the entire sequence is non-increasing – then this is already the last permutation.) The pivot is necessarily less than the head of the suffix (in the example it’s 5). So some element in the suffix is greater than the pivot. If we swap the pivot with the smallest element in the suffix that is greater than the pivot, then the prefix is minimized. (The prefix is everything in the sequence except the suffix.)
Step 3 : In the above example, we end up with the new prefix (0, 1, 3) and new suffix (5, 3, 2, 0). (Note that if the suffix has multiple copies of the new pivot, we should take the rightmost copy – this plays into the next step.)
Step 4 : Finally, we sort the suffix in non-decreasing (i.e. weakly increasing) order because we increased the prefix, so we want to make the new suffix as low as possible. In fact, we can avoid sorting and simply reverse the suffix, because the replaced element respects the weakly decreasing order. Thus we obtain the sequence/number (0, 1, 3, 0, 2, 3, 5), which is the next permutation that we wanted to compute.
Implementation
#include <iostream>
#include <string>
#include <vector>
std::string getNextPermutation(std::vector<int> &v)
{
//find the largest suffix that is non-increasing
int pos_suffix_start;
for (pos_suffix_start = v.size()-1; pos_suffix_start > 0 && v[pos_suffix_start-1] >= v[pos_suffix_start]; pos_suffix_start--);
if (pos_suffix_start == 0)
return "-1";
int pos_pivot = v.size() - 1;
pos_pivot = pos_suffix_start - 1;
// find the rightmost digit in suffix that is the least number greater than the pivot, called as swapper.
int pos_swapper;
for (pos_swapper = v.size()-1; pos_swapper > pos_pivot && v[pos_swapper] <= v[pos_pivot]; pos_swapper--);
//Swap pivot digit with swapper digit
int tmp = v[pos_pivot];
v[pos_pivot] = v[pos_swapper];
v[pos_swapper] = tmp;
//Prepare resulting string with reversing elements after the pivot digit
std::string res = "";
for (int i = 0; i <= pos_pivot; i++)
res+=std::to_string(v[i]);
for (int i = v.size() - 1; i > pos_pivot; i--)
res+=std::to_string(v[i]);
return res;
}
int main ()
{
int number;
std::cout << "\nEnter the Number of digits in sequence : ";
std::cin >> number;
std::vector<int> v;
std::cout << "\nEnter the " << number << " digits : \n";
for (int i=0; i<number; i++)
{
int digit;
std::cin>>digit;
v.push_back(digit);
}
std::cout << "\nThe next lexicograhic number is " << getNextPermutation(v);
}
Complexity
The time and space complexity of Lexicographical (Next)Permutation Algorithm is :
- Worst case time complexity:
Θ(n) - Average case time complexity:
Θ(n) - Best case time complexity:
Θ(n) - Space complexity:
Θ(1)
where N is the number of lines
