
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes
In this article, we have explored the differences between Linear and Logistic regression in depth. We looking into the applications of Linear and Logistic regression along with a basic background.
Linear vs Logistic Regression
Following are the 8 important differences between Linear and Logistic regression:
-
In linear regression, linear relationship is required between dependent and independent variables but no such condition required in logistic regression.
-
In linear regression model, the output is a continuous numerical value whereas in logistic regression, the output is a real value in the range [0,1] but answer is either 0 or 1 type i.e categorical.
-
In linear regression, independent variables can be related to each other but no such scenario should be there in logistic regression.
-
For calculating probabilities, linear regression is not suitable as the output can be negative or greater than 1 too. Logistic regression is quite suitable for such purpose.
-
The linear regression curve is a straight line (or plane/hyperplane). On the other hand, in logistic regression it is "S" shaped.
-
Linear regression is based on least square estimation (for error minimization) while logistic regression is based on maximum likelihood estimation (probability calculation).
-
Talking about computation time, linear regression is faster than logistic regression.
Applications of Logistic and Linear Regression
Applications of Linear Regression
-
The capital asset pricing model (CAPM) uses linear regression. It helps in calculating required rate of return on an asset.
-
Linear regression can be used to study/evaluate market trends and make future predictions.
-
Insurance companies make use of regression to calculate the claims details.
-
We can find out how much dependent variable will change if independent varaible changes. Using this multiple linear regression can be used to find changes in numberical values such as percentage to GPA calculation.
Applications of Logistic Regression
-
Logistic regression is used to predict whether a person can be a probable customer.
-
Can be used to classify people or things based on personel characteristics.
-
In medical field, logistic regression can be used for disease identification, X-rays analysis, MRI analysis etc.
-
Another popular application of logistic regression in weather prediction.
What is Regression
Regression is one of the supervised machine learning algorithm which is used for data analysis and prediction. Supervised learning is the one where data is used to train the model that is already labelled. It means that the correct output or answer is already present. Regression is different from classification such that in regression the output variable is a real or continuous value on the other hand it is categorical in classification.The simplest model of regression is Linear Regression and one of the most popular is Logistic Regression.
Linear Regression
Linear Regression is a regression technique that finds our a relationship between one or more input variables and a single output variable.
In linear regression, the input variable is continuous, unbounded and measured on an interval or ratio scale. If only single input variable is there then it is termed as simple linear regression. If multiple input vairables are there then it is termed as multiple linear regression.
Generalised equation of linear regression looks like this:
y = b0 + b1*x1 + b2*x2 + ... + bn*xn
Here b0,b1...bn are the regression coefficient. These can be found out using techniques such as ordinary least squares, gradient descent, regularization etc.
Simple example of linear regression:
y = b0 + b1*x
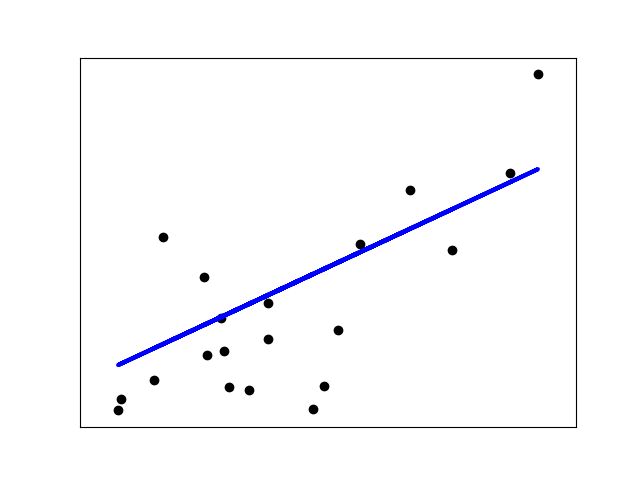
In higher dimensions when we have more than one input (x), the line is called a plane or a hyper-plane.
Logistic Regression
Logistic regression is a regression technique where dependent variable is represented in the binary (0 or 1, true or false) values. This means that the outcome will be in either one of the two forms.
For example, it can be utilized when we need to find the probability of successful or fail event. Here, the same formula is used with the additional sigmoid function, and the value of Y ranges from 0 to 1.
Sigmoid function:
y = 1/(1+e^(-x))
The logistic regression equation can be given as
y = e^(b0 + b1*x) / (1 + e^(b0 + b1*x))
Where y is the predicted output, b0 is the bias or intercept term and b1 is the coefficient for the single input value (x).
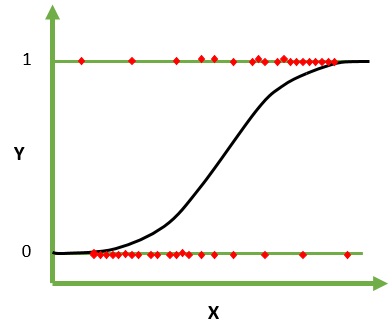
So what we will get as output of the logistic regression algorithm is that it will be in the range of 0<=y<=1. For example if we are trying to predict whether a person is male or female based on human characteristics as parameters, the output can be stated as if y<0.5 the answer is female and if y>=0.5 the answer is male.
The coefficients of the logistic regression are estimated from the training data and is done using maximum likelihood estimation.
With this, you have the complete knowledge of the differences between Linear and Logistic Regression.
