
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 35 minutes | Coding time: 10 minutes
In our previous article, we have discussed implementing the Autocomplete Feature using the TRIE Data Structure. Even though the TRIE Data Structure is an efficient means for implementing large collection of words, they are not regarded as much efficient as implementing all the words in a Dictionary will require 26 Nodes in a standard TRIE. To overcome this problem, Ternary Search Trees were conceptualized and developed where the child nodes of a TRIE Data Structure are optimized as a Binary Search Tree (BST). Ternary Search Trees are seen as a low-memory alternative to the traditional TRIE Data Structure and can store all the words in an English Dictionary at only 3 words per node.
Ternary Search Tree is an optimized TRIE Data Structure (also known as the Prefix Tree or Digital Tree) where the nodes can have a maximum 3 Child Nodes, unlike the TRIE where 26 nodes are optimally associated with a node. Each node in the Ternary Search Tree has three pointers: Left, Middle and Right along with an EndOfWord Bit and a Data Field where the character associated with the string is stored. The Left Pointer is used to point to the node whose value is comparatively lesser than the value in the current node while the Right Pointer is used to point to the point to the node whose value is comparatively greater than the value in the current node. The equal pointers points to the node whose value is equal to the current node value.
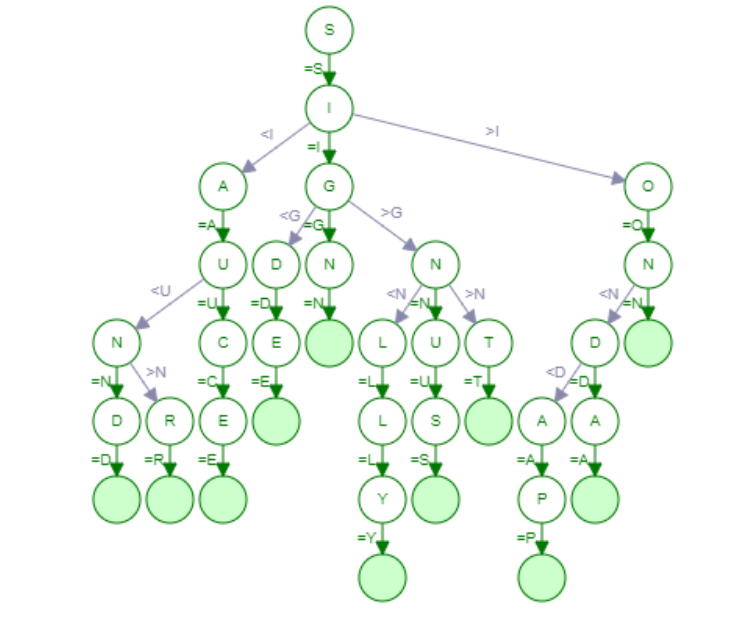
Here is a Ternary Search Tree that has been implemented by entering the following keywords: {'sign', 'sinus', 'sit', 'silly', 'side', 'son', 'soda', 'sauce', 'sand', 'soap', 'sar'}. Ternary Search Trees are quite efficient when it comes to storing the words in a Dictionary and more importantly for the Autocomplete Feature which we are going to implement here. We will use Python-3 Programming Language which is an Open Source, General Purpose and highly extensible Programming Language.
Note that characters in a node are consider if we move beyond that node. In this view, one can imagine the characters to be on the edges instead of the nodes.
Working of Autocomplete Feature in Ternary Search Tree
Autocomplete is now seen as a popular feature across Search Engine, Integrated Development Environments and Text Editors where various possible word predictions are given for a partially written text. The Autocomplete allows for further efficiency while perform queries and typing and here we will use a Ternary Search Tree to implement this feature. Ternary Search Tree is regarded as quite efficient compared to the earlier TRIE Data Structure and can perform insertion, deletion and search operation with the same efficiency as a Binary Search Tree. The Space Complexity associated with a Ternary Search Tree is equal to the length of the string that has been stored into it.
We will input a list of seven words: ["Hell", "Hello", "Help", "Helps", "Hellish", "Helic", "Hellboy"]. Let's input them into our Ternary Search Tree:
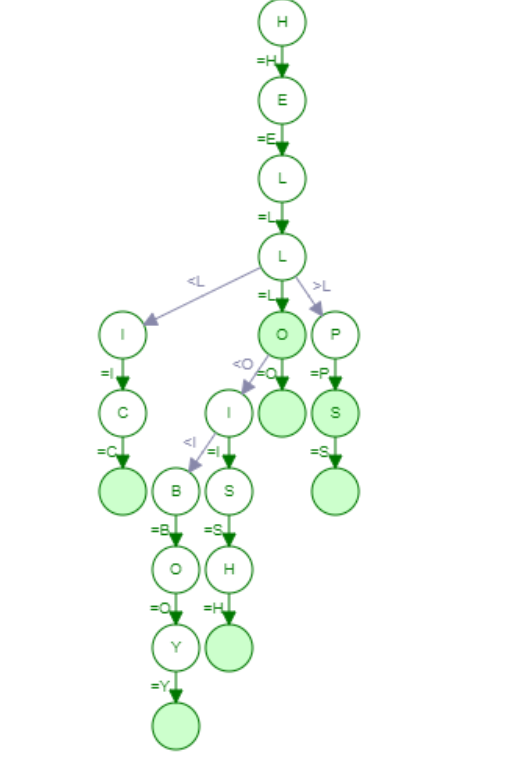
This is the implementation of our Ternary Search Tree. Insertion Operation is relatively easy in Ternary Search Tree and is similar to the one in Binary Search Tree. A character comparison is performed at each stage and the node character is compared to the character to be inserted which gives us three cases:
- If the Character to be inserted is smaller than node value, then move left.
- If the Character to be inserted is larger than node value, then move right.
- If the Character to be inserted is equal to the node value, then move to middle position.
Next we will try to find a word "Help" in our Ternary Search Tree:
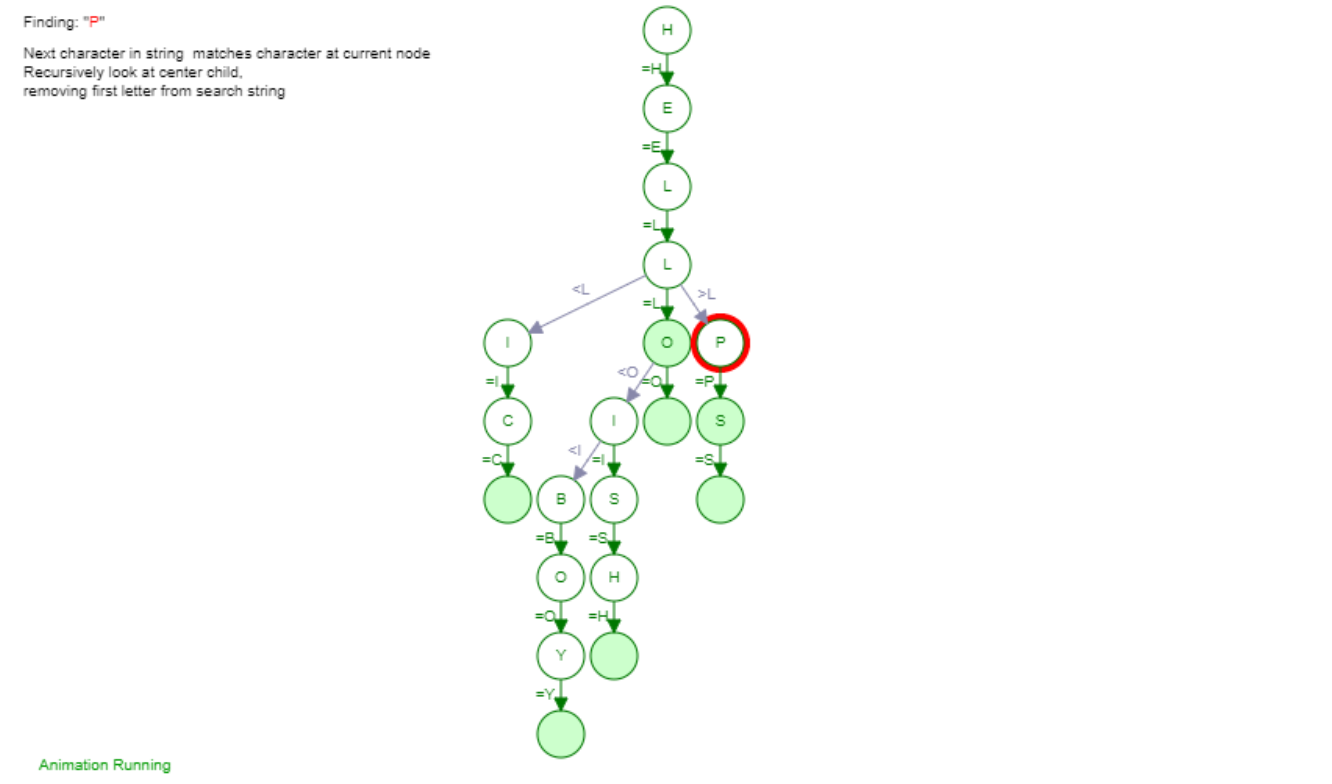
The Search Operation in the Ternary Search Tree is also performed similar to the operation in Binary Search Tree. The next character in the query string is matched to the character present in the current node. The center child is looked upon recursively as the first letter from each string is removed.
"Help" is processed by starting up from the root node and moving ahead as further comparisons are made. The traversal looks like H->E->L->P as the Search Operation terminates when the EndOfString flag variable is marked as 1. When we try to find a string that is not present in the Ternary Search Tree the null node is reached which means that the string is not present in the Ternary Search Tree. If the EndOfString is flagged 1, then the query string is found in the Ternary Search Tree otherwise not.
Once the string has been found, one need to traverse the tree from the current node as the starting point. All words found at this point
The complexity associated with a Ternary Search Tree has been listed below:
1. Average Case Complexity
- Insertion Operation: O(log n)
- Deletion Operation: O(log n)
- Search Operation: O(log n)
2. Worst Case Complexity
- Insertion Operation: O(n)
- Deletion Operation: O(n)
- Search Operation: O(n)
Here is the Pseudocode of performing various operations in a Ternary Search Tree:
1. Insering a Node in the Ternary Search Tree
Go through the pseudocode carefully and you will get the idea:
// Inserting a String in a Ternary Search Tree
function insertNode(node,string){
if(length(string) is equal to 0){
return false;
}
head= first character of string
tail= rest of the characters in the string
if node is None{
node= Take the Head as Node
}
if(head is lesser than character at Node){
// Insert the Character at the Left Branch
node.lo=insertNode(node.lo,string)
}
else if(head is greater than the character at Node){
//Insert the Character at the Right Branch
node.hi=insertNode(node.hi,string)
}
else{
if(length of tail is zero){
node.EndOfString=true;
}
else{
//recursively Pass the rest of the word for insertion
node.eq=insertNode(node.eq,tail);
}
}
return node;
}
2. Searching a Node in the Ternary Search Tree
Go through the pseudocode carefully and you will get the idea:
// Searching a Node in the Ternary Search Tree
function search(node,string){
if node is NULL or length(string) is equal to zero{
return False;
head= first character of string
tail= rest of the characters in the string
if(head is lesser than character at Node){
// Search the Character at the Left Branch
return search(node.lo,string)
}
else if(head is greater than the character at Node){
//Search the Character at the Right Branch
return search(node.hi,string)
}
else{
if length(tail) is zero or endpoint is reached{
return True;
}
return search(node.eq,tail);
}
}
3. Autocomplete in Ternary Search Tree
Go through the pseudocode carefully and you will get the idea:
// Searching a Node in the Ternary Search Tree
function autocomplete(node,string){
if node is none or length(string) is equal to zero{
return False;
head= first character of string
tail= rest of the characters in the string
if(head is lesser than character at Node){
// Search at the Left Branch
return autocomplete(node.lo,string)
}
else if(head is greater than the character at Node){
//Search at the Right Branch
return autocomplete(node.hi,string)
}
else{
if length(tail) is zero{
return all suffixes of node.eq;
}
return autocomplete(node.eq,tail);
}
}
Code Implementation
Following is the complete implementation:
class Node():
def __init__(self, value=None, endOfWord=False):
self.value = value
self.left = None
self.right = None
self.equal = None
self.endOfWord = endOfWord
class Autocomplete():
def __init__(self, word_list):
self.n = Node()
for word in word_list:
self.insert(word, self.n)
def insert(self, word, node):
char = word[0]
if not node.value:
node.value = char
if char < node.value:
if not node.left:
node.left = Node()
self.insert(word, node.left)
elif char > node.value:
if not node.right:
node.right = Node()
self.insert(word, node.right)
else:
if len(word) == 1:
node.endOfWord = True
return
if not node.equal:
node.equal = Node()
self.insert(word[1:], node.equal)
def all_suffixes(self, pattern, node):
if node.endOfWord:
yield "{0}{1}".format(pattern, node.value)
if node.left:
for word in self.all_suffixes(pattern, node.left):
yield word
if node.right:
for word in self.all_suffixes(pattern, node.right):
yield word
if node.equal:
for word in self.all_suffixes(pattern + node.value, node.equal):
yield word
def find(self, pattern):
final_pattern = {pat: set([]) for pat in pattern}
for pat in final_pattern.keys():
word = self.find_(pat)
if word == None:
return None
else:
completions = {x for x in word}
return list(completions)
def find_(self, pattern):
node = self.n
for char in pattern:
while True:
if char > node.value:
node = node.right
elif char < node.value:
node = node.left
else:
node = node.equal
break
if not node:
return None
return self.all_suffixes(pattern, node)
# Driver Function
pattern = ['c']
word_list = ['aardvark',
'altimeter',
'apotactic',
'bagonet',
'boatlip',
'carburant',
'chyliferous',
'consonance',
'cyclospondylic',
'dictyostele',
'echelon',
'estadal',
'flaunty',
'gesneriaceous',
'hygienic',
'infracentral',
'jipijapa',
'lipoceratous',
'melanthaceae']
t = Autocomplete(word_list)
print (t.find(pattern))
##########################################################
The output for the following program would be:
['carburant', 'consonance', 'cyclospondylic', 'chyliferous']
Advantages of Ternary Search Tree
-
Ternary Search Tree is a less memory consuming Data Structure for storing words in a dictionary compared to the traditional TRIE Data Structure.
-
Efficient for near-neighbour lookups and for displaying names with a prefix.
-
Insertion, Deletion and Search Operations in a Ternary Search Tree is quite efficient in terms of Memory and Space.
