Given a string, we are required to find the longest palindromic substring. Ex s="abbbbamsksk". The longest palindromic subtring is abbbba. There are many approaches to solve this problem including DP in (O(n^2)) where n is the length of the string and the complex Manacher's algorithm that solves the problem in linear time. In this article we will be looking into solving the problem using a palindromic tree. We need to learn about how the tree works in order to get the longest palindromic substring.

A palindromic tree is a data structure that has been introduced a few years ago. The tree is a close resemblance to that of a directed graph. The main idea is that a palindrome is a palindrome with a character added before and after it. Ex: babab is a palindrome formed as a result of adding 'b' to aba which, in turn is a palindrome. One thing can be inferred here is for a string of length 'l' there must a palindrome of length l-2 before it and l+2 after it. For example, for ababa, it is aba before it and cababac after it. Now you might think, what about "a", this is still a palindrome. For this, we consider an imaginary string of length -1 (-1+2 = 1).

There are two important edges that can be defined for the tree:

1. Insertion Edge(weighted)
2. Maximum palindromic suffix edge(non-weighted).

Insertion Edge

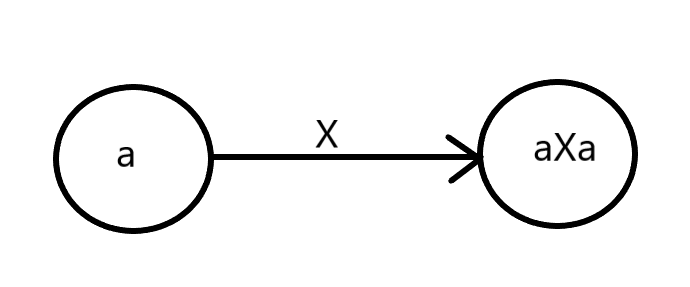
An insertion edge from u to v with a weight of X indicates that v is formed by adding X before and after u.

Maximum palindromic suffix

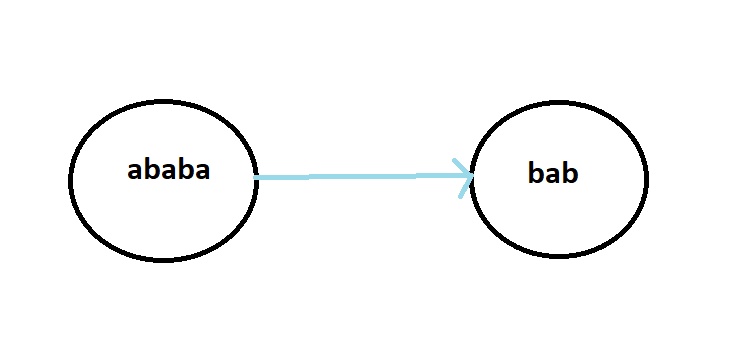
As the title suggests an edge from u to v, suggests that v is the maximum palindromic suffix. Of course u is the maximum palindromic suffix, but, to avoid complexities in form of self loop, we simply omit that.
Note The blue line represents maximum palindromic suffix.

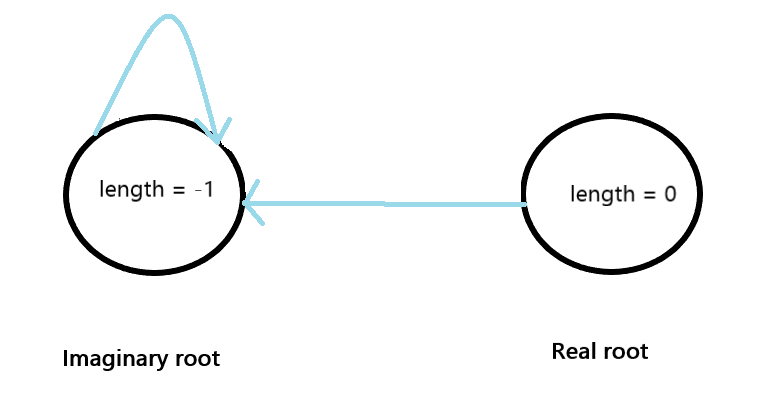
Apart from these two nodes, there are two more which are the root nodes of this entire tree. The first root node has length =-1, as discussed above (a, where length is -1 + 2). We assume that there is an imaginary string of length -1 and add some character, let's say 'a' on both sides, hence we call it the imaginary root. We also have the special case of an empty string where the length is 0, let's call it real root. The longest/ maximum palindromic suffix of the real root is the imaginary root, because it can't be the node itself. And for the imaginary root, the maximum palindromic suffix will be itself (self-loop) as we can't go any higher.

Construction of the palindrome tree

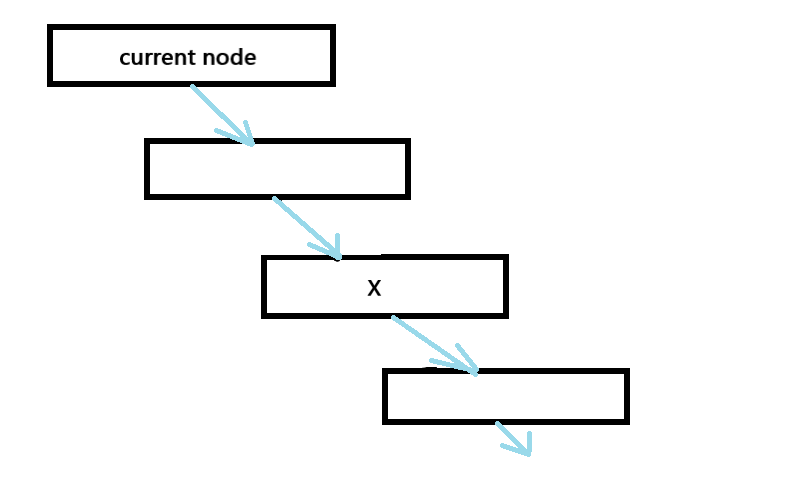
We will process the string one character at a time. At the end of the string, we are left with all the distinct palindromes of the given string.Throughout the program we refer to a node called 'current' which refers to the last inserted node. Let's consider our string S, that has the length n. We have inserted upto k characters starting from 0, now for the next k+1 th character, let's suppose s[k+1] = 'a'. To insert this 'a', we need to find an X such that aXa is a palindrome. Also, note that our current node holds the longest palindrome up to the index k. This node in turn holds other nodes which are the longest palindromix suffix. The search for X starts with current node itself, if it is the suffix we are looking for, then good, else we traverse down till we find the X, such that aXa is a palindrome.

Look at the below image for better understanding.

Example

Consider string S="abb".

1. Start with S[0] = 'a', as mentioned before our tree has two roots. Insertion always starts with the current node, in our case is the imaginary root. Inserting 'a' on an imaginary root with length -1 will yield us a string of length 1. Hence we have an insertion edge from imaginary root to the new node 'a', whose suffix will link to the the empty string, i.e real root.
   
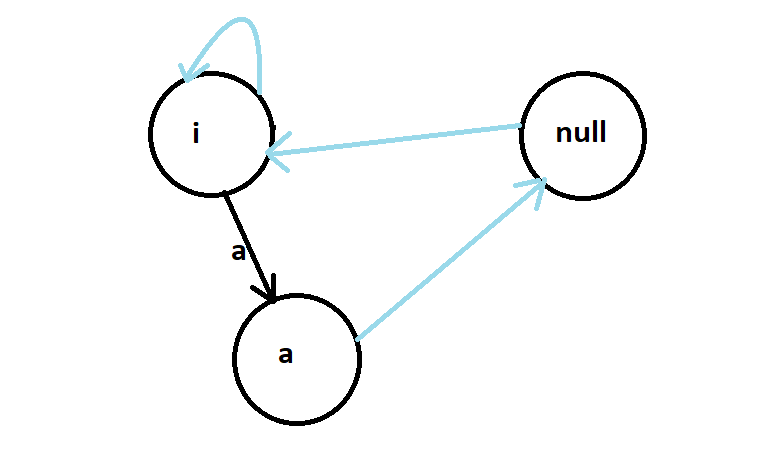
2. Now for S[1] = 'b', we start with the current node which is 'a', we will traverse the suffix chain till we find X, such that bXb is a palindrome, this brings us back to the imaginary root. And as in the previous one, the suffix of the 'b' is the real root.
   
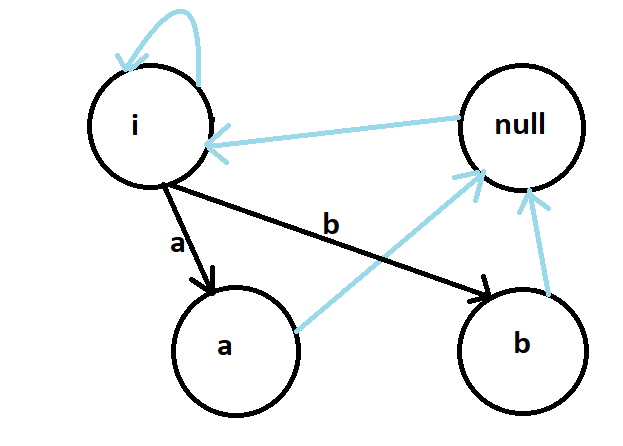
3. Now for the final character S[2]='b', we start from the current node, we will traverse till we find X, in this case X is an empty string, i.e we will stop at the real root. Adding 'b' to an empty string on both sides gives us "bb" which is the longest palindromic substring.
   

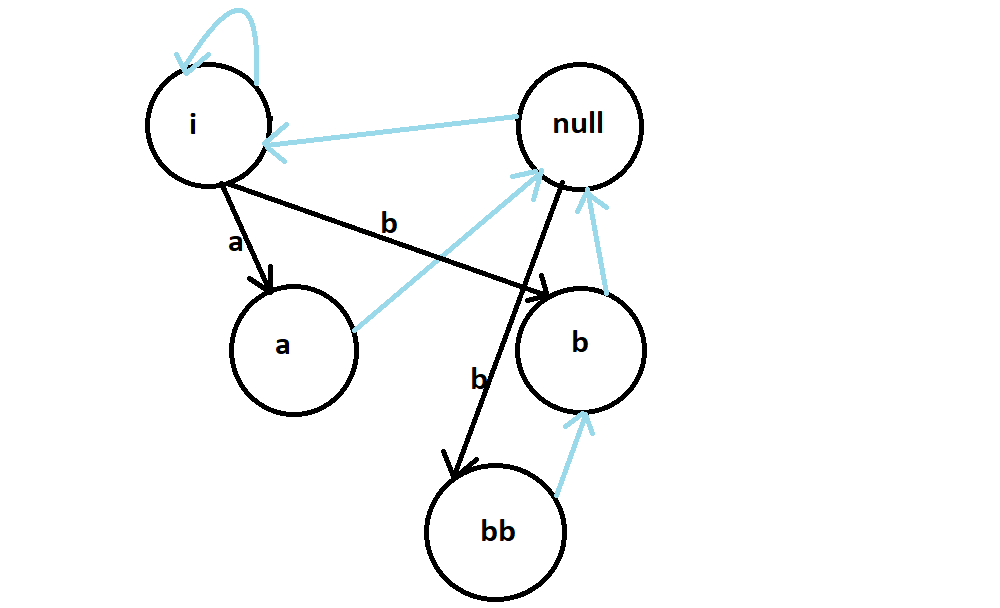
Implementation

Storing all the palindromes will be really inefficient in terms of memory. The question is do we really have to have the strings stored. The answer is No. We are simply creating a structure that would hold the required information. This structure has start, end that holds the start and end indexes of the current node inclusively. The length stores the length of the substring. We are maintaining an array of integers to store insertion edges whose size is 26 (from a to z). Every time we are creating a new node, the insertionEdge of the weight of the vertex will be updated to ptr which stores the node value to which the edge is pointed to. In addition we are having a suffix edge variable which is called max_suffix, a current_node that has the last inserted character. The ptr value for root1 (imaginary root) is 1 and for root 2(real root) is 2. Both the roots are of type structure and their values are initialized at the beginning of the program. We also have a tree[] which is an array of structure to store the entire data required for the construction of the palindromic tree.
Now to the insert(), this function is called in the main() in a loop inserting every single character of the input string.
This function can be divided into two parts:

1. find X
2. checking if s[current_index] + X + s[current_index] already exists.

As explained above, we always start with the current node, and check if adding s[current_index] will make it a palindrome or no. For this we simply have to compare the fo\irst character of the current node to s[current_index]. If they are the same, then we found our X, else we have to go to the current node's suffix edge and repeat the same process.

 int temp = current_node;
 while(true){
 int current_length = tree[temp].length;
   if(current_index - current_length >=1 && (s[current_index -1] == s[current_index -                          current_length - 1])) 
    break;
   temp = tree[temp].max_suffix;
 }

Now, we check if s[current_index]+X+s[current_index] already exists, we can do so by checking if the temp (which is X) has an insertion edge with the label s[current_index]. If so, we update the current node, else we create a new node.

if (tree[temp].insertionEdge[s[current_index] -'a'] != 0) 
    { 
        current+node = tree[temp].insertionEdge[s[current_index] - 'a'];   
        return; 
    }

For the new node, the ptr will be incremented and all the variables in the structure will be filled accordingly. For the maximum suffix of a node, the ptr value of the suffix will be stored in max_suffix. For ex, if the string is of length 1, then it's max_suffix will be 2, ptr=2 is basically the real root. For finding max_suffix we repeat the same process of finding X.

Let's see the code implementation:

#include<bits/stdc++.h>
#define MAXN 1000
using namespace std;

struct node{
int start, end;
int length;
int insertionEdge[26];
int max_suffix;
};

node root1, root2;
node tree[MAXN];

int current_node;
string s;
int ptr;

void insert(int current_index){
 
 int temp = current_node;
 while(true){
 int current_length = tree[temp].length;
   if(current_index - current_length >=1 && (s[current_index -1] == s[current_index -                          current_length - 1])) 
    break;
   temp = tree[temp].max_suffix;
 }
 
 if (tree[temp].insertionEdge[s[current_index] -'a'] != 0) 
    { 
        current+node = tree[temp].insertionEdge[s[current_index] - 'a'];   
        return; 
    }
  ptr++; 
  
    tree[temp].insertionEdge[s[current_index] - 'a'] = ptr;   
    tree[ptr].end = current_index;   
    tree[ptr].length = tree[temp].length + 2;   
    tree[ptr].start = tree[ptr].end - tree[ptr].length + 1; 
    
    current_node = ptr; 
    temp = tree[temp].max_suffix; 
    
     if (tree[current_node].length == 1) { 
        tree[current_node].max_suffix = 2; 
        return; 
    } 
    
    while (true) { 
        int current_length = tree[temp].length; 
  
        if (current_index - current_length >= 1 && (s[current_index] == 
             s[current_index - current_length - 1])) 
                break; 
  
        temp = tree[temp].max_suffix; 
    } 
  
    tree[current_node].max_suffix = 
        tree[temp].insertionEdge[s[current_index] - 'a']; 
 }
 
 int main(){
 root1.length = -1;
 root1.max_suffix = 1;
 
 root2.length = 0;
 root2.max_suffix = 1;
 
 tree[1]=root1;
 tree[2]=root2;
 
 ptr=2;
 current_node=1;
 s = "abb";
 for(int i=0; i<s.size(); i++)
     insert(i);
     
 int last=ptr;
 
 for (int i = tree[last].start; i <= tree[last].end; i++) 
                cout << s[i]; 
  
 return 0;
 
 }

Output

bb

Time Complexity

O(n) where n is the size of the string. You might have a doubt regarding the process of finding X. Does that increase the complexity? The number of iterations to find the value of X is roughly constant when compared to the size of the string. Hence we can ignore it.

Comparision with other approaches

As mentioned in the beginning, there are a number of approaches that vary not only in the time complexity but also in the core logic and subsequently the implementation.

1. We have used a palindromic tree here, we could also go with a brute force approach that would find every substring and then check for it to satisfy the palindrome condition. The time complexity for this is O(n^3) and space complexity is O(1).
2. We can solve this using Dynamic Programming as well, here we completely omit the checking for palindrome procedure. We start in a bottom up fashion, maintain a boolean table for every substring. The time complexity is O(n^2) and space complexity is O(n^2).
3. This problem can be solved in linear time with Manacher's algorithm. In this algorithm we can find a palindrome by starting from the center of the string and comparing characters in both directions one by one. If corresponding characters on both sides match, then they will make a palindrome.

Now that we've at least got a gist of other approaches, we can find the obvious differences in time complexities and the core logic. Except for the DP approach the other methods didn't use any extra space. Palindromic tree can be handy to solve other problems other than the current one which include finding the number of occurrences of each subpalindrome in the string and also the number of palindrome substrings. Even the DP table can be used to find the number of palindromic substrings. But, the rest approaches, they have one sole purpose which is to find the longest palindromic substring, this includes the Manacher's too.

Applications

Other than finding longest palindromic substring the palindromic tree can also find

1)The number of occurrences of each subpalindrome in the string
2)The number of palindrome substrings etc.

With this article at OpenGenus, you must have a complete idea of Palindromic Tree and how it can be used to solve the longest Palindromic substring problem. Enjoy.

Learn more:

• Longest Palindromic Substring using Dynamic Programming by K. Sai Drishya
• Manacher's Algorithm by Piyush Mittal
• Palindromic Tree (Eertree) by Yash Aggarwal
• Find minimum number of deletions to make a string palindrome by Abhiram Reddy Duggempudi
• List of Dynamic Programming problems at OpenGenus
• List of Data Structures at OpenGenus