Reading time: 40 minutes | Coding time: 10 minutes

We are given two numbers M and N. Our aim is to find the highest power of N that divides Factorial of M (M!). We often come across such problems in competitive programming where we require an optimal solution.

First we will discuss about the Brute Force approach and then we will be discussing this problem using Legendre’s formula.

Underlying are some examples which would help in better understanding of the problem.

EXAMPLES

Input : M = 5, N = 2
Output : 3
Explanation: Value of 5! is 120. The largest power
of 2 that divides 120 is 8 (or 2³)

Input : M = 146, N = 15
Output : 35
Explanation: 15³⁵ divides 146! and 35 is the largest such power of 15.

Input: M = 7, N = 3
Output: 2
Explanation: 3² divides 7! and 2 is the largest such power of 3.

Input: M = 10, N = 3
Output: 4
Explanation: 3⁴ divides 10! and 4 is the largest such power of 3.

Input : M = 100, N = 2
Output : 97
Explanation: 2⁹⁷ divides 100! and 97 is the largest such power of 2.

Input : M = 100, N = 3
Output : 48
Explanation: 3⁴⁸ divides 100! and 48 is the largest such power of 3.

BRUTE FORCE APPROACH

The most basic approach to this problem is by going step by step into the subparts lying below.

Algorithm

1.Compute factorial of given number M : facto=M!
2.Declare an array for storing all the powers which will be dividing M!
3.Initialising variable: power = pow(N,i) where i = 1;
4.while ( power <= facto)
5.if ( facto % power == 0)
6.arr[j] = i;
7. Increament i
8. Calculate power: power = pow(N,i)
9.Find greatest element in array arr a for the result.

IMPLEMENTATION(C++)

// Part of OpenGenus IQ
#include<bits/stdc++.h>
#include <iostream>
using namespace std;
int main()
{
    int fact,n;
    cin>>fact>>n; // taking input from user (factorial and the number)
    long long int facto=1;
    for(int i=2 ; i<=fact ; i++)
    {
        facto = facto * i;
    }
    int arr[50]; // array for storing all the powers which will divide the  factorial of given number 

    int i=1,j=0; // i for counting powers and j for indexing array
    long long int power= pow(n,i);
    while(power <= facto)
    {
        if(facto % power == 0)
        {
            arr[j] = i;
            j++;
        }
        i++;
        power = pow(n,i);
    }
    int maxim=INT_MIN;
    for(int i = 0 ; i < j ; i++)
    {
        if(arr[i] > maxim)
        {
            maxim = arr[i];
        }
    }
    cout<<"The highest power of a n that divides (fact !) is " << maxim;
}

TIME COMPLEXITY OF BRUTE FORCE APPROACH

Break down of the Complexity:

1. We calculated the factorial of number'fact' which has a linear complexity O(fact) because factorial's complexity is directly proportional to the number fact.
2. While loop which is dependent on the complexity of power function which has a complexity O(log i).i here depicts the power of the number which is to be caluclated and this power in while loop is being called here i number of times. The total complexity of this loop is ~i(log i).
3. And lastly a loop with complexity O(j) for calculating maximum .This will be negligible.

The complexity of this code is complex .

O(fact) + i * O(logi)

CHALLENGES WITH BRUTE FORCE APPROACH

Though the basic approach seems simple but the problem with this approach is that the simple factorial function is capable of calculating factorial upto 20 even after using long long datatype. Even if we use the approach for calculating Large number Factorial, the complexity of this code would remain high . Here in the while loop we are checking power from 1 and upto M! and furthur storing the power which satisfies condition in different memory location. This makes the complexity of code higher for Large numbers. Thus. this approach can be used for small M. Therefore we now go to optimal approach of this problem.

Legendre’s formula Approach

Given an integer M and a prime number p, find the largest x(power) such that pˣ (x raised to power p) divides M! (factorial).

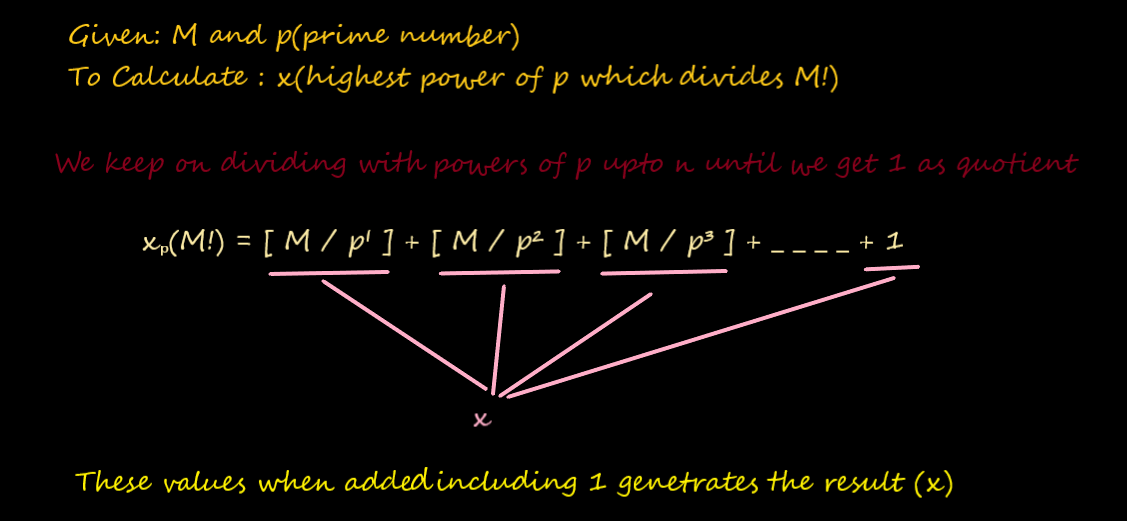
Here , the given Number M is divided by p¹,p²,p³ .... until we get 1 after division. Then all the consecutive quotient are added including 1 which gives the highest power of p which divides M factorial .(M!).

How many numbers in {1, 2, 3, 4, ….. M} are divisible by p?
Every pᵗʰ number is divisible by p in {1, 2, 3, 4, ….. n}. Therefore in M!, there are n/p numbers divisible by p. So we know that the value of x (largest power of p that divides M!) is at-least n/p.

Example

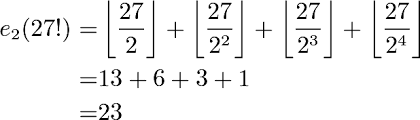
Explanation
In this example for computing the highest power 2 that divides 27! 27 is divided by 2 resulting in 13 , then it is divides by 4 resulting in 6 , then it is divides by 8 resulting in 3 , then it is divides by 16 resulting in 1. When we reach 1 we furthur stop diving the number . And on adding all these numbers 13+6+3+1 = 23 .
Thus 23 is highest power of 2 that divides (27!).

IMPLEMENTATION OF LEGENDRE'S FORMULA(C++)

// Part of OpenGenus IQ
// C++ program to find largest x such that p*x divides n!  
#include <iostream> 
using namespace std;  

// Returns largest power of p that divides n!  
int largestPower(int n, int p)  
{  
    // Initialize result  
    int x = 0;  

    // Calculate x = n/p + n/(p^2) + n/(p^3) + ....  
    while (n)  
    {  
        n /= p;  
        x += n;  
    }  
    return x;  
}  


int main()  
{  
    cout<<"ENTER THE NUMBER AND PRIME NUMBER";
    int n,p;
    cin>>n>>p;
    cout << "The largest power of "<< p << 
            " that divides " << n << "! is "<<  
            largestPower(n, p) << endl;  
    return 0;  
}

COMPLEXITY

Time complexity of the above solution is Logₚn.

EXPLANATION

In this code , the function is passed with values n and p and in that function ,p is divided by n again and again until we get 1 and simultaneously the quotient we get after diving p by n each time is added to x . Thus the result x has the highest power.

(27!) = [27/2] = 13 , then we divide [13/2] = 6 , then we divide [6/2] = 3 , then we divide [3/2] = 1 , thus by adding 13+6+3+1 =23 , which is the result.

Legendre’s formula Approach (where N can be any NUMBER)

FINAL SOLUTION

While dealing with this problem to find the maximum power of N that divides M factorial (M!), N can be anything prime or composite. Thus in this case,

• calculate the prime Factors of the given number N .
  • Prime factor is the factor of the given number which is a prime number.
    In simple words, prime factor is finding which prime numbers multiply
    together to make the original number. Example: The prime factors of 15 are 3
    and 5 (because 3×5=15, and 3 and 5 are prime numbers).
• Calculate highest power for all prime Factors (N1,N2,_ _ _)
• The prime Factor with lowest value of the highest power of N that divides M!
  is the result.

EXAMPLE

fact = 146, n=15
First find the prime factor of 15 that are 3 and 5 then first divide with 3 and add i.e.

Applying Legendre’s formula for prime factor 3.

[146/3]+[48/3]+[16/3]+[5/3]+[1/3] = 70
   48  +   16  +  5  +  1  +  0   = 70

There is 70 is maximum power of 3 prime number.
146! is divisible by 3^70 which is maximum.

Applying Legendre’s formula for prime factor 5.

[146/5]+[29/5]+[5/5]+[1/5] = 35
   29  +   5  +  1  +  0   = 35

There is 35 is maximum power of 5 prime number.

Result

Finally we return minimum of all found powers.
Minimum of two powers is 35 which is our answer.

IMPLEMENTATION (C++) (USING LEGENDRE'S FORMULA)

// Part of OpenGenus IQ
#include <bits/stdc++.h> 
using namespace std; 

//Application of legendre's FORMULA
int findPowerPrime(int fact, int p) 
{ 
    int res = 0; 
    while (fact > 0) {         
        res += fact / p; 
        fact /= p; 
    } 

    return res; 
} 

// Returns sum of all factors of n. 

int findPowerComposite(int fact, int n) 
{ 
    // To store result (minimum power of a prime factor that divides fact! )  

    int res = INT_MAX; 

    // Traverse through all prime factors of n.

    for (int i = 2; i <= sqrt(n); i++) {         

        // counter for counting the power of prime number

        int count = 0; 
        if (n % i == 0) { 
            count++; 
            n = n / i; 
        } 

        if (count > 0) { 

            // Maximum power of i that divides  fact!. We divide by count to handle multiple occurrences of a prime factor.

            int curr_pow = findPowerPrime(fact, i) / count; 
            res = min(res, curr_pow); 
         } 
    } 

    // This condition is to handle the case when n is a prime number greater than 2. 

    if (n >= 2) { 
        int curr_pow  = findPowerPrime(fact, n); 
        res = min(res, curr_pow); 
    } 

    return res; 
} 


int main() 
{ 
    int fact , n; 
    cin>>fact>>n;
    cout << findPowerComposite(fact, n); 
    return 0; 
}

COMPLEXITY

Time complexity of the above solution is Logₙ(fact).Here we add an additional
loop which is used to find the prime factors of number n . But we cannot
direct;y multiply the complexity by sqrt(n) because the calling of
findPowerPrime is not directly dependent on sqrt(n) or n , because n is changing
everytime with n=n/i and that too not everytime and everytime n changes the
value of sqrt(n) also changes so we cannot directly determine the multiplying
complexity with Logₙ(fact).

EXPLANATION

The programs Execution starts as the call to the function findpowerCompostite(fact,n). In that function , We traverse through all the prime factors a number can have . In the loop inside this function we traverse upto sqrt(N) to find the prime factor of the number because

If a number n is not prime, it can be factored into two factors a and b:
n = a * b
If both a and b were greater than the square root of n, then a * b would be greater than n. So at least one of those factors must be less than or equal to the square root of n, and if we can't find any factors less than or equal to the square root, n must be prime.

So after calculating prime factor we go on to pass fact and the prime factor(i) to calculate power using Legendre's Formula .The function find power prime calculates highest power of fact with prime no i using legendres's formula . If on dividing N by i (N=N/i) if we get a N which is greater than 2 then we again pass into the function find power prime to get the highest power of N that divides fact(fact!) . We simulatneously keep on finding the minimum value of the res that is returned by find power prime and thus in the end we get the Minimum result .

QUESTIONS

With this article at OpenGenus, you must have the complete idea of the algorithm to find the maximum power of N that divides M factorial (M!). Enjoy.