Number of unique partitions of an integer

Reading time: 40 minutes

Examples

Input: 3
Output:
3
2 1
1 1 1
Here (2,1) and (1,2) are permutations of each other thus only one of them is mentioned as we need to generate unique partitons. 
Input: 4
Output:
4
3 1
2 2
2 1 1
1 1 1 1
Here (3,1),(1,3) and (2,1,1),(1,2,1),(1,1,2) are permutations of each other and thus only one of them is generated.

Here we will be using two methods to solve the above problem:

• the first is the naive approach which uses brute force method to generate all possible compositions and separate the unique compositions. This takes O((N^N)log N) time complexity

• Another approach will be to use dynamic programming to generate all the compositions in decreasing order. This approach is much more optimal then the naive approach as it generates only unique partitions. This takes O(2^N)

Naive Approach

The Naive approach uses brute-force method to generate all the possible compositions possible by partitioning the given number. We maintain a hash map here to check whether the currently generated composition is already included or not. If already included no need to update the ans else update the ans and include the entry into the hash map. But to check whether a composition is already present in the map or not we need to define an encoding scheme to convert the partition array of integers into a sorted string of characters which can be hashed with their corresponding integer counts. Sorting is required as (1,2) and (2,1) should be considered same.

p[] = { 1, 2, 4 } encoded to s[] = "1|2|4"
p[] = { 2, 20, 3 } encoded to s[] = "2|3|20"
p[] = { 5, 1, 1 } encoded to s[] = "1|1|5"

The hash map created will be of the form-

map< string, bool >Hash_Map;
Here for every unique string partition generated boolian value will be 1 else 0.

Pseudo Code

Number_of_unique_partitions( n, p[], Hash_Map )
[ n is the input number, p[] is the integer partition array, Hash_Map is the mapping of unqiue partitions]
1. If n=0 or n=1 then no more partitioning possible thus encode the current partition array of integers into a sorted string of characters each separated by a  separator '|' and follow step 2.
2. If the corresponding string is already mapped then no need to update the ans otherwise update the answer and print the corresponding partition array p[].
3. If n is greater than 1 we call recursively by partitoning n into smaller components and updating the partition array respectively.  

Complexity of naive approach

• Time complexity: O((n^n)logn)
• Space complexity: O(2^n)

As there are n^n recursive calls and each composition needs to be sorted in nlogn and encoding can be done in another n time units. Thus the complexity of the above approach will be O((n^n)logn). The space required to built the hash map will be of the order O(2^n) as 2^n compositions are possible.

Dynamic Approach

Here we can see that in the 2nd example (2,1,1) composition can be obtained by partitioning the rightmost 2 into 1 + 1 from the composition (2,2). Thus we only need rightmost 2 to search for other compositions which forms the base of our dynamic approach as we do not need to evaluate the partition array from the beginning every time.

The idea is to move recursively from n which is the maximum possible value for the partition to 1 which is the minimum possible and keep on appending the numbers used to form the required sum in the array. When the sum becomes equal to n then we print the array and return after increasing the counter variable. This forms the base case of our recursive logic.

Then we have started forming required sum using the maximum value number used in the previous partition. If that number becomes greater than n we ignore it else we append that number to the array and move recursively to next iteration to form

new_rem_val = rem_val – i  as i is appended 
and where max value number( max_val ) that could be used is less than or equal to i.

This way we can generate the all the required unique partitions from a given number. The complexity of the above approach will be O(c) as there are c unique partitions and we need to generate all the c partitions. Here c can take a maximum value of 2^n as there are a total of 2^n possible partitions. Thus this approach will have a worst case time complexity of O(2^n).

Let us consider the example for n=10. The partitions generated via the above discussed dynamic approach will be as follows:

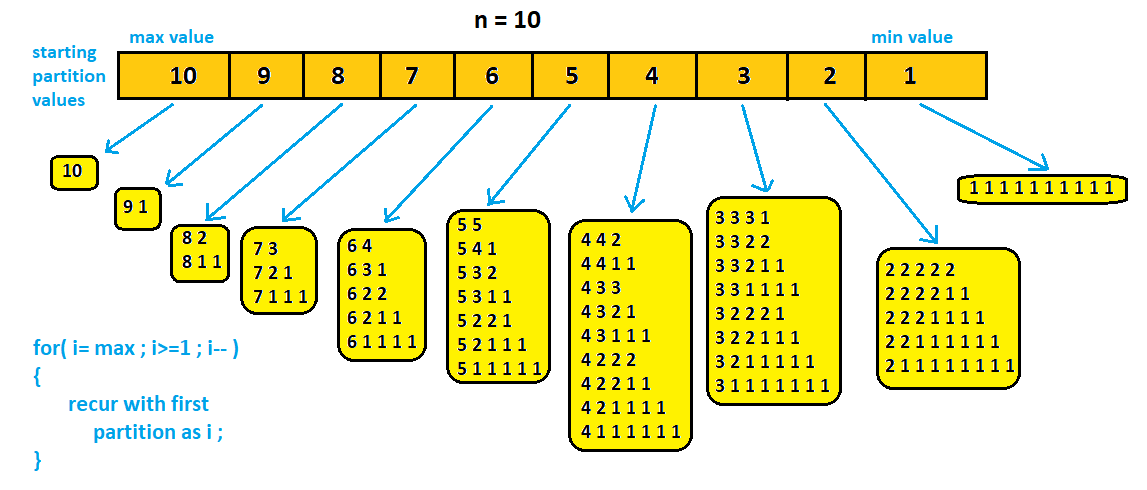
following is the implementation of the above approach:

Source Code

// C++ program to generate the number of unique partitions of a number
#include <bits/stdc++.h>
#define mx 100000
#define ll long long
#define f(i,a,b) for(i=a;i<b;i++)

using namespace std;

// dp array to store the partition values, also known as partition array
// c is the counting variable to count unique partitions
ll int dp[mx], c=0;

// Function to generate the unique partition array for positive integer n and print it
// rem_val is the remaining value still need to be formed
// max_val is the maximum number that can be used in the formation of rem_val
void find_unique_partitions(ll int idx, ll int rem_val, ll int max_val)
{
    ll int i=0;
    if (rem_val== 0)
    {
        f(i,1,idx)
            cout<<dp[i]<<" ";
        cout<<endl;
        c++;
    }
    else {
        for(i=max_val; i>=1; i--)// since a partition value "i" cannot exceed max_val and cant be less than 1.
        {
            if (i>rem_val)
                continue;
            else{
                dp[idx] = i; // allocate i to the current index
                find_unique_partitions( idx+1, rem_val-i, i); // now max_val is updated to be i
            }
        }
    }
    return ;
}

int main()
{
    //t is number of test cases
    //n is the given integer for each test case
    ll int t,n;
    cout<<"Enter the number of test cases: ";
    cin>>t;
    while(t--)
    {
        cout<<"Enter the number( positive integer): ";
        cin>>n;
        c=0;
        cout<<"Following are the unique partitions: "<<endl;
        find_unique_partitions(1, n, n);
        cout<<"Total no. of unique partitions: "<<c<<endl;
    }
    return 0;
}

Complexity

• Time complexity : O(2^n)
• Space complexity : O(n)