
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes
Principle Component Regression (PCR) is an algorithm for reducing the multi-collinearity of a dataset. The problem we face in multi-variate linear regression (linear regression with a large number of features) is that although it may appear that we do fit the model well, there is normally a high-variance problem on the test set.
PCR is basically using PCA, and then performing Linear Regression on these new PCs.
In order to prevent this degree of overfitting, PCR aims to add a slight bias, such that we are now aiming to fit the model with a slightly less training accuracy, but aim to reduce the variance to a large extent. PCR aims to achieve something very similar to what Ridge Regression tries to do. Both of these methods try to reduce overfitting, but differ in their approach.
The key idea of how PCR aims to do this, is to use PCA on the dataset before regression.
In PCR instead of regressing the dependent variable on the independent variables directly, the principal components of the independent variables are used.
Principle Component Analysis (PCA)
Principal component analysis is a method of data reduction - representing a large number of variables by a (much) smaller number, each of which is a linear combination of the original variables.
PCA is a Dimensionality Reduction technique, which basically combines 2 or more features together, in order to reduce the number of features. PCA combines features such that the features can suit the target variable in an accurate way.
The number of Principle Components that will be used, will always be less than the number of predictors or features that we have. This is because the objective of PCA is to reduce the number of features.
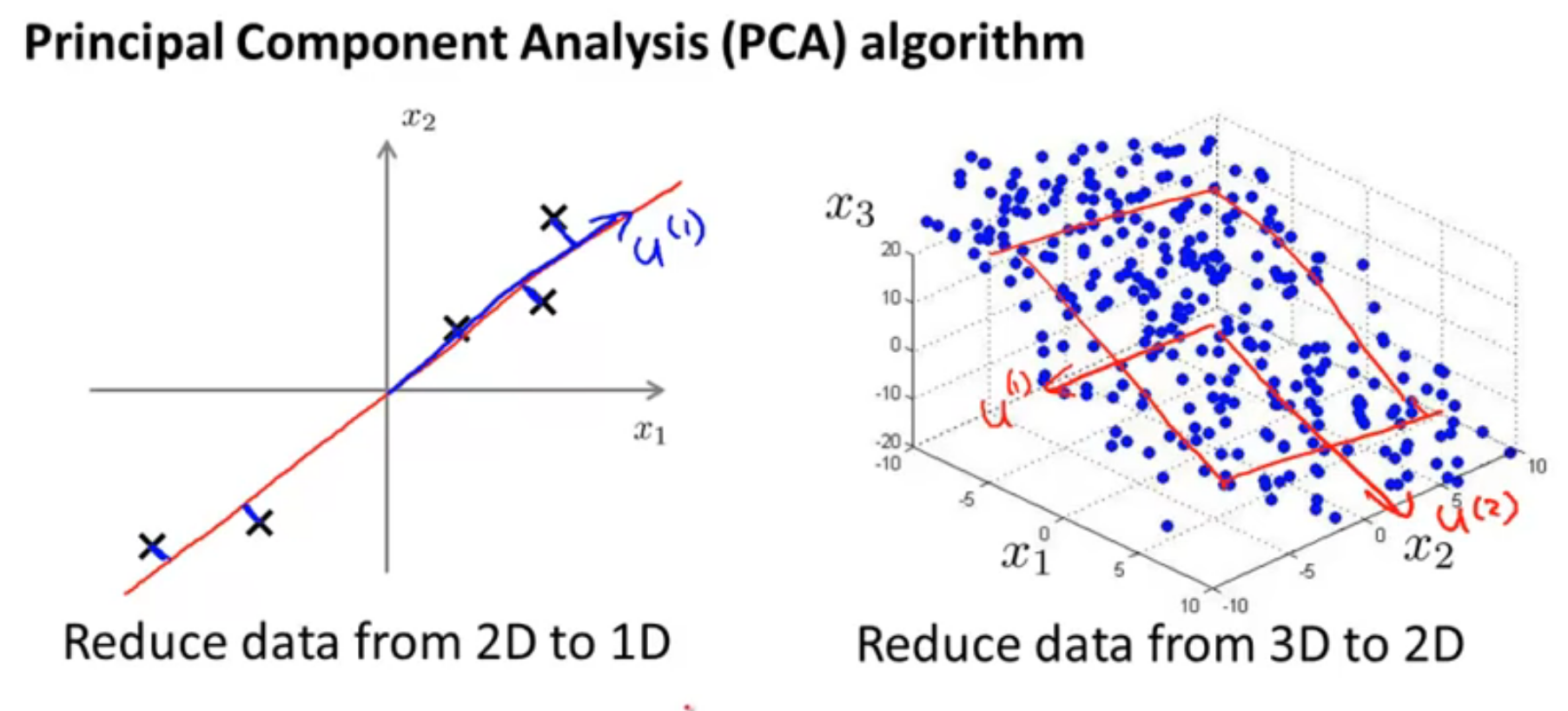
As we can see in the image above, 2D data is represented as 1D, and 3D data is represented as 2D. In both of these cases, the method of reducing the number of dimensions of the data is explained. The 'u' vectors are the new Principal Component features.
It is NOT a feature selection method, as a feature selection method would involve selecting a few features as it is, out of all of them. Instead, we are combining features to create new PCs, which are different from the original features.
Code (Simplified)
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(X_train)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
This code snippet demonstrates the procedure of transforming the higher dimensional input features, to the lower dimensional PCA features. The new X_train and X_test are having reduced number of features.
Steps of PCR:
STEP 1: Perform PCA to create PCs as our new input features
STEP 2: Use these PCs as input features to train our model for linear regression.
STEP 3: Now, we transform these PCs back to the original input features, in order to make predictions on the actual dataset.
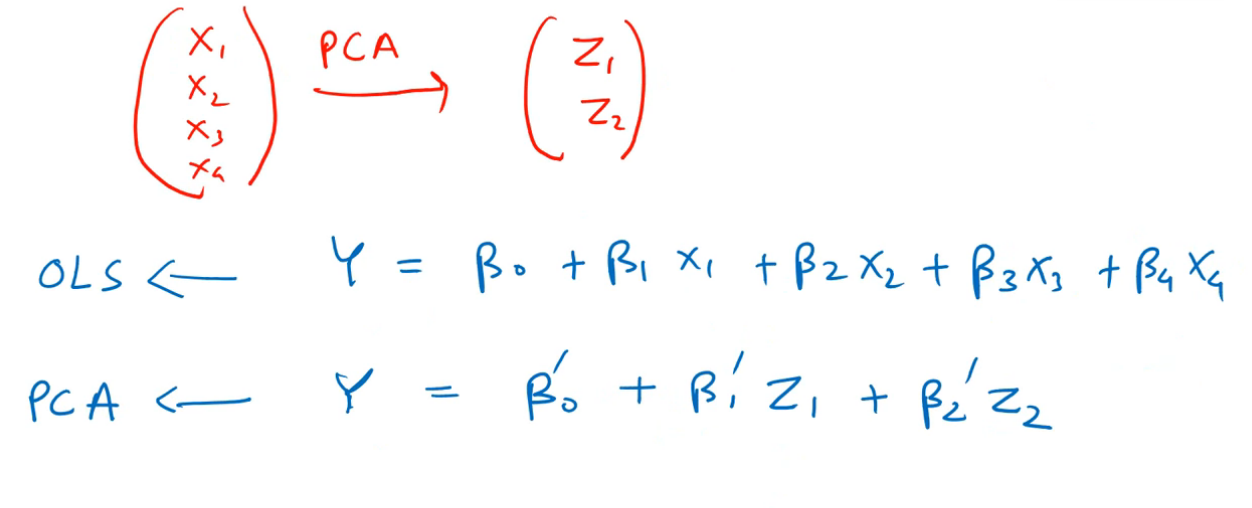
PCR is basically using PCA, and then performing Linear Regression on these new PCs. Hence, there is no significant difference in the approach used by PCR and PCA, they're essentially including the same concept.
In the above image, OLS refers to our Ordinary Least Squares regression, or Linear Regression using all of the independent variables of our dataset. We observe that there are a lot of features here, and that is our model without applying any PCA.
In the next line, we can immediately realize the effect that PCA has on our input data. The number of input features to our model are significantly reduced, which means there are new PCs created, which have the same effect on the target variable as the earlier features.
Effectively, Z1 and Z2 have the same effect on Y, as the effect of X1,X2,X3 and X4.
This is the advantage of using Principle Components.
Note that for new features (PCs), we can't use the same coefficient parameters β0 to β4. We have different coefficients now, which are in accordance with the PCs Z1 and Z2. These are represented by β'0 to β'2
Advantages of using PCR:
- PCR reduces the number of features of the model
- PCR is particularly useful on datasets facing the problem of multi-collinearity
- On datasets with highly correlated features, or even collinear features, PCR is quite useful
- PCR reduces the problem of overfitting
- Regression may take significantly lesser time because of lesser number of features
- The only decision we need to make while performing PCR is the number of input features to keep.
