
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will understand What are Sigmoid Activation Functions? And What are it’s Advantages and Disadvantages?
Table of Contents:
- Introduction
- What are Activation Functions
- Types of Activation Function
- What are Sigmoid Activation Function?
- What Is the Importance Of The Sigmoid Function In Neural Networks?
- Advantages of the Sigmoid Function
- Drawbacks of Sigmoid Function
Introduction:
The structure of a Neural Network is derived from the human brain. A Neural networks mimic the function of the human brain, allowing computer programmes to spot patterns and solve common problems. One of the decisions you have to make when designing a neural network is which activation function to implement in the hidden and output layers.
What are Activation Functions?:
Activation Function also called as transfer functions are equations that define how the weighted sum of the input of a neural node is transformed into an output.
Basically, an activation function is just a simple function that changes its inputs into outputs with a defined range. The sigmoid activation function, for example, receives input and translates the output values between 0 and 1 in a variety of ways.
If the activation function is not applied, the output signal becomes a simple linear function. A neural network without an activation function will behave like a linear regression with little learning capacity.
Types of Activation Function:
There are 2 types of Activation functions:1. Linear Activation Function
2. Non-Linear Activation Function
1. Linear Activation Function:
The neural network is reduced to just one layer using a linear activation function. When a neural network contains a linear activation function it is just a linear regression model with less power and learning capability and ability to handle different parameters of input data.
2. Non-Linear Activation Function:
The activation functions in today's neural network models are non-linear. They enable the model to produce complicated mappings between the network's inputs and outputs, which are critical for learning and modelling complex data including pictures, video, and audio, as well as non-linear or high-dimensional data sets.
Now, we will be discussing the Sigmoid Activation Function.
What are Sigmoid Activation Functions?
The sigmoid function also known as logistic function is considered as the primary choice as an activation function since it’s output exists between (0,1). As a result, it's especially useful in models that require the probability to be predicted as an output. Because the likelihood/probability, of anything, only occurs between 0 and 1, sigmoid turns out to be the best option.
Some of the properties of a Sigmoid Function are:
1. The domain of the function is from - ∞ to + ∞.
2. The function ranges from 0 to +1.
3. It is differentiable everywhere within its domain.
4. It is continuous everywhere.
5. The function is monotonic.
So, to sum it up, When a neuron's activation function is a sigmoid function, the output of this unit will always be between 0 and 1. The output of this unit would also be a non-linear function of the weighted sum of inputs, as the sigmoid is a non-linear function. A sigmoid unit is a kind of neuron that uses a sigmoid function as an activation function.
What Is The Importance Of The Sigmoid Function In Neural Networks?
When we utilize a linear activation function, we can only learn issues that are linearly separable. The addition of a hidden layer and a sigmoid function in the hidden layer, the neural network will easily understand and learn non-linearly separable problem. The non-linear function produces non-linear boundaries and thus, the sigmoid activation function can be used in neural networks to learn and understand complicated decision functions.
The mathematical representation of Sigmoid function is:
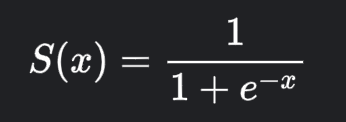
Advantages of the Sigmoid Function:
• It gives smooth gradient, thereby, preventing jumps in output values.
• It's one of the best Normalized functions out there.
• With 1 and 0, it makes a clear prediction.
• Another advantage of this function is that when used with (- infinite, + infinite) as in the linear function, it returns a value in the range of (0,1). As a result, the activation value does not disappear.
Drawbacks of Sigmoid Function:
• Vanishing gradient problem
Let’s look at what is vanishing gradient problem?
The gradients of the loss function approaches 0 when more layers with specific activation functions are added to neural networks, making the network difficult to train.
So now, let’s understand why does this happen
Certain activation functions, such as the sigmoid function, compress a wide input space into a tiny input region ranging from 0 to 1. As a result, a substantial change in the sigmoid function's input will result in a modest change in the output. As a result, the derivative shrinks.
Basically, When using gradient-based approaches to train Neural Networks, the Vanishing Gradient Problem occurs. This issue makes it difficult to learn and tune the parameters of the network's earlier layers. When training a deep neural network, you could run across the vanishing gradients problem, which is an example of unstable behaviour.
The most straightforward answer is to employ other activation functions, such as ReLU, which do not result in a small derivative.
Some other drawbacks are:
• This is not a Zero centric function
(zero centered is where the function range has 0 in the middle like a tanh function which has a range -1 to 1)
