
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article at OpenGenus, we will explore the concept of Sparse and Incremental PCA.
Table of Contents:
- Introduction
- Comparison between Sparse and Incremental PCA
- Sample calculation method
- Program for Sparse and Incremental PCA
- Applications
- Conclusion
Introduction
Principal Component Analysis (PCA) is a widely used technique for reducing the dimensionality of data. It involves finding the most significant directions of variation in a high-dimensional dataset and projecting the data onto a lower-dimensional space defined by these directions. However, for large datasets, the computational cost of computing the full PCA can be prohibitive. Sparse and Incremental Principal Component Analysis (PCA) offers an alternative approach that can be used to address this challenge.
Sparse PCA is a variant of PCA that seeks to identify the most important features or variables in a dataset and exclude the rest. By selecting only a subset of the features, sparse PCA can achieve the same level of dimensionality reduction as regular PCA but with a smaller number of features. This can be particularly useful when dealing with high-dimensional datasets where many of the features are irrelevant or redundant.
In incremental PCA, the PCA is computed incrementally as new data points are added to the dataset. This approach can be useful when dealing with streaming data or large datasets that cannot be stored in memory all at once. The incremental PCA algorithm updates the principal components based on the new data points, without the need to recompute the PCA from scratch each time.
Sparse and incremental PCA can be combined to achieve an even more efficient and scalable approach to dimensionality reduction. In this approach, the PCA is computed incrementally, and the sparse features are selected based on the updated principal components at each iteration. This allows the algorithm to adapt to changes in the dataset and to identify the most significant features as the data evolves. This approach can be particularly useful when dealing with large and evolving datasets.
Comparison between Sparse and Incremental PCA
Sparse PCA and Incremental PCA are two different approaches to Principal Component Analysis, each with its own strengths and weaknesses.
Sparse PCA is designed to identify the most important features in a dataset and exclude the rest. This approach can be particularly useful when dealing with high-dimensional datasets where many of the features are irrelevant or redundant. Sparse PCA achieves dimensionality reduction by selecting only a subset of the features, which can be a powerful tool for data compression, visualization, and analysis. However, selecting the sparse features can be a challenging problem, and the resulting PCA can be sensitive to the choice of sparsity parameters.
Incremental PCA, on the other hand, is designed to compute the PCA incrementally as new data points are added to the dataset. This approach can be particularly useful when dealing with streaming data or large datasets that cannot be stored in memory all at once. Incremental PCA updates the principal components based on the new data points, without the need to recompute the PCA from scratch each time. This can be a more efficient and scalable approach to PCA, but it may not be as accurate as computing the full PCA due to the inherent approximation of the incremental algorithm.
Sample calculations for Sparse and Incremental PCA
Performing sample calculations for Sparse and Incremental PCA requires a specific dataset and desired sparsity or increment parameters. Here is a general outline of the steps involved in each approach:
Incremental PCA:
Initialize the principal components with the first batch of data.
For each subsequent batch of data:
a. Update the covariance matrix and the principal components using the new data.
b. Project the input data onto the updated principal components to obtain the reduced-dimension representation.
Note that the specific implementation details of Sparse and Incremental PCA can vary depending on the algorithm and programming language used.
Sample Incremental PCA plot for iris dataset:
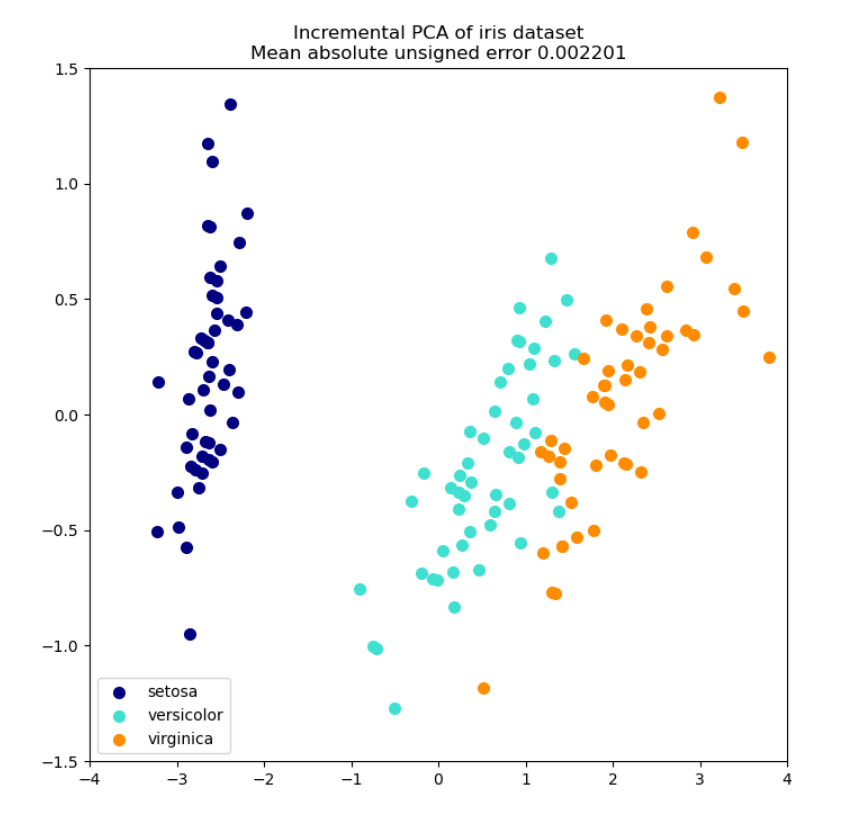
Sparse PCA:
Calculate the covariance matrix of the input data.
Use an optimization algorithm to select a subset of the features that are most important.
Calculate the principal components using the selected features.
Project the input data onto the principal components to obtain the reduced-dimension representation.
Sample Sparse PCA plot for iris dataset:
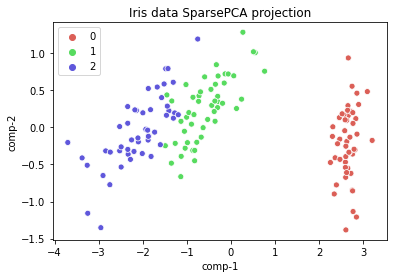
Program for sparse and Incremental PCA
Here is a sample code in Python using scikit-learn library for Sparse and Incremental PCA:
Sparse PCA:
import numpy as np
from sklearn.decomposition import SparsePCA
# dummy data
X = np.array([[-1, -1, -1], [-2, -1, 0], [-3, -2, -1], [1, 0, 1], [2, 1, 3], [3, 2, 0]])
# Initialize SparsePCA with desired sparsity parameter
spca = SparsePCA(n_components=3, alpha=0.5)
# Fit the SparsePCA model to the input data
spca.fit(X)
# Transform the input data using the fitted SparsePCA model
X_sparse = spca.transform(X)
print(X_sparse)
output:
[[-0.99009901 1.32013201 0.82508251] [-1.98019802 0.330033 0.82508251] [-2.97029703 1.32013201 1.81518152] [ 0.99009901 -0.66006601 -0.1650165 ] [ 1.98019802 -2.64026403 -1.15511551] [ 2.97029703 0.330033 -2.14521452]]
Incremental PCA:
import numpy as np
from sklearn.decomposition import IncrementalPCA
# dummy data
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
batch_size =3
# Initialize IncrementalPCA with desired increment parameter
ipca = IncrementalPCA(n_components=2)
# Process each batch of data
for batch in np.array_split(X, batch_size):
# Fit the IncrementalPCA model to the current batch of data
ipca.partial_fit(batch)
# Transform the input data using the fitted IncrementalPCA model
X_reduced = ipca.transform(X)
print(X_reduced)
output:
[[-1.38340578 -0.2935787 ] [-2.22189802 0.25133484] [-3.6053038 -0.04224385] [ 1.38340578 0.2935787 ] [ 2.22189802 -0.25133484] [ 3.6053038 0.04224385]]
Applications of Sparse and Incremental PCA
Sparse and Incremental PCA have a wide range of applications in various fields, including:
-
Image and signal processing: Sparse PCA can be used to extract meaningful features from high-dimensional images or signals, which can help with image and signal denoising, compression, and classification.
-
Bioinformatics: Sparse PCA can be used to identify relevant genes or features from high-dimensional genomic data, which can help with gene expression analysis, drug discovery, and disease diagnosis.
-
Finance: Incremental PCA can be used to monitor and analyze large financial datasets in real-time, which can help with risk management, portfolio optimization, and fraud detection.
-
Recommender systems: Sparse PCA can be used to identify latent factors or features that explain user preferences and behaviors, which can help with personalized recommendations in e-commerce and online advertising.
-
Natural language processing: Sparse PCA can be used to extract important features from high-dimensional text data, which can help with document classification, topic modeling, and sentiment analysis.
-
Computer vision: Incremental PCA can be used to perform real-time object tracking and recognition in video streams, which can help with surveillance and autonomous driving applications.
Conclusion
In conclusion, sparse and incremental PCA offer an efficient and scalable approach to dimensionality reduction that can be used to handle large datasets, streaming data, outliers, and missing data. This approach can be particularly useful in machine learning applications where high-dimensional data is common, and computational efficiency is critical. Sparse and Incremental PCA have many practical applications in a variety of fields, including image and signal processing, bioinformatics, finance, recommender systems, natural language processing, and computer vision. These techniques can help with dimensionality reduction, feature selection, and real-time processing of large and evolving datasets.
