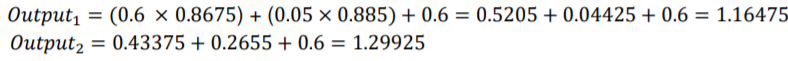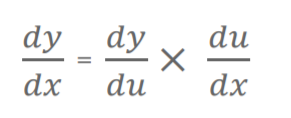Understand Neural Networks intuitively

Reading time: 30 minutes

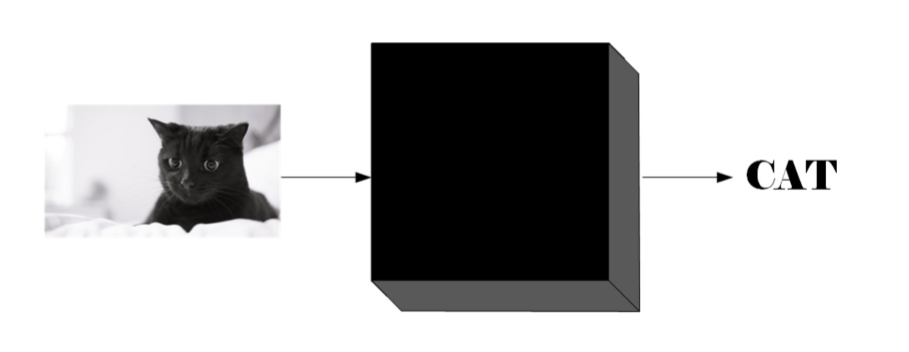
Neural Networks act as a ‘black box’ that takes inputs and predicts an output.
It’s different and ‘better’ than most traditional Machine Learning algorithms because it learns complex non-linear mappings to produce far more accurate output classification results.

A NN is a series of algorithms used to recognize relationships in a set of data through a process similar to the way human brain works. They can adapt to changing input so the network generates the best possible result without needing to redesign the output criteria. The concept of neural networks, which has its roots in artificial intelligence, is swiftly gaining popularity in the development of trading systems.

How Neural networks learn ?

Unlike other algorithms, neural networks with their deep learning cannot be programmed directly for the task. Rather, they have the requirement, just like a child’s developing brain, that they need to learn the information. The learning strategies are as follows :

• Supervised : Supervised learning is a learning technique in which we teach or train the machine using data which is well labeled that means some data is already tagged with the correct answer. After that, the machine is provided with a new set of examples so that supervised learning algorithm analyses the training data and produces a correct outcome from labeled data.

• Un-supervised : Unsupervised learning is a machine learning technique, where you do not need to supervise the model. Instead, you need to allow the model to work on its own to discover information. It mainly deals with the unlabelled data.

• Self-supervised : Self-Supervised learning refers to an approach where the labels can be generated automatically. The architecture itself and the learning process are entirely supervised but we don’t require the step of manually labeling training data.

• Reinforcement : Reinforcement Learning allows the machine or software agent to learn its behaviour based on feedback from the environment. This behaviour can be learnt once and for all, or keep on adapting as time goes by.

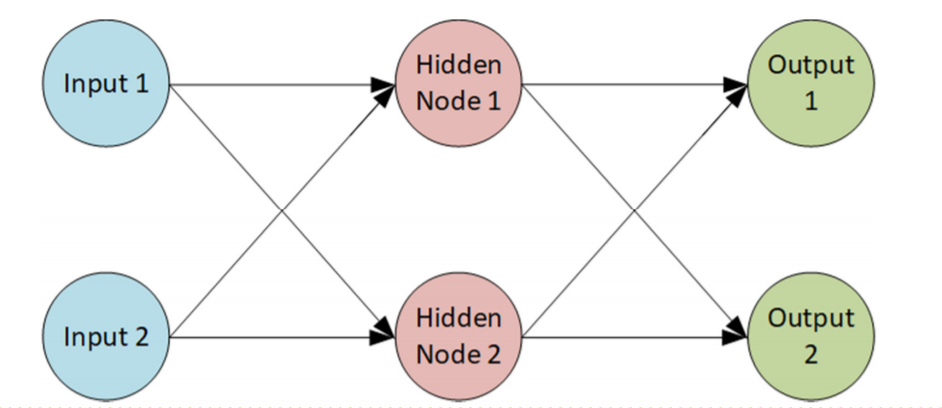
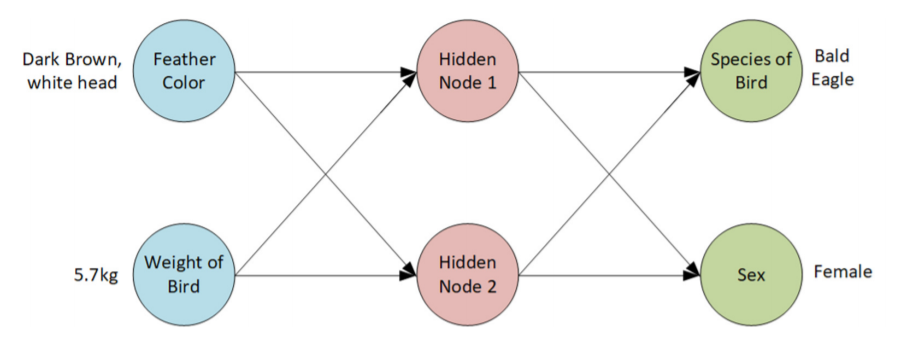
How NN looks ?

To get predictions ,just pass the input into NN to get an output.

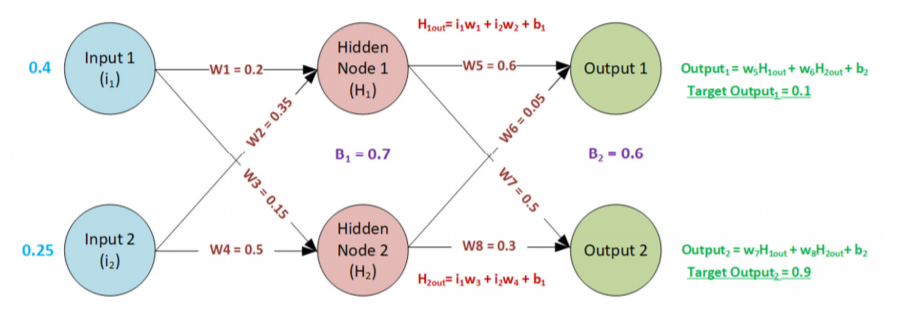
Forward Propagation

Forward propagation tells us how Neural Networks process their inputs to produce an output .

What does this tells us?

• Our initial default random weights produced very incorrect results
• Feeding numbers through a neural network is a matter of simple matrix multiplication
• Our neural network is still just a series of linear equations

Why do we have biases in the first place ?

• Biases provide every node/neuron with a trainable constant value.
• This allows us to shift the activation function output left or right.
• Changes in weights simply change the gradient or steepness of the output,
  if we need to shift our function left or right , we need a bias.

Activation Functions

Each Hidden Node is also passes through an activation function. In the simplest terms an activation function changes the output of that function.
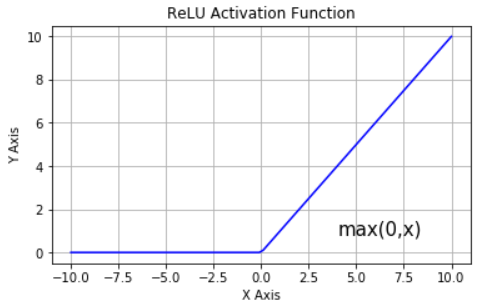
For example, let’s look a simple activation function where values below 0 are clamped to 0. Meaning negative values are changed to 0. ie. f(x) = max(0, x)

Why use Activation Functions?

• Most ML algorithms find non linear data extremely hard to model
• The huge advantage of deep learning is the ability to understand non-linear models

Example: ReLU Activation Function:
ReLU (Rectified Linear Unit) function is one of the most commonly used activation functions in training and is one of the most commonly used activation functions in training Neural Networks

• The clamping values at 0 accounts for it’s non linear behavior

More activation functions : sigmoid , hyperbolic tangent , radial basis function etc.

MoreInfo

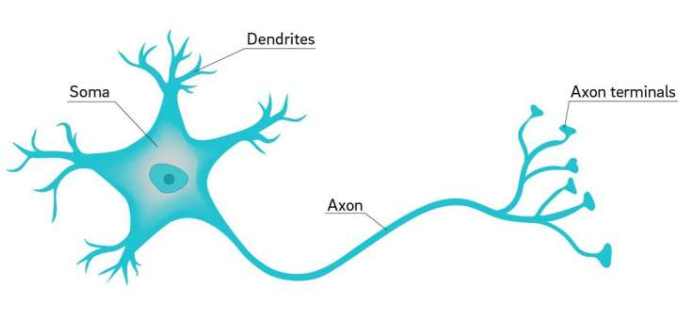
Neuron

• Neuron only fires when an input threshold is reached
• Neural Networks follow that same principle

What is 'deep' in deep learning ?

• Depth refers to the number of hidden layers
• The deeper the network, the better it learns non-linear mappings
• Deeper is always better, however there becomes a point of diminishing returns and overly long training time.
• Deeper Networks can lead to over fitting

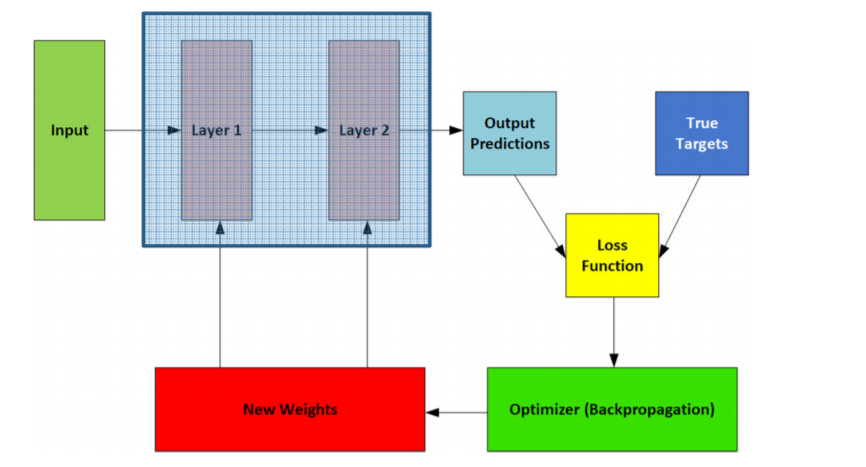
Loss funtions

These are used to determine the best 'weights' .

Steps :

1. Initialize some random values for our weights and bias
2. Input a single sample of our data
3. Compare our output with the actual value it was supposed to be, we’ll be calling this our Target values.
4. Quantify how ‘bad’ these random weights were, we’ll call this our Loss.
5. Adjust weights so that the Loss lowers
6. Keep doing this for each sample in our dataset
7. Then send the entire dataset through this weight ‘optimization’ program to see if we get an even lower loss
8. Stop training when the loss stops decreasing.

• Loss functions are integral in training Neural Nets as they measure the inconsistency or difference between the predicted results & the actual target results.
• They are always positive and penalize big errors well penalize big errors well penalize big errors well
• The lower the loss the ‘better’ the model

Types :

• L1
• L2
• Cross Entropy – Used in binary classifications
• Hinge Loss
• Mean Absolute Error (MAE)

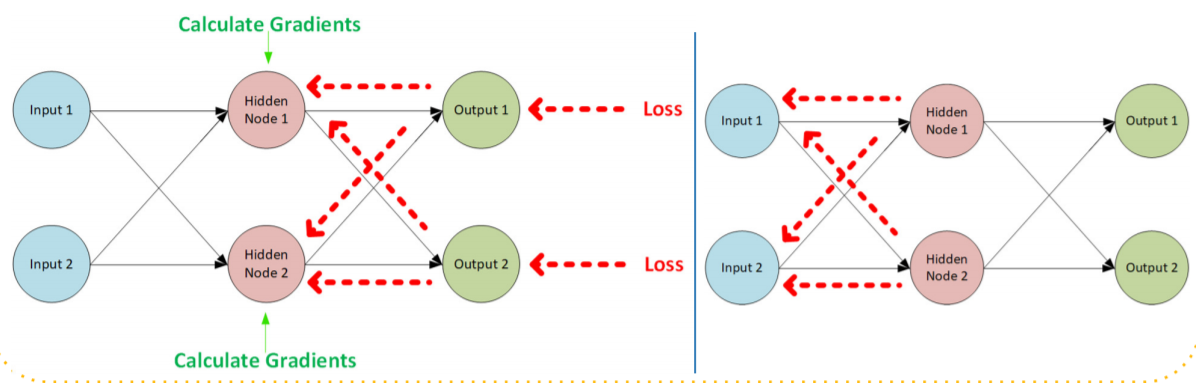
Backpropagation & Gradient Descent

Introducing Backpropagation

• What if there was a way we could use the loss to determine how to adjust the weights.
• That is the brilliance of Backpropagation

Backpropagation tells us how much would a change in each weight affect the overall loss.

Introducing Gradient Descent

• By adjusting the weights to lower the loss, we are performing gradient descent.
• Backpropagation is simply the method by which we execute gradient descent
• Gradients (also called slope) are the direction of a function at a point, it’s magnitude signifies how much the function is changing at that point.
• By adjusting the weights to lower the loss, we are performing gradient descent.
• Gradients are the direction of a function at a point

Types:

• Naive Gradient Decent is very computationally expensive/slow as it
  requires exposure to the entire dataset, then updates the gradient.
• Stochastic Gradient Descent (SGD) does the updates Stochastic Gradient Descent (SGD) after every input sample. This produces noisy or fluctuating loss outputs. However, again this method can be slow.
• Mini Batch Gradient Descent is a combination of the Mini Batch Gradient Descent two. It takes a batch of input samples and updates the gradient after that batch is processed. It leads to must faster training

The Chain Rule :

• Backpropagation is made possible by the Chain Rule.

If we have two functions y=f(u) and u=g(x) then derivatie of y is :

What makes a good model ?

• It must be accurate
• It must generalize well
• It does not overfit

To avoid overfitting generally we perform a test-train split on our data . Generally
only 70% of data is trained and other 30% is used for testing our model.
Using more deeper network can lead to overfitting as well

Regularization : making our modelmore general to our dataset .
Types : L1&L2 , cross validation , early stopping , dropout , dataset augmentation etc.

Measuring accuracy : There are many ways and factors that are used to measure accuracy . The general formula used is :
Correct classifications / total number of classifications .
But accuracy doesn't tell the whole story about a model .Some factors like F-score , recall , precision are also measured .

Applications on NN

Neural networks can be used in different fields. The tasks to which artificial neural networks are applied tend to fall within the following broad categories:

• Function approximation, or regression analysis, including time series prediction and modeling.
• Classification, including pattern and sequence recognition, novelty detection and sequential decision making.
• Data processing, including filtering, clustering, blind signal separation and compression.