An introduction to libROSA for working with audio

Reading time: 35 minutes | Coding time: 20 minutes

Librosa is powerful Python library built to work with audio and perform analysis on it. It is the starting point towards working with audio data at scale for a wide range of applications such as detecting voice from a person to finding personal characteristics from an audio.

In this article, we will learn:

• how to use Librosa and load an audio file into it
• Get audio timeline, plot it for amplitude, find tempo and pitch
• Compute mel-scaled spectrogram, time stretch an audio, remix an audio

It help us to implement:

• Audio signal analysis for music.
• Reference implementation of common methods.
• Building blocks for Music information retrieval (MIR).

For a better understanding of libROSA it is said to have a knowledge about NumPy and SciPy.

libROSA can be defined as a package which is structured as collection of submodules which further contains other functions.

For installing the libROSA you just need to run the following command in your command line:

pip install libROSA --user

In your Python code, you can import it as:

import librosa as lr

We will use Matplotlib library for plotting the results and Numpy library to handle the data as array.

Loading your audio file :

The first step towards our analysis is to load an audio library into our code. This is done using librosa.core.load() function. Audio will be automatically resampled to the given rate (default = 22050). To preserve the native sampling rate of the file, use sr=None.

librosa.core.load(path, sr=22050, mono=True, offset=0.0, duration=None, dtype=<class 'numpy.float32'>, res_type='kaiser_best')

where

• path: is the path to the audio file and is a string parameter

Any codec supported by soundfile or audioread will work. If the codec is supported by soundfile, then path can also be an open file descriptor (int), or any object implementing Python’s file interface. If the codec is not supported by soundfile (e.g., MP3), then only string file paths are supported.

• sr is the sampling rate

• mono is the option (true/ false) to convert it into mono file.

• offset is a floating point number which is the starting time to read the file

• duration is a floating point number which signifies how much of the file to load.

• dtype is the numeric representation of data can be float32, float16, int8 and others.

• res_type is the type of resampling (one option is kaiser_best)

Timeline for your audio

In this code, we will print the timeline of the audio file. We will simply load the audio, convert it into a numpy array and print the output for one sample (by dividing by sampling rate).

import numpy as np
import matplotlib.pyplot as plt 
from glob import glob
import librosa as lr


audio='arabic6' # change with the name of your audio
y, sr = lr.load('./{}.wav'.format(audio)) #you just need to make sure your audio is in the same folder in which you are coding or else you can change the path as per your requirement
time = np.arange(0,len(y))/sr
print(time) # prints timeline of arabic6

Output :

[0.00000000e+00 4.53514739e-05 9.07029478e-05 ... 2.63027211e+01
 2.63027664e+01 2.63028118e+01]

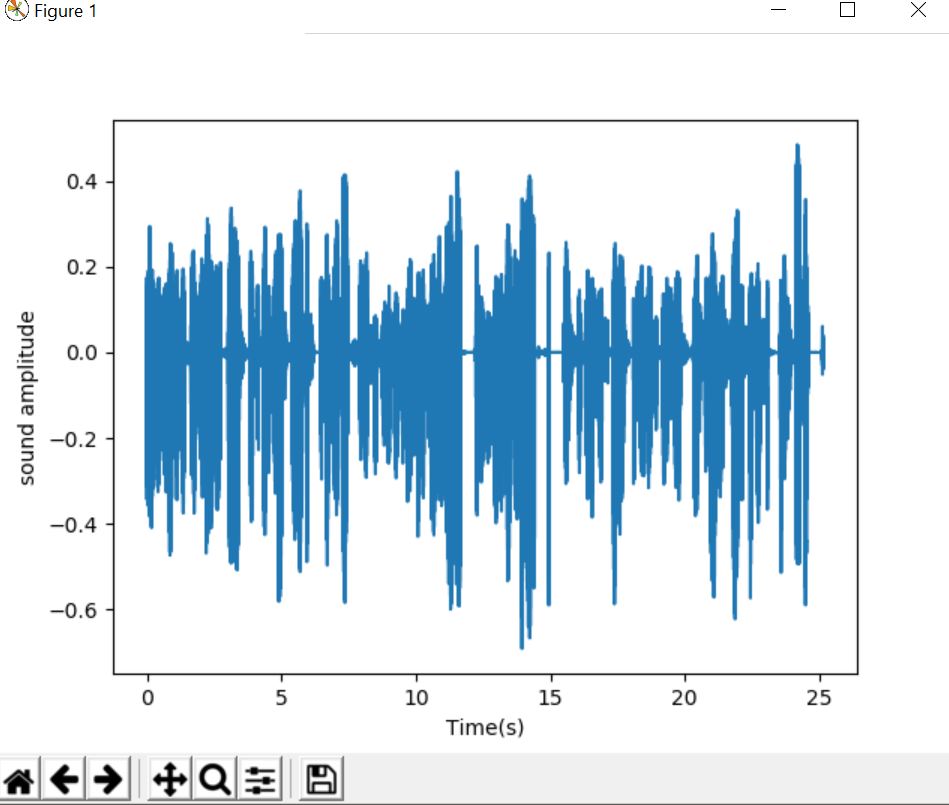
Plotting the audio :

Plotting the audio as Time v/s Sound amplitude

import numpy as np 
import matplotlib.pyplot as plt 
from glob import glob
import librosa as lr


audio='arabic6'
y, sr = lr.load('./{}.wav'.format(audio))
time = np.arange(0,len(y))/sr
fig, ax = plt.subplots()
ax.plot(time,y)
ax.set(xlabel='Time(s)',ylabel='sound amplitude')
plt.show()

Output :

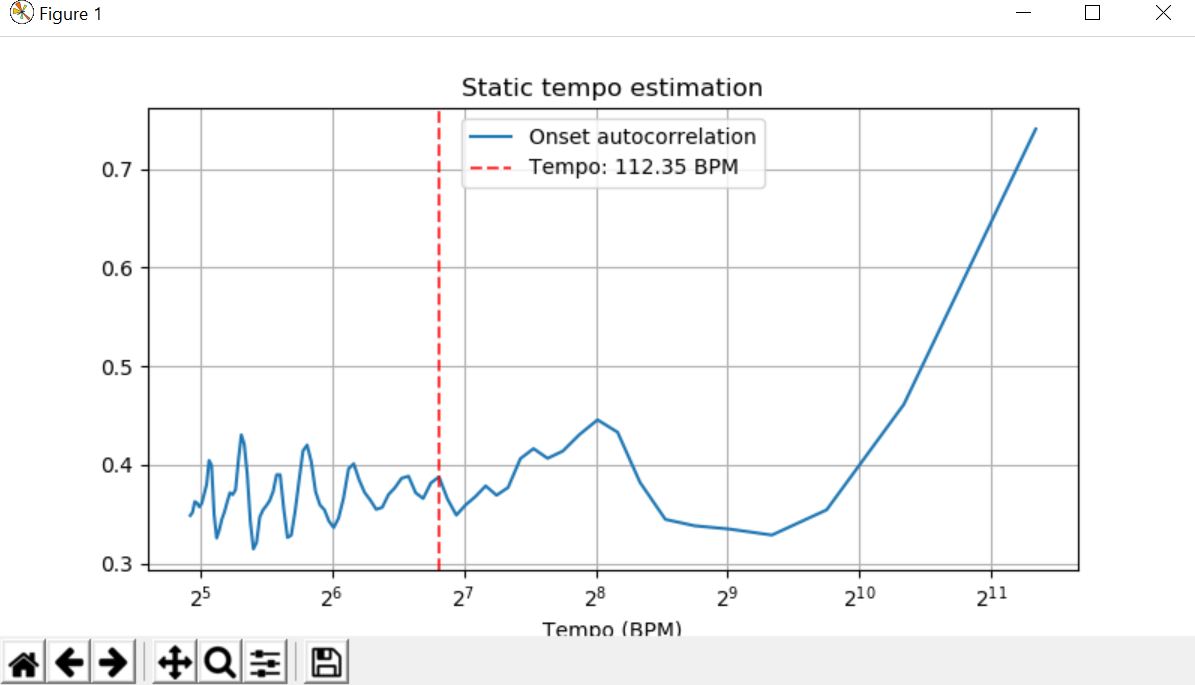
Plotting and finding the estimating tempo

Tempo was originally used to describe the timing of music, or the speed at which a piece of music is played or can be defined as beats per second.

librosa.beat.tempo(y=None, sr=22050, onset_envelope=None, hop_length=512, start_bpm=120, std_bpm=1.0, ac_size=8.0, max_tempo=320.0, aggregate=<function mean at 0x7f3faa08a510>)

It will return tempo as an array

Parameters:

• y: audio time series
• sr: sampling rate of the time series
• onset_envelope: pre-computed onset strength envelope
• hop_length: hop length of the time series
• start_bpm: initial guess of the BPM
• std_bpm: standard deviation of tempo distribution
• ac_size: length (in seconds) of the auto-correlation window
• max_tempo: estimate tempo below this threshold
• aggregate: for estimating global tempo. If None, then tempo is estimated independently for each frame.

CODE

import numpy as np 
import matplotlib.pyplot as plt 
from glob import glob
import librosa as lr

audio='arabic6'
y, sr = lr.load('./{}.wav'.format(audio))
onset_env = lr.onset.onset_strength(y, sr=sr)
tempo = lr.beat.tempo(onset_envelope=onset_env, sr=sr)
print(tempo)
tempo = np.asscalar(tempo)
# Compute 2-second windowed autocorrelation
hop_length = 512
ac = lr.autocorrelate(onset_env, 2 * sr // hop_length)
freqs = lr.tempo_frequencies(len(ac), sr=sr,hop_length=hop_length)
# Plot on a BPM axis.  We skip the first (0-lag) bin.
plt.figure(figsize=(8,4))
plt.semilogx(freqs[1:], lr.util.normalize(ac)[1:],label='Onset autocorrelation', basex=2)
plt.axvline(tempo, 0, 1, color='r', alpha=0.75, linestyle='--',label='Tempo: {:.2f} BPM'.format(tempo))
plt.xlabel('Tempo (BPM)')
plt.grid()
plt.title('Static tempo estimation')
plt.legend(frameon=True)
plt.axis('tight')
plt.show()

Output :

[112.34714674]

Finding and plotting the pitch

The sensation of a frequency is commonly referred to as the pitch of a sound. A high pitch sound corresponds to a high frequency sound wave and a low pitch sound corresponds to a low frequency sound wave.

librosa.core.piptrack(y=None, sr=22050, S=None, n_fft=2048, hop_length=None, fmin=150.0, fmax=4000.0, threshold=0.1, win_length=None, window='hann', center=True, pad_mode='reflect', ref=None)

Paramters :

• y: audio signal

• sr: audio sampling rate of y

• S: magnitude or power spectrogram

• n_fft: number of FFT bins to use, if y is provided.

• hop_length: number of samples to hop

• threshold: A bin in spectrum S is considered a pitch when it is greater than threshold * ref(S).

• fmin: lower frequency cutoff.

• fmax: upper frequency cutoff.

• win_length: Each frame of audio is windowed by window().

• ref:scalar or callable for pitch

It returns:

• pitches:np.ndarray [shape=(d, t)]
• magnitudes:np.ndarray [shape=(d,t)]
  Where d is the subset of FFT bins within fmin and fmax.

pitches[f, t] contains instantaneous frequency at bin f, time t

magnitudes[f, t] contains the corresponding magnitudes.

Both pitches and magnitudes take value 0 at bins of non-maximal magnitude.

CODE

import numpy as np 
import matplotlib.pyplot as plt 
from glob import glob
import librosa as lr
from IPython.display import Audio

audio='arabic6'
y, sr = lr.load('./{}.wav'.format(audio))
pitches, magnitudes = lr.piptrack(y=y, sr=sr)
print(pitches)
print('///')
print(magnitudes)
plt.subplot(212)
plt.show()
plt.plot(pitches)
plt.show()

Output :

[[0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 ...
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]]
///
[[0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 ...
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]]

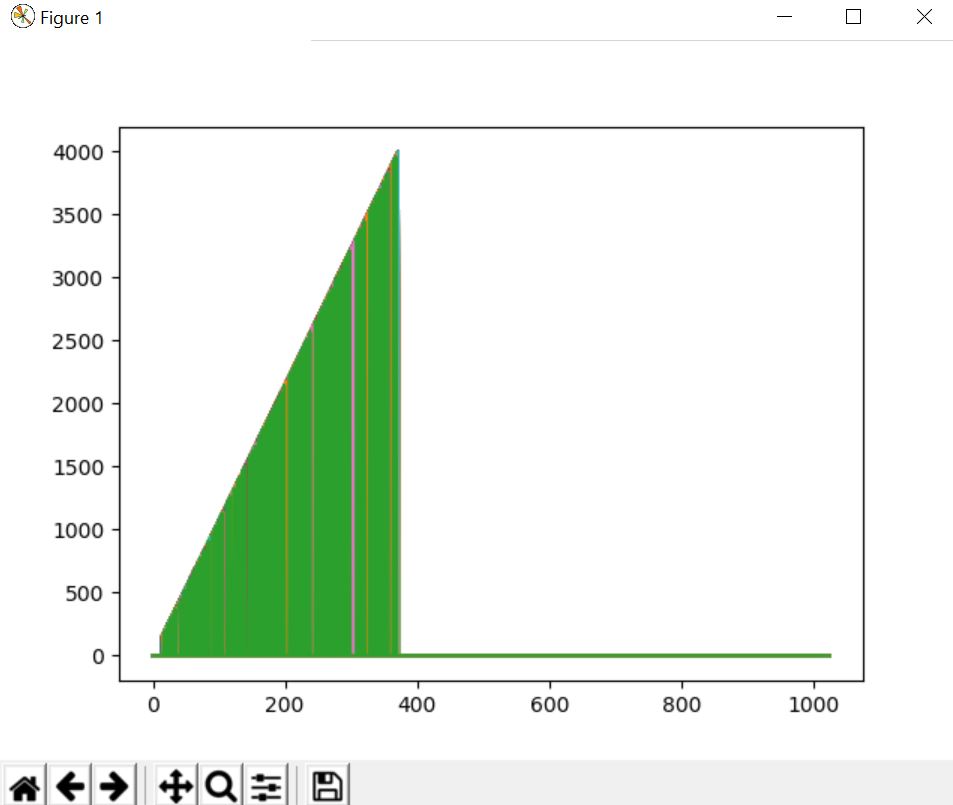
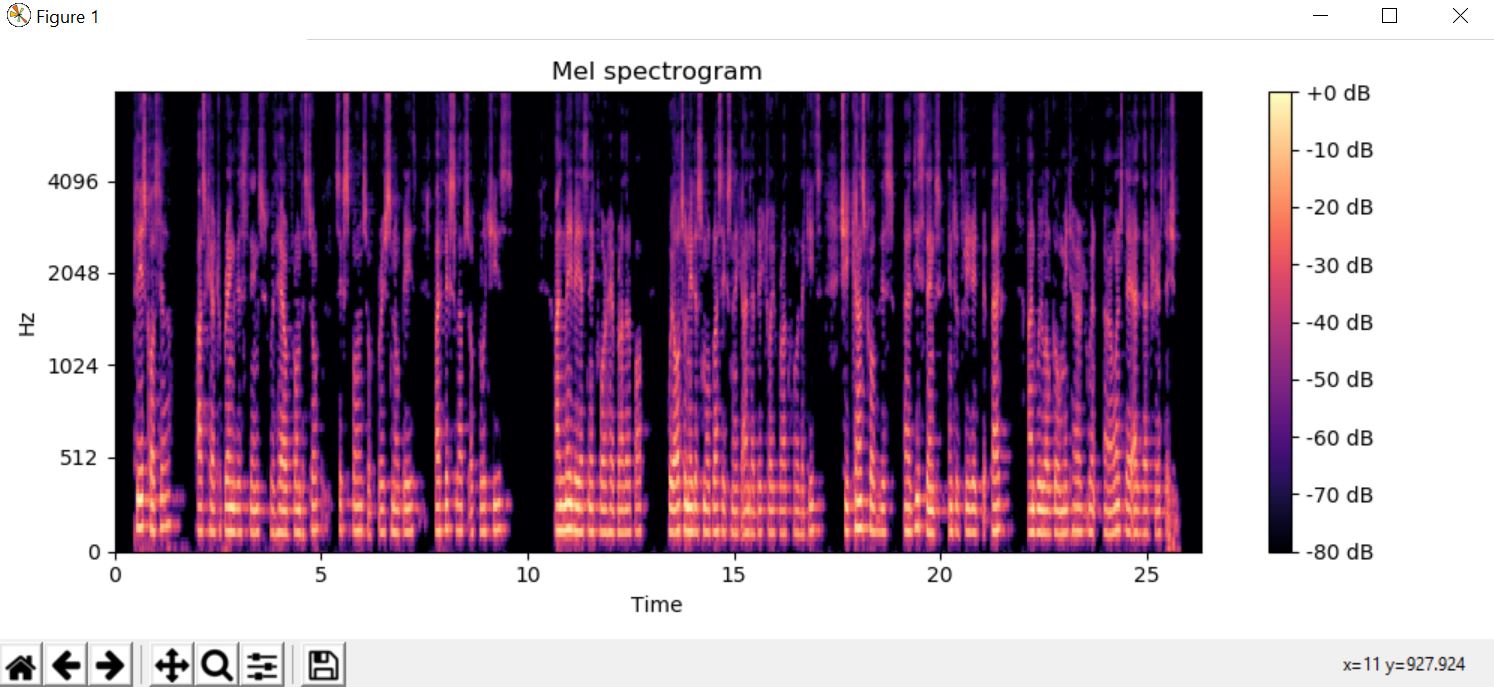
Compute a mel-scaled spectrogram

An object of type MelSpectrogram represents an acoustic time-frequency representation of a sound

librosa.feature.melspectrogram(y=None, sr=22050, S=None, n_fft=2048, hop_length=512, win_length=None, window='hann', center=True, pad_mode='reflect', power=2.0, **kwargs)

Parammeters :

• y: audio time-series

• sr: sampling rate of y

• S: spectrogram

• n_fft: length of the FFT window

• hop_length: number of samples between successive frames. See librosa.core.stft

• win_length: Each frame of audio is windowed by window().

• power: Exponent for the magnitude melspectrogram. e.g., 1 for energy, 2 for power, etc.

• kwargs:additional keyword arguments
  Mel filter bank parameters. See librosa.filters.mel for details.

Returns:

• S:np.ndarray [shape=(n_mels, t)]
  Mel spectrogram

CODE

import numpy as np 
import matplotlib.pyplot as plt 
from glob import glob
import librosa as lr
import librosa.display
audio='arabic6'
y, sr = lr.load('./{}.wav'.format(audio))
lr.feature.melspectrogram(y=y, sr=sr)

D = np.abs(lr.stft(y))**2
S = lr.feature.melspectrogram(S=D)
S = lr.feature.melspectrogram(y=y, sr=sr, n_mels=128,fmax=8000)
plt.figure(figsize=(10, 4))
lr.display.specshow(lr.power_to_db(S,ref=np.max),y_axis='mel', fmax=8000,x_axis='time')
plt.colorbar(format='%+2.0f dB')
plt.title('Mel spectrogram')
plt.tight_layout()
plt.show()

Output :

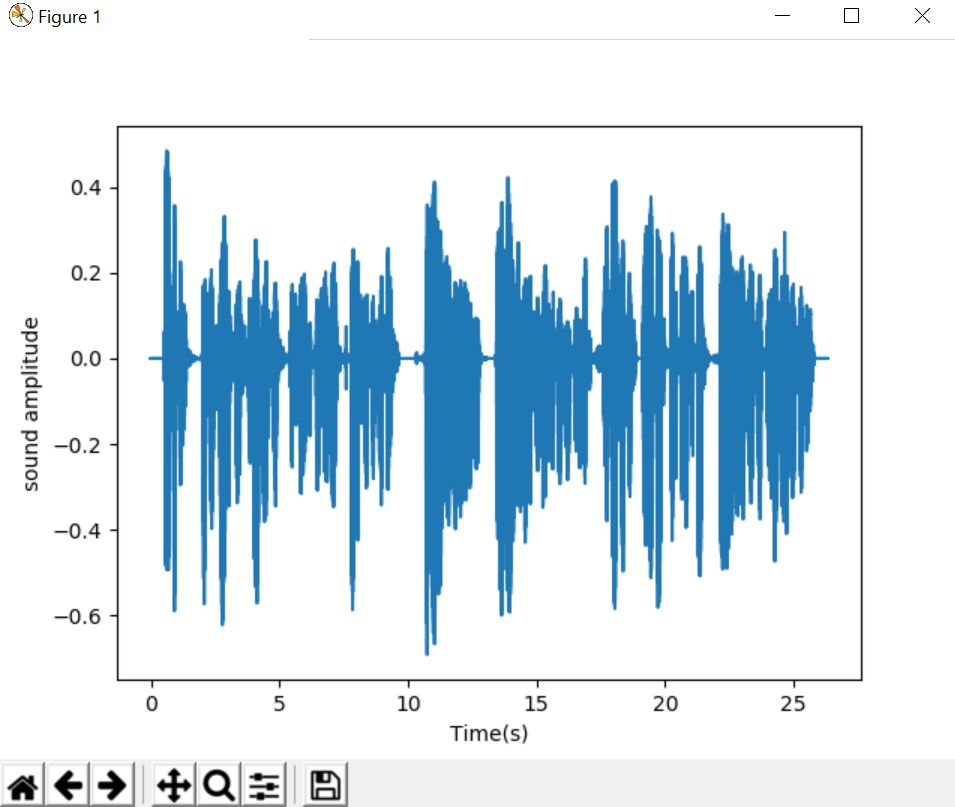
Modifying the audio :

Time-stretch an audio series by a fixed rate

librosa.effects.time_stretch(y, rate, **kwargs)

Parameters:

• y: audio time series
• rate: Stretch factor. If rate > 1, then the signal is sped up. If rate < 1, then the signal is slowed down.
• kwargs: additional keyword arguments.
  See librosa.decompose.stft for details.

Returns:

• y_stretch: audio time series stretched by the specified rate

CODE

import numpy as np 
import matplotlib.pyplot as plt 
from glob import glob
import librosa as lr

audio='arabic6'
y, sr = lr.load('./{}.wav'.format(audio))
y_fast = lr.effects.time_stretch(y, 2.0)
time = np.arange(0,len(y_fast))/sr
fig, ax = plt.subplots()
ax.plot(time,y_fast)
ax.set(xlabel='Time(s)',ylabel='sound amplitude')
plt.show()#compress to be twice as fast

y_slow = lr.effects.time_stretch(y, 0.5)
time = np.arange(0,len(y_slow))/sr
fig, ax = plt.subplots()
ax.plot(time,y_slow)
ax.set(xlabel='Time(s)',ylabel='sound amplitude')
plt.show()#half the original speed

Output :

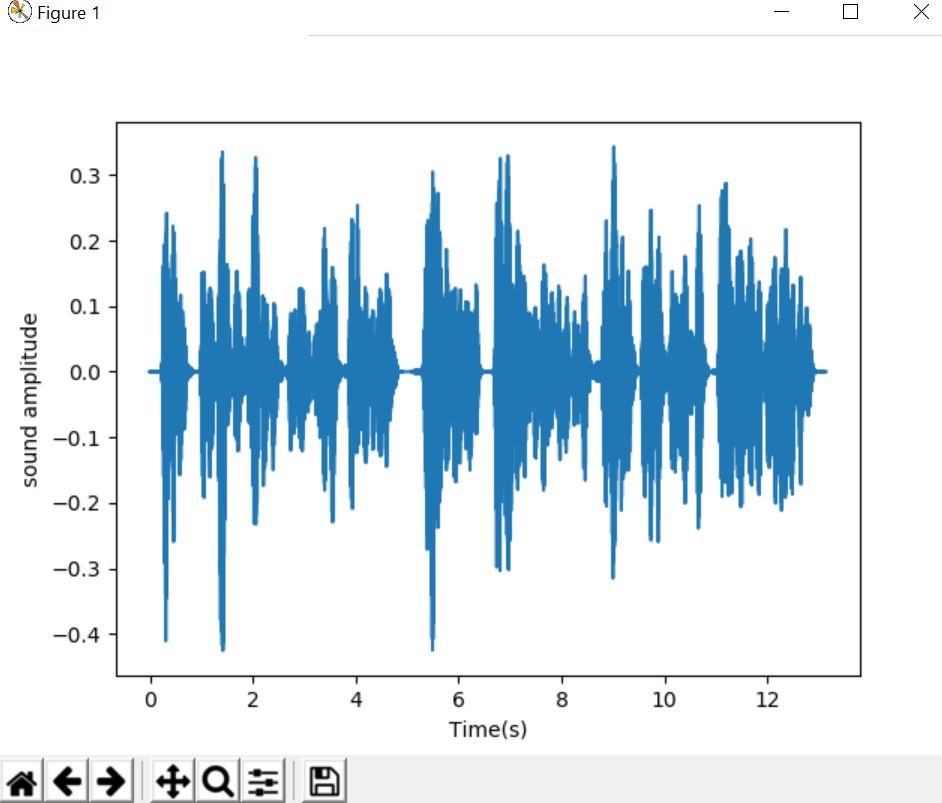
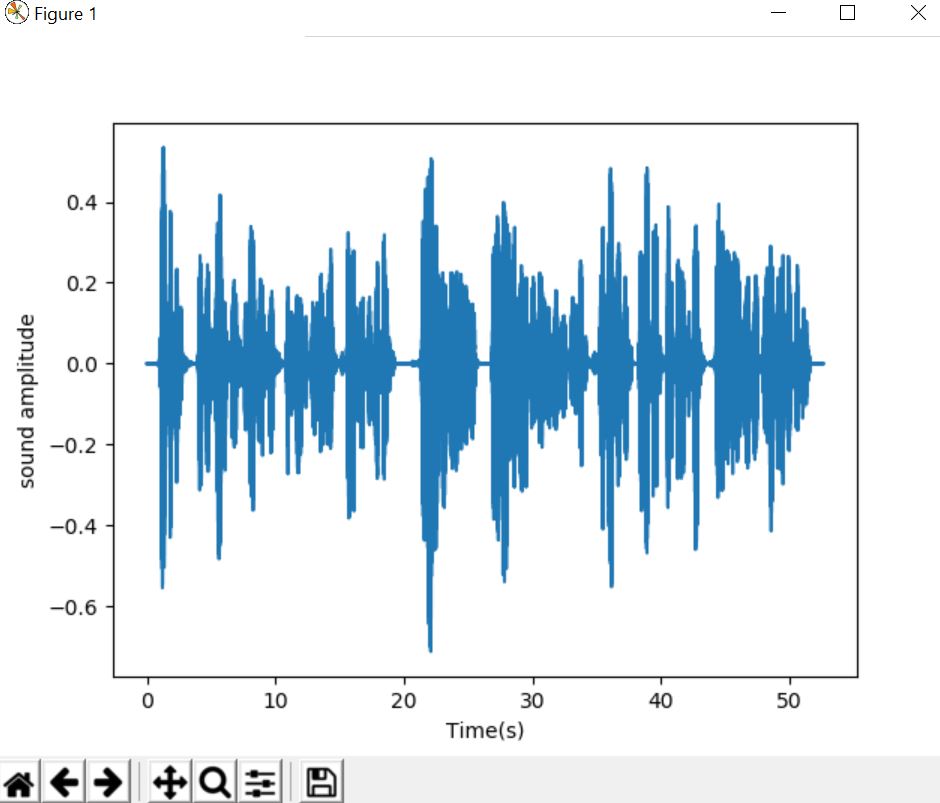
Remix an audio signal by re-ordering time intervals

Remix is a piece of media which has been altered from its original state by adding, removing and changing pieces of the item. A song, piece of artwork, books, video, or photograph can all be remixes. The only characteristic of a remix is that it appropriates and changes other materials to create something new.

librosa.effects.remix(y, intervals, align_zeros=True)

Parameters :

• y: Audio time series

• intervals: iterable of tuples (start, end)
  An iterable (list-like or generator) where the ith itemintervals[i] indicates the start and end (in samples) of a slice of y.

• align_zeros: boolean
  If True, interval boundaries are mapped to the closest zero-crossing in y. If y is stereo, zero-crossings are computed after converting to mono.

Returns:

• y_remix:np.ndarray [shape=(d,) or (2, d)]
• y remixed in the order specified by intervals

CODE

import numpy as np 
import matplotlib.pyplot as plt 
from glob import glob
import librosa as lr

audio='arabic6'
y, sr = lr.load('./{}.wav'.format(audio))
_, beat_frames = lr.beat.beat_track(y=y, sr=sr,hop_length=512)
beat_samples = lr.frames_to_samples(beat_frames)
intervals = lr.util.frame(beat_samples, frame_length=2,hop_length=1).T
y_out = lr.effects.remix(y, intervals[::-1])
time = np.arange(0,len(y_out))/sr
fig, ax = plt.subplots()
ax.plot(time,y_out)
ax.set(xlabel='Time(s)',ylabel='sound amplitude')
plt.show()

Output :