Table of content:

1. Introduction to selection sort
2. Selection Sort in Python: OOP-based
   • Attributes
   • Methods
   • Implementation
3. Approaches to implement Selection sort
4. Time and Space Complexity
5. Application
6. Questions

Introduction to selection sort

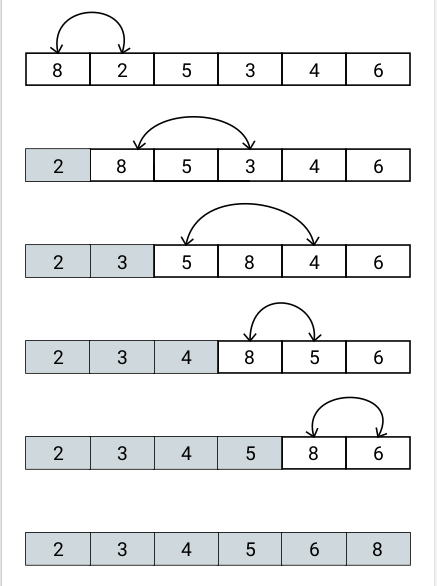
Selection sort is a basic sorting algorithm applied to a list. It works by repeatedly finding the smallest element from the unsorted part of the list and swapping it with the first element. This process continues until the entire list is sorted. At each iteration, the algorithm identifies the smallest element in the unsorted portion and places it at the correct position in the sorted section.

Here is a step-by-step explanation of how selection sort works:

• Find the smallest (or largest) element in the unsorted part of the list.
• Swap the smallest (or largest) element with the leftmost element of the unsorted part.
• Move the boundary between the sorted and unsorted parts one element to the right.
• Repeat steps 1-3 until the unsorted part becomes empty.

Selection Sort in Python: OOP-based

To implement selection sort in Python using an object-oriented approach, we can create a class called SelectionSort that encapsulates the functionality of the sorting algorithm. This class will consist of methods and attributes necessary to perform the sorting operation efficiently. By encapsulating the sorting logic within a class, we can achieve code reusability and enhance the overall readability of the code. The class will have the following attributes and methods:

Attributes:

• data: A list containing the elements to be sorted.

Methods:

• init(self, data): A constructor method that initializes the data attribute with the input.
• sort(self): A method that performs the selection sort algorithm on the data attribute.
• Display(self): This method is used to display sorted array

Implementation:

class SelectionSort:

    # methods
    def __init__(self, LIST):
        self.LIST = LIST
    
    def sort(self):
        for i in range(0, len(self.LIST)):
            min_index = i
            for j in range(i+1, len(self.LIST)):
                if LIST[j] < LIST[min_index]:
                    min_index = j
            self.LIST[i], self.LIST[min_index] = self.LIST[min_index], self.LIST[i]

        
    def print_LIST(self):
        for i in range(len(self.LIST)):
            print(self.LIST[i], end=" ")



# Driver code
LIST = [10, 5, 2, 3, 1, 8, 9, 7, 6]

# Object instantiation
Selection_Sort = SelectionSort(LIST)
Selection_Sort.sort()
print("Sorted List:")
Selection_Sort.print_LIST()


"""
Output: 
Sorted List:
1 2 3 5 6 7 8 9 10
"""

By implementing selection sort using object-oriented programming (OOP) concepts, the algorithm's workings become more comprehensible. The resulting code becomes modular and reusable, facilitating easier maintenance and extension of functionality.

Approaches to implement Selection sort

There are two main approaches to implement selection sort in Python:

Recursive approach: In the recursive approach, the selection sort algorithm utilizes recursion to find the minimum element in the array. A recursive function is employed, which takes the array as an input and returns the sorted array as output. Within the recursive function, the minimum element is found and placed at the appropriate position in the sorted portion of the array. The recursion continues with the remaining unsorted portion until the entire array is sorted. This recursive approach provides an alternative implementation of selection sort and can be useful in certain programming contexts.

Iterative approach: In the iterative approach of selection sort, a loop is used to iterate through the array. During each iteration, the minimum element in the unsorted portion of the array is identified. This minimum element is then swapped with the element at the current index. This process continues until all the elements in the array have been sorted, resulting in an ascending order of elements.

A class-based implementation of the selection sort algorithm with parent and child classes

Please follow the step-by-step process below:

• Define a parent class called Sort with a method named selection_sort.

class Sort:
    def selection_sort(self, LIST):
        for i in range(len(LIST)):
            min_index = i
            for j in range(i + 1, len(LIST)):
                if LIST[j] < LIST[min_index]:
                    min_index = j

            LIST[i], LIST[min_index] = LIST[min_index], LIST[i]

        return LIST

• Create a child class named RecursiveSort that inherits from the Sort class and implements the recursive version of the selection sort algorithm.

class RecursiveSort(Sort):
    def selection_sort(self, LIST):
        if len(LIST) <= 1:
            return LIST

        min_index = 0
        for i in range(1, len(LIST)):
            if LIST[i] < LIST[min_index]:
                min_index = i

        LIST[0], LIST[min_index] = LIST[min_index], LIST[0]
        return [LIST[0]] + self.selection_sort(LIST[1:])

• Create another child class named IterativeSort that inherits from the Sort class and implements the iterative version of the selection sort algorithm.

class IterativeSort(Sort):
    def selection_sort(self, LIST):
        for i in range(len(LIST)):
            min_index = i
            for j in range(i + 1, len(LIST)):
                if arr[j] < arr[min_index]:
                    min_index = j

            LIST[i], LIST[min_index] = LIST[min_index], LIST[i]

        return LIST

• Use the class by creating objects and calling the selection_sort method.

# Using the Sort class
sort_obj = Sort()
sorted_list = sort_obj.selection_sort(arr)
print("Sorted List (Sort class):", sorted_list)

# Using the RecursiveSort class
recursive_sort_obj = RecursiveSort()
sorted_list_recursive = recursive_sort_obj.selection_sort(arr)
print("Sorted List (RecursiveSort class):", sorted_list_recursive)

# Using the IterativeSort class
iterative_sort_obj = IterativeSort()
sorted_list_iterative = iterative_sort_obj.selection_sort(arr)
print("Sorted List (IterativeSort class):", sorted_list_iterative)

Final Implementation

class Sort:
    def selection_sort(self, LIST):
        for i in range(len(LIST)):
            min_index = i
            for j in range(i + 1, len(LIST)):
                if LIST[j] < LIST[min_index]:
                    min_index = j

            LIST[i], LIST[min_index] = LIST[min_index], LIST[i]

        return LIST


class RecursiveSort(Sort):
    def selection_sort(self, LIST):
        if len(LIST) <= 1:
            return LIST

        min_index = 0
        for i in range(1, len(LIST)):
            if LIST[i] < LIST[min_index]:
                min_index = i

        LIST[0], LIST[min_index] = LIST[min_index], LIST[0]
        return [LIST[0]] + self.selection_sort(LIST[1:])


class IterativeSort(Sort):
    def selection_sort(self, LIST):
        for i in range(len(LIST)):
            min_index = i
            for j in range(i + 1, len(LIST)):
                if arr[j] < arr[min_index]:
                    min_index = j

            LIST[i], LIST[min_index] = LIST[min_index], LIST[i]

        return LIST


# Usage example
arr = [10, 5, 2, 3, 1, 8, 9, 7, 6]

# Using the Sort class
sort_obj = Sort()
sorted_list = sort_obj.selection_sort(arr)
print("Sorted List (Sort class):", sorted_list)

# Using the RecursiveSort class
recursive_sort_obj = RecursiveSort()
sorted_list_recursive = recursive_sort_obj.selection_sort(arr)
print("Sorted List (RecursiveSort class):", sorted_list_recursive)

# Using the IterativeSort class
iterative_sort_obj = IterativeSort()
sorted_list_iterative = iterative_sort_obj.selection_sort(arr)
print("Sorted List (IterativeSort class):", sorted_list_iterative)

"""
Output:
Sorted List (Sort class): [1, 2, 3, 5, 6, 7, 8, 9, 10]
Sorted List (RecursiveSort class): [1, 2, 3, 5, 6, 7, 8, 9, 10]
Sorted List (IterativeSort class): [1, 2, 3, 5, 6, 7, 8, 9, 10]

Time and Space Complexity

The time complexity of selection sort in Python using OOP is O(n^2), where n is the number of elements in the array. This is because the algorithm involves nested loops, where the outer loop runs n times and the inner loop runs n-i times, where i is the current index of the outer loop. Therefore, the total number of comparisons is (n-1) + (n-2) + ... + 1, which is equal to n(n-1)/2, or O(n^2).

The space complexity of selection sort in Python using OOP is O(1), which means that it is constant and does not depend on the size of the input array. This is because the algorithm sorts the array in place, without using any additional data structures. The only extra space used is for the variables used in the loops, which are constant and do not depend on the size of the input array.

Application

Selection sort finds its main application in educational settings and scenarios involving small datasets. Its simplicity and ease of implementation make it an ideal algorithm for introducing students to sorting concepts. However, when dealing with larger datasets, selection sort tends to be less efficient compared to more advanced sorting algorithms like merge sort, quicksort, or heapsort, which offer superior time complexities.

Despite its limitations, selection sort remains a valuable tool in certain situations. It is a straightforward and easy-to-understand algorithm, making it useful for beginners and those seeking a basic understanding of sorting techniques. Its simplicity allows for quick implementation and can be beneficial when sorting small datasets or arrays where the overhead of more complex algorithms outweighs the benefits.

Moreover, selection sort performs reasonably well when confronted with partially sorted lists, as it only makes the necessary number of swaps required to achieve a sorted order.
However, it is important to note that when dealing with larger datasets or applications where efficiency is crucial, selection sort may not be the optimal choice.

Algorithms like merge sort or quicksort, with their better time complexities, are more suitable for such scenarios. These advanced sorting algorithms provide faster and more efficient sorting, even when confronted with large datasets. Therefore, while selection sort serves as a valuable learning tool and can be beneficial in certain specific cases, it is generally recommended to utilize more advanced sorting algorithms for practical applications.

Questions

Discover various sorting algorithms through this informative link