Different Basic Sorting algorithms. Know when to use which one and Ace your tech interview!

Who doesn't want to get their dream job? But only few are able to crack it successfully. There are so many things to look into when you are going to face the technical interview but one should definitely have the strong understanding of basic sorting algorithms to stay confident and perform better than your competitors.

This is not only for those who are preparing for interviews but this is helpful when we are attending competitive programming contests. Go ahead and read the complete article dear learner :)

What are sorting algorithms used for?

We all have heard the term 'sorting' and it basically means to arrange the elements of a collection(ex- array or linked list etc) in some specific order (ex- ascending or descending etc).The algorithms used for the implementation of sorting are called sorting algorithms.

We are going to take a close look at selection sort, bubble sort, insertion sort, merge sort and quick sort and the respective basic definition ,example, algorithm, analysis of algorithm and when do we apply it.

Time complexity and Space complexity

• Time complexity is a function describing the amount of time an algorithm takes in terms of the amount of input to the algorithm.
• Space complexity is a function describing the amount of memory (space) an algorithm takes in terms of the amount of input to the algorithm.

What are in-place sorting algorithms?

• An in-place algorithm is the one that does not need any extra space and produces an output in the same memory that contains the input data.This reduces the cost.
• Many sorting algorithms rearrange arrays into sorted order in-place, including: bubble sort, comb sort, selection sort, insertion sort, heapsort, and Shell sort. These algorithms require only a few pointers.
• Quicksort operates in-place on the data to be sorted.

Let's discuss the algorithms one by one.

1. Selection Sort

The selection sort algorithm sorts an array by repeatedly finding the minimum element from unsorted part and putting it at the beginning. The algorithm maintains two subarrays in a given array i.e subarray which is sorted and subarray which is unsorted.

let's understand with an example:

Algorithm for selection sort

ALGORITHM SelectionSort(A[0..n − 1])
//Sorts a given array by selection sort
//Input: An array A[0..n − 1] of orderable elements
//Output: Array A[0..n − 1] sorted in nondecreasing order
for i ← 0 to n − 2 do
    min ← i
    for j ← i + 1 to n − 1 do
        if A[j ] < A[min] min ← j
    swap A[i] and A[min]

Quick Analysis
Two for loops are used in selection sort:

• one for storing the min index which changes in each iteration
• second loop for traversing through the subarray
  Best, average and worst case time complexity: n^2 . This remains same independent of distribution of data.

When to use selection sort?

• When the list is small. As the time complexity of selection sort is O(N^2) which makes it inefficient for a large list.
• When memory space is limited because it makes the minimum possible number of swaps during sorting.Selection sort never makes more than O(n) swaps.

2. Bubble sort

Bubble sort is the simplest sorting algorithm and the logic used is really simple. It works by repeatedly swapping the adjacent elements if they are in the wrong order, which is found out when compared. If we have total N elements, then we need to repeat the above process for N-1 times.

Let's understand with an example:

Algorithm for bubble sort

ALGORITHM BubbleSort(A[0..n − 1])
//Sorts a given array by bubble sort
//Input: An array A[0..n − 1] of orderable elements
//Output: Array A[0..n − 1] sorted in nondecreasing order
for i ← 0 to n − 2 do
    for j ← 0 to n − 2 − i do
        if A[j] > A[j + 1] 
            swap A[j ] and A[j + 1]

Quick Analysis

• From the pseudocode we can see that two for loops are used for traversing along the array and sorting it
• Worst and Average Case Time Complexity: O(n*n). Worst case occurs when array is reverse sorted.
• Best Case Time Complexity: O(n). Best case occurs when array is already sorted.

When to use bubble sort?

• Bubble sort algorithm works well with large datasets where the items are almost sorted because it takes only one iteration to detect whether the list is sorted or not.
• if the list is unsorted to a large extend then this algorithm holds good for collections of less number of elements.
• Bubble sort is fastest on an extremely small or nearly sorted set of data.

3. Insertion Sort

This sorting algorithm is a simple sorting algorithm that works the way we sort playing cards in our hands. The array is seen to be split into a sorted and an unsorted part. Algorithm then places an unsorted element at its suitable place at sorted array in each iteration.

Let's understand with an example:

Algorithm for insertion sort

ALGORITHM InsertionSort(A[0..n − 1])
//Sorts a given array by insertion sort
//Input: An array A[0..n − 1] of n orderable elements
//Output: Array A[0..n − 1] sorted in nondecreasing order
for i ← 1 to n − 1 do
    v ← A[i]
    j ← i − 1
    while j ≥ 0 and A[j] > v do
        A[j + 1]← A[j ]
        j ← j − 1
    A[j + 1] ← v

Quick Analysis

• We can see that there are 2 loops one for loop and another while loop which are used for initializing key and traversing through unsorted subarray resp.
• Average and worst case time complexity: n^2
• Best case time complexity: n when array is already sorted.
• Worst case: when the array is reverse sorted.

When to use insertion sort?

• It is not advised to apply insertion sort when elements are in reverse order. In that case insertion sort takes maximum time to sort.
• When the elements are sorted it takes the minimum time i.e O(N).If the data is almost sorted or when the list is small as it has a complexity of O(N^2).If the list is sorted a minimum number of elements will slide over to insert the element at it's correct location i.e at sorted array part.
• Algorithm is stable and it has fast running case when the list is nearly sorted.

Merge Sort

Merge sort algorithm is based on Divide and Conquer algorithm. It divides input array into two halves, calls itself for the two halves, sorting each of them recursively, and then merging the two smaller sorted arrays into a single sorted one.

Let's understand with an example :

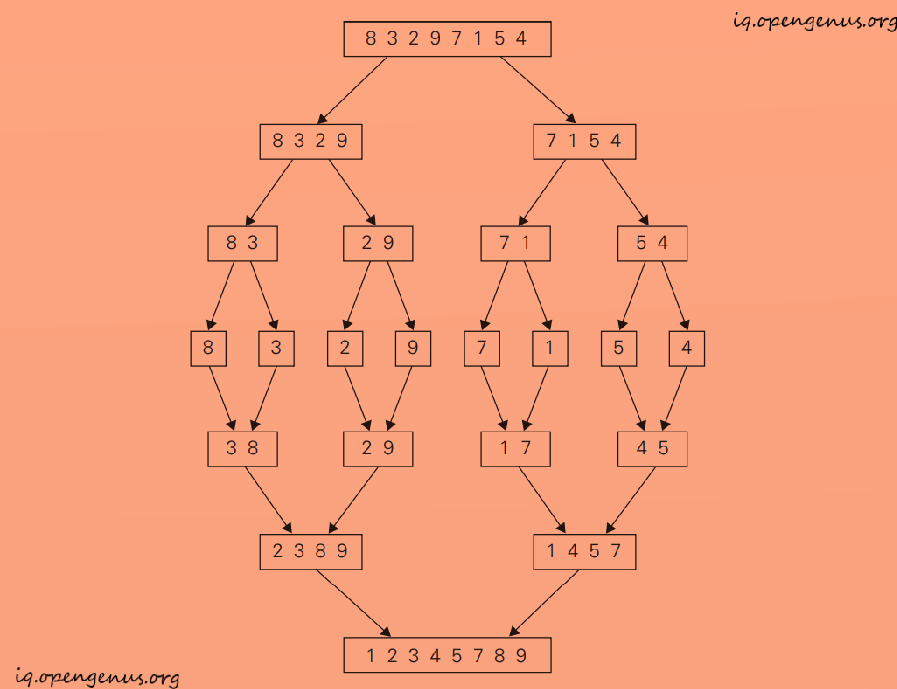
Algorithm for merge sort

ALGORITHM Mergesort(A[0..n − 1])
//Sorts array A[0..n − 1] by recursive mergesort
//Input: An array A[0..n − 1] of orderable elements
//Output: Array A[0..n − 1] sorted in nondecreasing order
if n > 1
    copy A[0..n/2 − 1] to B[0..n/2 − 1]
    copy A[n/2..n − 1] to C[0..n/2 − 1]
    Mergesort(B[0..n/2 − 1])
    Mergesort(C[0..n/2 − 1])
    Merge(B, C, A)

ALGORITHM Merge(B[0..p − 1], C[0..q − 1], A[0..p + q − 1])
//Merges two sorted arrays into one sorted array
//Input: Arrays B[0..p − 1] and C[0..q − 1] both sorted
//Output: Sorted array A[0..p + q − 1] of the elements of B and C
i ← 0; j ← 0; k ← 0
while i<p and j<q do
    if B[i] ≤ C[j ]
        A[k]← B[i]; i ← i + 1
    else 
        A[k]← C[j ]; j ← j + 1
    k ← k + 1
if i = p
    copy C[j..q − 1] to A[k..p + q − 1]
else copy B[i..p − 1] to A[k..p + q − 1]

Quick Analysis

• C(n) = 2C(n/2) + Cmerge(n)
• Cworst(n) = 2Cworst(n/2) + n − 1 from master theorem we can derive that
  Cworst(n) = n log2 n − n + 1.
• Best, average and worst case time complexity: nlogn which is independent of distribution of data.

When to use merge sort?

• Merge sort is used when the data structure doesn't support random access since it works with pure sequential access that is forward iterators, rather than random access iterators.
• It is widely used for external sorting, where random access can be very, very expensive compared to sequential access.
• It is used where it is known that the data is similar data.
• Merge sort is fast in the case of a linked list because need for random access in linked list is low.

Quick Sort

Quick sort algorithm is also based on Divide and Conquer algorithm. It picks an element as pivot(first,last median or random element) and partitions the given list around the picked pivot.
After partitioning the list on the basis of the pivot element, the Quick is again applied recursively to two subarrays i.e., subarray to the left of the pivot element and subarray to the right of the pivot element.

Let's understand with an example :

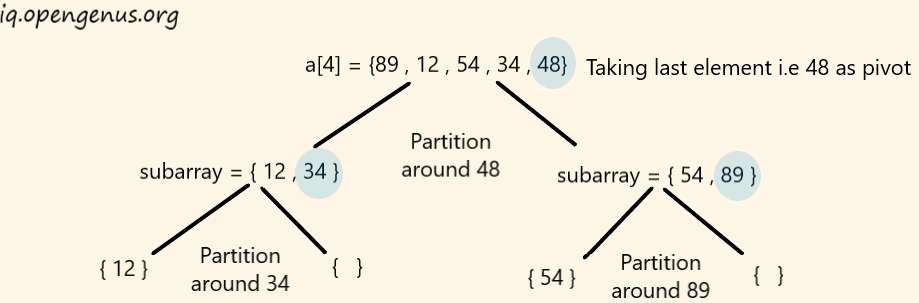
Algorithm for quick sort

ALGORITHM Quicksort(A[l..r])
//Sorts a subarray by quicksort
//Input: Subarray of array A[0..n − 1], defined by its left and right
// indices l and r
//Output: Subarray A[l..r] sorted in nondecreasing order
if l<r
    s ←Partition(A[l..r]) //s is a split position
    Quicksort(A[l..s − 1])
    Quicksort(A[s + 1..r])

Quick Analysis

• Best case and Average case
  T(n) = 2T(n/2) + cn and Cbest(n) = 2Cbest(n/2) + n
  from master's theorem Cbest(n) = n log2 n.
• Worst case analysis
  T(n) = T(0) + T(n-1) + cn
  solving will giveT(n) = O(n^2)

When to use quick sort?

• Quick sort is fastest, but it is not always O(Nlog N), as it becomes O(N^2) in worst cases.
• Quicksort is probably more effective for datasets that fit in memory. For larger data sets it proves to be inefficient so algorithms like merge sort are preferred in that case.
• Quick Sort in is an in-place sort (i.e. it doesn't require any extra storage) so it is appropriate to use it for collections like arrays.

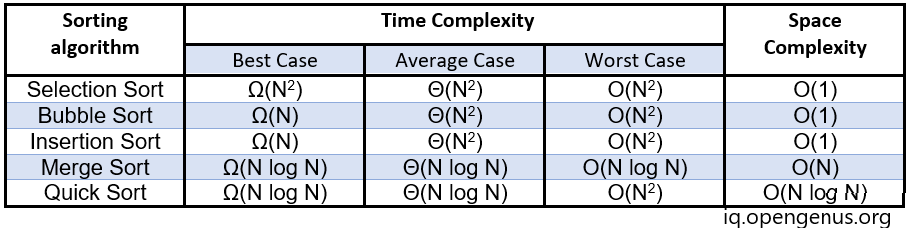
Overall Summary

The table below compares Time and Space Complexity of basic sorting algorithms.

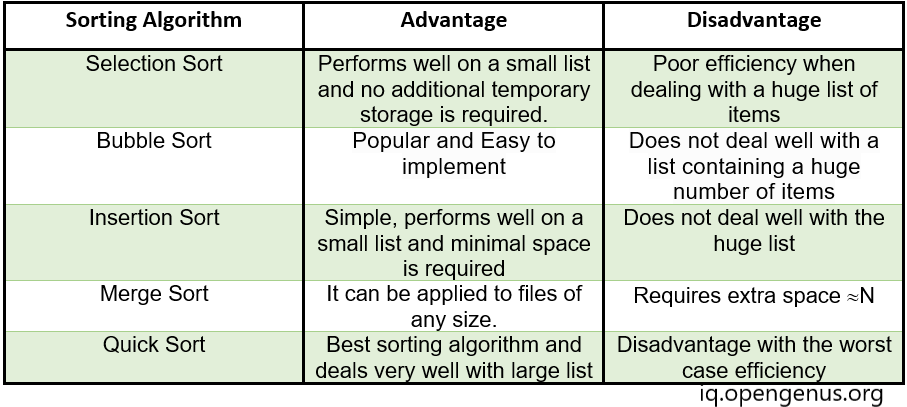
Let's take a look at the some of the advantages and disadvantages of sorting algorithms that we have discussed in this article

Hope this helped you in your journey.

Best wishes for your interview. Crack it like a pro!