In this article, we have explored efficient approaches to find Number of integers between 1 and N that are coprime to N. We have presented the idea of Euler φ (phi) function and is an important topic to get hold on Mathematical Algorithms.

Table of contents:

1. Problem Statement: Co-Prime Numbers
2. Prime-Factors and Sieve Approach
3. Using Euler φ (phi) function (3 algorithms)
   • Method-1 Naive GCD approach
   • Method 2: An extension of Sieve of Eratosthenes
   • Method 3: Euler's Product Formula
4. Applications of Co-prime numbers

Let us get started with Number of integers between 1 and N that are coprime to N.

Problem Statement: Co-Prime Numbers

Two numbers are co-prime if their greatest common divisor is 1.
In other words two numbers are co-prime if the only divisor that they have in common is the number 1. Or using our gcd notation, two numbers X and Y are co-prime if gcd(X,Y) = 1.

Examples:

• 42 and 55 are co-prime, since no number other than 1 divides evenly into both 42 and 55.
• 42 and 56 are not co-prime, since 2 divides into 42 and 56 (as do many other numbers).

Let us try to find the number of co-primes of N in the range 1 to N. We will cover 3 approaches- Prime-Factors and Seive Approach and an easier approach using Euler φ (phi) function.

Prime-Factors and Sieve Approach

The Sieve is one of the most efficient ways to find all primes smaller than n when n is smaller than 10 million or so. You can learn more about the most popular seive, Sieve of Eratosthenes . Let us tweak the well known algorithm to get the number of c-primes

Visual Example

Suppose we need to find the number of co-primes of 20 from the range 2 to 19, then
we first find the prime factors of 20 = {1,2,5}. We then create an array of size 20 and initialize all values to 1. Let us represent the array pictorially.

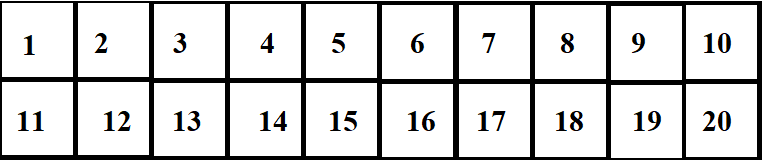
We then take each prime factor of 20 expect 1 and traverse the array making multiples of that prime factor equal to 0.

Let us do it for prime-factor 2

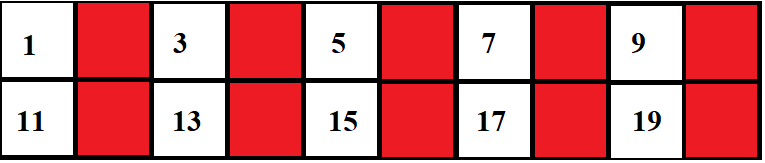
Let us do it for prime-factor 5

The remaining numbers are co-primes of 20

We then initialize counter =0 and traverse the array. If the value of that element is 1, we increment counter.
After traversal we print counter as the answer.

Psuedocode

PRIME FACTORS
find prime-factors of N
For i =2 to N/2
    IF N%i= 0 THEN
        isPrime=1
        FOR j=2 to i/2
            IF i%j= 0 THEN
                isPrime=0
                break
        IF isPrime = 1 
            Add i to Prime Factors array  
END PRIME FACTORS

CO-PRIMES
find co-primes of N in the range 1 to N
Initialize counter=0
Create array of size n and initialize all values to 1
For all prime-factors a : from 2 to n-1
     IF a is 1 THEN
         For all multiples of a (a < n)
             mark multiples of a as 0
For all numbers a : from 1 to n-1
    IF a is 1 THEN
        increment counter
Print Counter
END CO-PRIMES

Code

Let us look at an implementation in C

#include<stdio.h>

int main()
{
    
  	int i, j,n, isPrime; 
  	printf("Enter N: ");
    scanf("%d",&n);
    int arr[n+1], temp=0, coprime_counter=1;
    arr[0]=0;
    
	//initialing all numbers to 1
	for(i = 1; i <= n; i++)
	{
		
		arr[i]=1;
	}
	
  	for (i = 2; i <= n/2; i++)
   	{
     	if(n % i == 0)
        {
   			isPrime = 1;
			for (j = 2; j <= i/2; j++)
			{
				if(i % j == 0)
				{
					isPrime = 0;
					break;
				}
			} 
			if(isPrime == 1)
			{
			    //Seive
				for(int k=i;k<=n;k+=i){
				    arr[k]=0;
				}
			}	          	
		}
   }
   
    
	for(int i=2; i<= n; i++)
	{
		if(arr[i]==1)
		{
		    coprime_counter++;
		}
	}

	printf("The number of coprimes of %d in the range (1,%d) is %d",n,n,coprime_counter);
	return 0;
	
}

For Input: 20

Output: The number of co-primes of 20 in the range (1,20) is 8

The values we counted where {1,3,7,9,11,13,17,19}

Time & Space Complexity

• Worst case time complexity: Θ((n^2)*log(n))
• Average case time complexity: Θ((n^2)*log(n))
• Best case time complexity: Θ((n^2)*log(logn))
• Space complexity: Θ(n)

Using Euler φ (phi) function (3 algorithms)

An approach which is more efficient than the previous one is the GCD or naiave approach. This approach involves checking if the gcd of N and each number in the range 1 to N is 1. In other words, we check if gcd (k,N) = 1, where k=i to N-1.

An easier way to do this would be to use Euler’s Totient function Φ (n) which for an input n is the count of numbers in {1, 2, 3, …, n} that are relatively prime to n, i.e., the numbers whose GCD (Greatest Common Divisor) with n is 1. In other words, the number Φ(n) gives the number of co-primes of N in the range (1,N)

There are three ways to implement Euler φ (phi) function:

• Method-1 Naive GCD approach
• Method 2: An extension of Sieve of Eratosthenes
• Method 3: Euler's Product Formula

They are described below.

Method-1 Naive GCD approach

A simple solution is to iterate through all numbers from 1 to n-1 and count numbers with gcd with n as 1. Below is the visual example of the simple method to compute Euler’s Totient function for an input integer n.

Visual example

Let us find the number of co-primes(φ) of N in the range 1 to N. Suppose N=15,

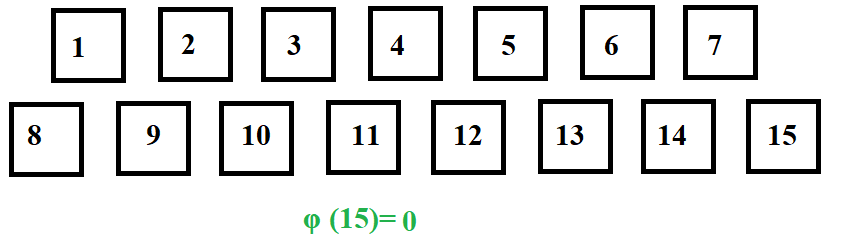
Let us traverse the array and find the GCD of N and the number being pointed to.

GCD(1,15)=1. So φ is incremented.

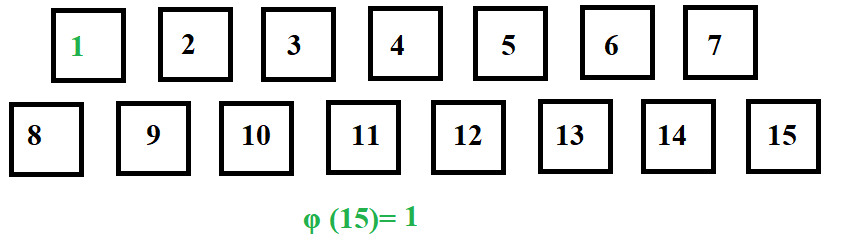
GCD(2,15)=1. So φ is incremented.

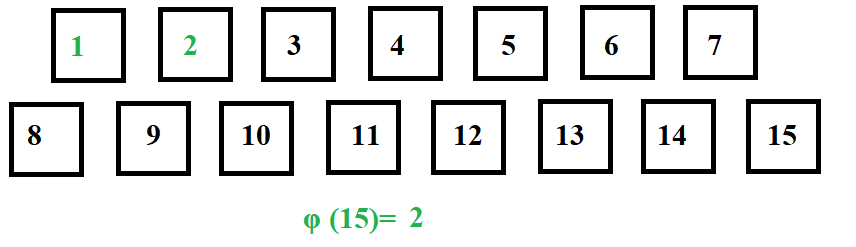
GCD(3,15)=3. So φ is not incremented.

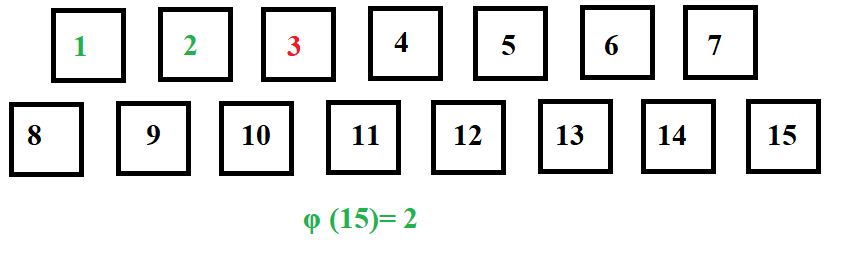
GCD(4,15)=1. So φ is incremented.

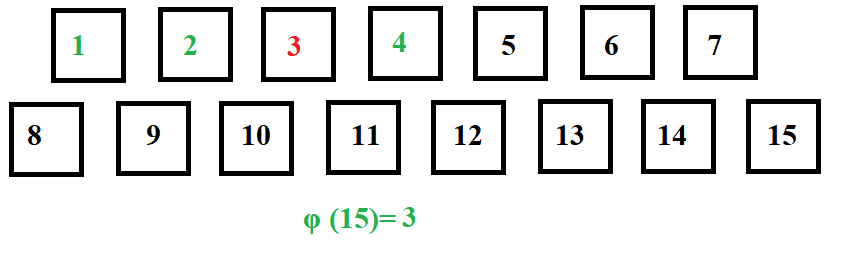
Similarly traversing from 5 to 14, we get:

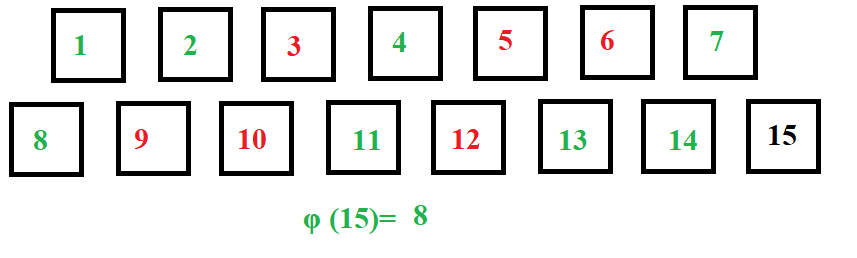
Pseudocode:

BEGIN
FUNCTION GCD (INTEGER n, INTEGER k)
BEGIN
     IF N=0 THEN
         RETURN 0
     ELSE
         RETURN GCD (K%N,N)
END FUNCTION GCD

BEGIN MAIN
INTEGER n   
OUTPUT "Enter Number N:"
INPUT n 
INTEGER INPUT ARR[N+1]
INTEGER φ=0
ARR[0]=0
 FOR  i = 1; i <=n ; i++  THEN    
	FIND GCD OF (n,i)
    IF GCD = 1
        φ++
    END IF
END FOR
 
OUTPUT " THE NUMBER OF COPRIMES OF"+N" IS "+ φ 
END MAIN
END

CODE:

Let us check the C program for the implementation

#include <stdio.h>

int gcd(int n, int k)
{
    if (n == 0)
        return k;
    return gcd(k % n, n);
}


int main()
{

    int n;
    printf("Enter N ");
    scanf("%d",&n);
    int arr[n+1], temp=0, phi=0;
    arr[0]=0;
    
    for (int i=1;i<=n;i++){
        temp=gcd(n,i);
        if(temp==1){
            phi++;
        }
    }
    printf("\nThe number of coprimes of %d in the range (1,%d) is %d",n,n,phi);    
    return 0;
}

For Input: 20
Output: The number of co-primes of 20 in the range (1,20) is 8

The values we counted where {1,3,7,9,11,13,17,19}

Complexity

• Worst case time complexity: Θ(nlogn)
• Average case time complexity: Θ(nlogn)
• Best case time complexity: Θ(nlogn)
• Space complexity: Θ(n)

Method 2: An extension of Sieve of Eratosthenes

If we need all all the totient of all numbers between 1 and n, then factorizing all n numbers is not efficient. We can use the same idea as the Sieve of Eratosthenes. It is still based on the property shown in the second method, but instead of updating the temporary result for each prime factor for each number, we find all prime numbers and for each one update the temporary results of all numbers that are divisible by that prime number.

Algorithm

* Initialize : phi[n+1] phi[0]=0 and phi[1]=1
* Run a loop from 'p' = 2 to n, do the following for every 'p'.
    phi[p]=p
* Run a loop from 'p' = 2 to n, do the following for every 'p'
      If phi[i]=i then 
           Run a loop from 'm' = p to n, do the following for every 'm'
               phi[m]=phi[m]-phi[m]/p
* Return phi[n] 

CODE:

#include <stdio.h>

int phi_1_to_n(int n) {
    int phi[n + 1];
    phi[0] = 0;
    phi[1] = 1;
    for (int i = 2; i <= n; i++)
        phi[i] = i;

    for (int i = 2; i <= n; i++) {
        if (phi[i] == i) {
            for (int j = i; j <= n; j += i)
                phi[j] -= phi[j] / i;
        }
    }
    return phi[n];
    
}


int main()
{

    int n;
    printf("Enter N ");
    scanf("%d",&n);
    
    printf("\nThe number of coprimes of %d in the range (1,%d) is %d",n,n,phi_1_to_n(n));    
    return 0;
} 

For Input: 20
Output: The number of co-primes of 20 in the range (1,20) is 8

Complexity

• Worst case time complexity: Θ(nlong(n))
• Average case time complexity: Θ(nlog(log(n)))
• Best case time complexity: Θ(nlog(log(n)))
• Space complexity: Θ(n)

Method 3: Euler's Product Formula

Below is a Better Solution. The idea is based on Euler’s product formula which states that the value of totient functions is below the product overall prime factors p of n.

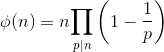
Algorithm

* Initialize : result = n
* Run a loop from 'p' = 2 to sqrt(n), do the following for every 'p'.
      If n%p==0, then 
          Set: result = result - result/p
               n=n/p
          Divide all occurrences of p in n.
*   If n>1 then  
      result = result - result/p
* Return result 

Let us take an example to understand the algorithm:

Visual example

Let us consider N=20. Square of 4 =16<20. Hence we will traverse the array from 1 to 2 to 4 (marked in red)

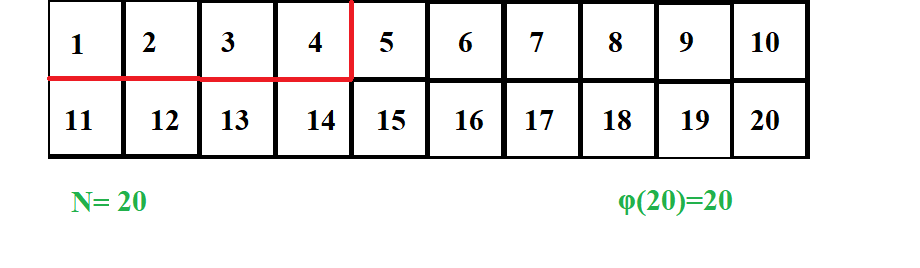
Let us start with 2

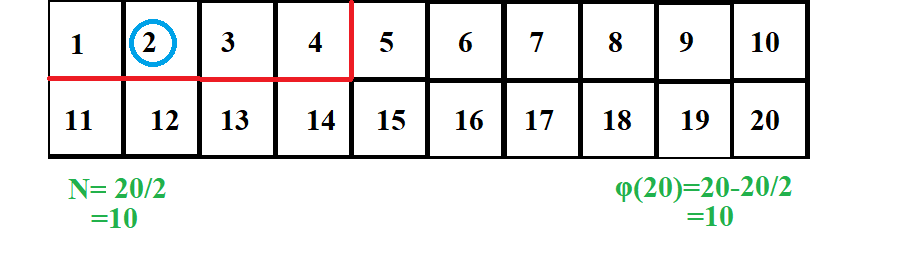
Now N=5. 2 * 2 = 4<5. Hence, We will stop the traversal

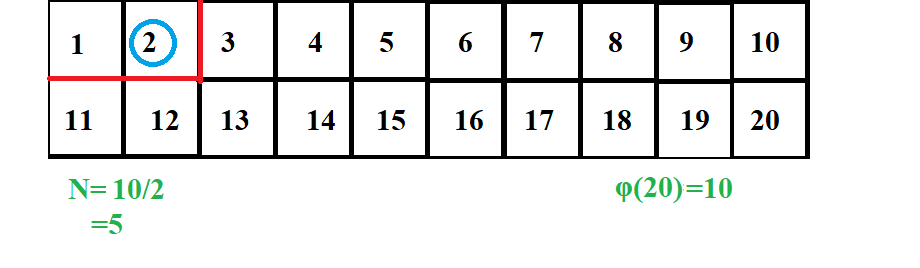
N=5 > 1. Hence, we will now perform the following operations. This is our final answer

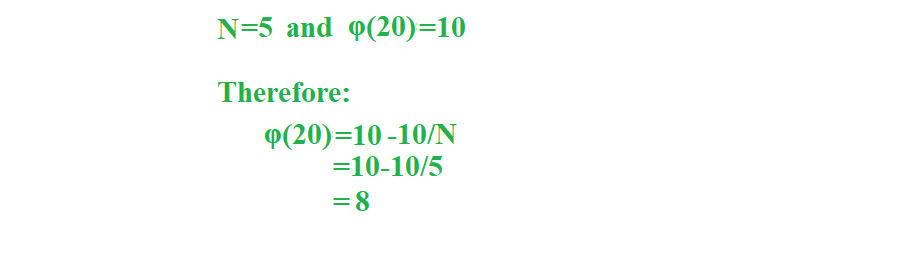
Let us see an implementation of the algorithm in C language

CODE:

#include <stdio.h>

int phi(int n) {
    int result = n;
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            
            while (n % i == 0)
                n /= i;
            result -= result / i;
        }
    }
     
    if (n > 1)
        result -= result / n;
    return result;
}


int main()
{

    int n;
    printf("Enter N ");
    scanf("%d",&n);
    
    printf("\nThe number of coprimes of %d in the range (1,%d) is %d",n,n,phi(n));    
    return 0;
} 

For Input: 20
Output: The number of co-primes of 20 in the range (1,20) is 8

Complexity

• Worst case time complexity: Θ(sqrt(n))
• Average case time complexity: Θ(sqrt(n))
• Best case time complexity: Θ(sqrt(n))
• Space complexity: Θ(log(n))

Applications of Co-prime numbers

• While designing a machine, a smooth and even working is achieved by choosing the tooth counts of the two gears meshing together to be co-prime.* Many rotor machines combine rotors of different numbers of teeth. Such combinations work best when the entire set of lengths are pairwise co-prime.

• In pre-computer cryptography, some Vernam cipher machines combined several loops of key tape of different lengths which are co-primes

With this article at OpenGenus, you must have the complete idea of finding the Number of integers between 1 and N that are coprime to N.