In this post, we discuss the heap data structure and how to create a min and max heap from N given integers in form of an Array. Similarly, inserting elements one by one take O(N logN) time but the optimal approach takes O(N) time.

Table of contents:

1. Introduction to Heap
2. Building a Heap from Array
3. Time Complexity Analysis
4. Applications and problems solved with heaps

Prerequisites:

• Heap data structure
• Heap Sort

Introduction to Heap

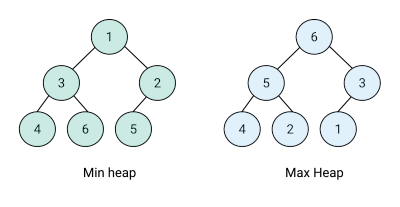
A heap is a binary tree that satisfies the heap property.
The heap property is either a min-heap property or max-heap property.
That is, if B is a child node of A, then key(A) >= key(B) which implies that an element with the greatest key is always the root node, this is called a max heap.
A min-heap on the other hand is such that the root node value is less than or equal to its children.

In a min or max heap, the min or max priority element is always stored at the root of the tree which means a constant time complexity for getMax() or getMin() operations, this is especially useful for solving various problems as we shall see.

Building a Heap from Array

Given an array of size n. We are to build a heap.

Note
For any given node, there are 3 properties to keep in mind.

1. Parent node is $\frac{\mathrm{index}}{2}$.
2. Left child is $(2\times \mathrm{index})+1$.
3. Right child is $(2\times \mathrm{index})+2$.

Steps. (building a max heap)

1. We assign the value of n to variable size(size of heap).
2. For each i from $\frac{\mathrm{n}}{2}$ to 1, sift down the ith element.

Pseudocode

BuildHeap(arr[1...n])
    size <- n
    for i from floor(n/2) down to 1:
        SiftDown(i)

We check for violations of the heap property from bottom of the tree to top.
The inductive base case (ie, depth 0) at the leaf nodes satisfy the heap property, that is, the leaves have no children so naturally the heap property is satisfied.
We start correcting heap violations in all subtrees rooted at depth 1.
Finally when we arrive at the root of the tree, the heap property would have been satisfied for the whole tree.

Sifting down involves moving a node element down the tree to its rightful position until the heap property is satisfied in while sifting up is moving an element up the tree, this is used when inserting into heap/priority queue, we insert at the leaf nodes and bubble up the node to its rightful position in the tree if the heap property is violated.

Steps

1. To select the direction of sifting, we compute the index of left child and right child.
2. If the element is smaller than both or one of its children we select the largest one.
3. If the i is not the largest among its children, we swap it with one of its children.
4. We call Sift down on the swapped element until the max-heap property is satisfied.

Pseudocode

SiftDown(i)
    maxIndex <- i
    l <- LeftChild(i)
    if l <= size and H[l] > H[maxIndex]:
        maxIndex <- l
    r <- RightChild(i)
    if r <= size and H[r] > h[maxIndex]:
        maxIndex <- r
    if i != maxIndex:
        swap H[i] and H[maxIndex]
    SiftDown(maxIndex)

Code

Array Input: [13, 29, 18, 14, 11, 18, 42, 7, 12]

Building max heap

// MAX HEAP
void siftDownMaxHeap(int arr[], int i, int n){
    // parent
    int max = i;
    // left child
    int l = 2 * i + 1;
    // right child
    int r = 2 * i + 2;

    // left child larger than root
    if(l <= n && arr[l] > arr[max])
        max = l;

    // right child larger than root
    if(r < n && arr[r] > arr[max])
        max = r;

    // neither left or right larger
    if(i != max){
        swap(arr[i], arr[max]);
        //recursively siftdown in affected subtree
        siftDownMaxHeap(arr, max, n);
    }
}

void buildMaxHeap(int arr[], int n){
    int start = (n/2) - 1;
    for(int i = start; i >= 0; i--)
        siftDownMaxHeap(arr, i, n);
}

Output

42 29 18 14 11 13 18 7 12

Building min heap

void siftDownMinHeap(int arr[], int i, int n){
    int min = i;
    int l = 2 * i + 1;
    int r = 2 * i + 2;

    // left child smaller than parent
    if(l < n && arr[l] < arr[min])
        min = l;

    //right child smaller tha parent
    if(r < n && arr[r] < arr[min])
        min = r;

    // neither is smal enough
    if(min != i){
        swap(arr[i], arr[min]);
        // recursively siftDown affected subtree
        siftDownMinHeap(arr, min, n);
    }
}
void buildMinHeap(int arr[], int n){
    for(int i = n; i >= 0; i--)
        siftDownMinHeap(arr, i, n);
}

Output

7 11 18 12 13 18 42 14 29 

Time Complexity Analysis

Let's assume we have a complete tree(bottom level is completely full) therefore each level will have $2^{\mathrm{h}}$ nodes.
At the last level there are $2^{\mathrm{h}}$ nodes but we don't call siftDown() for these leaf nodes because they already satisfy the heap property, work done is 0.

At the second to last level there are $2^{\mathrm{h}-1}$ nodes and each might sift down 1 level.

At the third to last level there are $2^{\mathrm{h}-2}$ nodes and each might sift down 2 levels and so on.

Generally, at level j from the bottom there are $2^{\mathrm{h}-\mathrm{j}}$ nodes and each might sift down j levels.

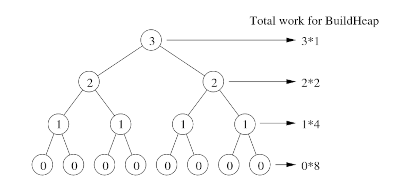
Counting from bottom to top level by level, total time is proportional to
$\mathrm{T}\left(\mathrm{n}\right)=\sum _{\mathrm{j}=0}^{\mathrm{h}}j{2}^{\mathrm{h}-\mathrm{j}}=\sum _{\mathrm{j}=0}^{\mathrm{h}}j\frac{2^{\mathrm{h}}}{2^{\mathrm{j}}}$

Factoring out $2^{\mathrm{h}}$ we have,

$\mathrm{T}\left(\mathrm{n}\right)=2^{\mathrm{h}}\sum _{\mathrm{j}=0}^{\mathrm{h}}j\frac{\mathrm{j}}{2^{\mathrm{j}}}$

We write the infinite general geometric series for any constant x < 1.

$\sum _{\mathrm{j}=0}^{\infty }{\mathrm{x}}^j =\frac{1}{1-x}$

Take the derivative of both sides with respect to x and multiply by x, we have,

$\sum _{\mathrm{j}=0}^{\infty }{\mathrm{jx}}^{\mathrm{j}-1} =\frac{1}{{\left(1-\mathrm{x}\right)}^2} \sum _{\mathrm{j}=0}^{\infty }{\mathrm{jx}}^{\mathrm{j}} =\frac{\mathrm{x}}{{\left(1-\mathrm{x}\right)}^2}$

We plug x = 1/2 to the initial sum and we have the desired formula;

$\sum _{\mathrm{j}=0}^{\mathit{\infty }}\frac{\mathrm{j}}{2^{\mathrm{j}}}=\frac{1/2}{(1-(1/2){)}^2}=\frac{1/2}{1/4}=2$

This is a bounded sum which we shall use for approximating the time complexity.

$\mathrm{T}\left(\mathrm{n}\right)=2^{\mathrm{h}} \sum _{\mathrm{j}=0}^{\mathrm{h}}\frac{\mathrm{j}}{2^{\mathrm{j}}}\le 2^{\mathrm{h}} \sum _{\mathrm{j}=0}^{\mathit{\infty }}\frac{\mathrm{j}}{2^{\mathrm{j}}}\le 2^{\mathrm{h}}·2=2^{\mathrm{h}+1}$

Recall, n = $2^{\mathrm{h}+1}-1$ therefore we have $\mathrm{T}\left(\mathrm{n}\right)\le \mathrm{n}+1\in \mathrm{O}\left(\mathrm{n}\right)$ -the algorithm accesses every element of the array at least once.

Therefore total running time is $\mathrm{\Theta }\left(\mathrm{n}\right)$.

Applications and problems solved with heaps

1. Heaps are used to implement priority queues. Priority queues are useful in numerous occasions such as task scheduling in operating systems where tasks are have priorities, that is the topmost root node represents the highest priority task therefore it will be processed first.

2. Heap sort - a fast and space efficient(in-place) sorting algorithm with O(nlogn) in the worst case. Here we create an empty priority queue then insert the elements into the priority queue then extract the maximum one by one placing it in the last position of sorted array.

3. Last k elements of a sorted array.
   Input: An array arr[1...n] and an integer k
   Output: The last k elements of a sorted version of arr.
   We use heaps to solve this in linear time O(n) when $k \le O\left(\frac{n}{\log n}\right)!$
   To solve this, we build a heap and extract the max value k times.
   The time complexity is O(n + klogn), it takes linear time for building heap and klogn time for extracting max.
   We can also extend this to finding the kth largest element.

4. Huffman coding compression algorithm is a data compression algorithm, we use priority queues for building the Huffman Tree whereby the node with the lowest frequency has the highest priority.

5. Introsort sorting algorithm, this is an in-place sorting algorithm. It is a hybrid of both heap sort and quick sort and this makes it better than all other sorting algorithms. It uses quick sort at the start of the algorithm and then switches to heap sort when the recursion depth exceeds a level based on elements being sorted.

References

min heap visualization
priority queues
heap sort

Questions

Find the first k non-repeating characters in a string in a single traversal using heaps.

With this article at OpenGenus, you must have the complete idea of how to Create a Heap from Array of N integers.