Delaunay Triangulation

In this article, we discuss Delaunay Triangulation, its relation to Voronoi diagrams and algorithms to compute Delaunay Triangulation. This is an important topic in Computational Geometry.

Table of contents:

1. Motivation of Delaunay Triangulation
2. Height interpolation
3. Delaunay Triangulation
   • Delaunay graph
   • Properties of Delaunay Graph
   • Characterization
   • Angle Optimal Triangulations
4. Complexity of a triangulation
5. How to choose a good triangulation?
6. Edge flips
7. How to determine illegal edges without comparing angles
8. Legal triangulations
9. Computing Delaunay Triangulation (Randomized incremental construction using edge flips)
10. Conclusion

Prerequisite: Voronoi diagrams

Motivation of Delaunay Triangulation

We want to estimate rainfall and come up with a precipitation map for a country, data is not always available because rain gauge networks are not evenly distributed therefore we use spatial interpolation to estimate rainfall at locations without recorded data by using known rainfall readings at nearby locations.

Spatial interpolation, this is a process of using points with known values to estimate the values of other unknown points.

We shall discuss height interpolation to explain spatial interpolation.

Height interpolation

Problem: We are given a topographical map.

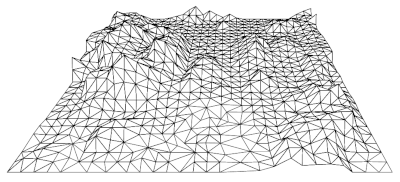
We want to measure and show heights of all points from absolute 0.
Naively, we can measure all heights from every point on the map but this will be cumbersome.
Optimally, we can take the heights of some points and interpolate the rest of the points, that is use the known to get the unknown. This is called height interpolation.
To do this we fly a plane over a map and we get the height measurements for different points on the map p = (px, py, pz).

We project the points on the plane and get a map.

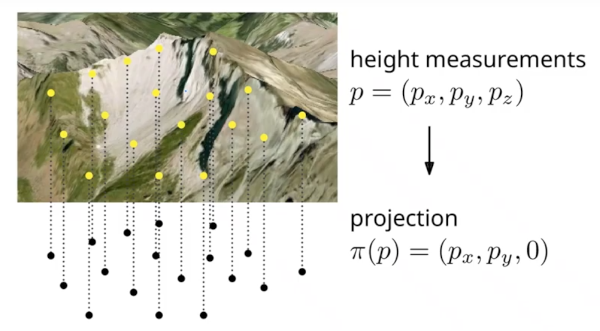
Therefore to estimate the height of other closer points (x, y). We interpolate by looking at few closer points.
To interpolate we use triangulation of the point set.

How?

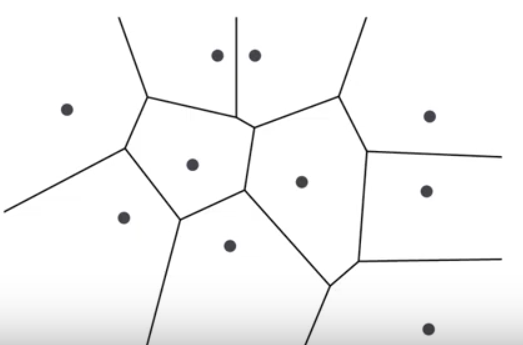
We subdivide the plane into cells such that within each cell every point has the same nearest neighbor from any point in the cell, this is called a voronoi diagram, We have also discussed voronoi diagrams here.

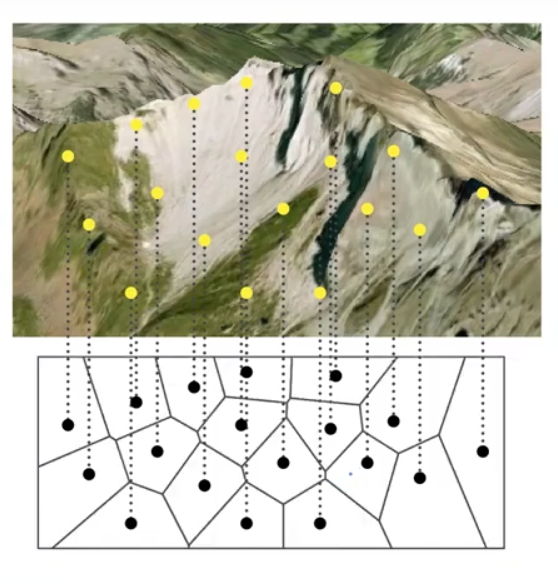
Given two heights, we can interpolate between the heights easily to get an unknown, given a plane with multiple points(heights), we need to choose heights which we then use to interpolate from a chosen height. This is where triangulation comes in.

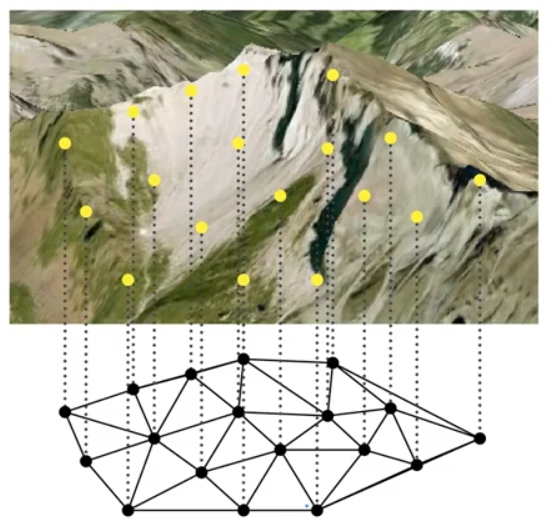
The image above represents a subdivision of a plane into triangles within the convexity of the points.
Now, to get an unknown we take 3 vertices of a triangle and interpolate appropriately.

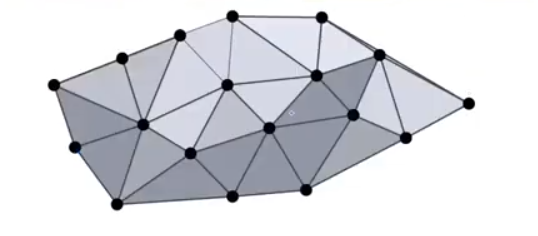
Delaunay Triangulation

Definition: Given $\mathrm{P}\subset {\mathbb{R}}^2$, a triangulation of P is a maximal planar subdivision with vertex set P.

A triangulation can also be defined as delaunay if for every triangle it holds that the interior of its surrounding circle is empty. empty circumcircle property. visualize
We will see this in the properties section.

Delaunay graph

Given a set P of n points on a plane.
Vor(P) = subdivision of the plane into voronoi cells, edges and vertices.

Dual graph: The graph G = (P, E) with E = {(p,q) | V(p) and V(q) are adjacent} is called the dual graph of Vor(P).
The delaunay graph is the dual graph of the voronoi diagram.
That means, for every cell of the voronoi diagram, we want to have a vertex in the delaunay graph.

We add edges between two points if the points are adjacent(share an edge) to each other in the voronoi diagram to get a dual graph.

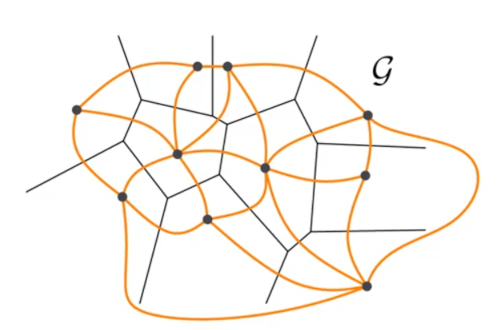
We straighten the lines of the dual graph to obtain a delanuay graph.

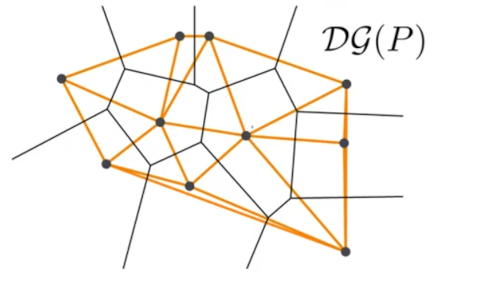
Definition: The delanuay graph DG(P) is the straight line drawing of graph G.

Properties of Delaunay Graph

Planarity. (no crossings)
Lemma: $\mathrm{P}\subset {\mathbb{R}}^2$ finite $\Rightarrow$ DG(P) plane.

proof: (by contradiction).
Edge pq is in $\mathrm{DG}\left(\mathrm{P}\right)\iff \exists {\mathrm{D}}_{\mathrm{pq}}$ closed disk such that $\mathrm{p},\mathrm{q}\in \partial {\mathrm{D}}_{\mathrm{pq}}$ and $\{p,q]={\mathrm{D}}_{\mathrm{pq}}\cap P$
A property of voronoi edges, if we have two cells that correspond to two sides p and q, then we have an edge p and q in the delanuay graph iff there is an edge between the cells in the voronoi diagram.

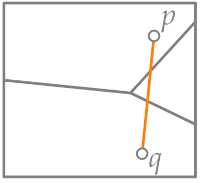
We have a voronoi edge iff there is a closed disk that contains the two sides on its boundary and no other points in its boundary or interior.

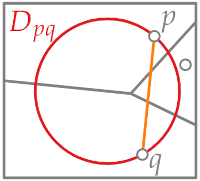
Let say C is the center of the disk and we have the two edges spq and sqp between p and the center and between q and the center.

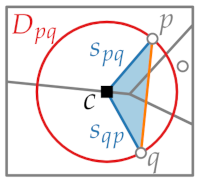
We assume that there is a crossing that is, any other edge in the delanuay graph uv that crosses the edge pq.

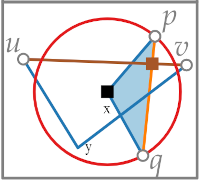
We obtain two triangles pqx and uvy.

Since there is an edge, there has to be a disk that contains uv on its boundary and no other point on its boundary or interior.

u and v cannot lie in the disk of p and q because of the $t_{pq}$ edge, therefore uv cannot lie inside the triangle pqx, the only way a crossing exists between uv and pq, is that the edge $t_{pq}$ crosses another point(z) of the triangle.

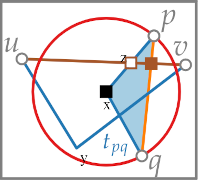
We have 2 triangles that intersect at exactly 3 points, but they have to intersect in an even number of points.
pq has 2 intersections, uv has 2 intersections. The remaining intersection involves the blue edges.

The blue edges are defined by a site and the center of the circle which lies in the voronoi edge, therefore the edge spq has to go from one voronoi cell to its boundary.
sqp lies in the cell q and spq lies in the cell p,
suv lies in cell u and svu in cell v.
This means they can only intersect at their end points.
Therefore they have to intersect in the center so that both disks have the same center therefore none of them can be empty.

$S_{pq}\subset V\left(p\right),S_{pq}\subset V\left(q\right),S_{uv}\subset V\left(u\right),S_{vu}\subset V\left(v\right)$

This means that all vertices have to lie in the same circle, which is not possible, and we have contradiction.
We cannot have a crossing between pq and uv, therefore the graph is plane.

Characterization

Given a finite point set $\mathrm{P}\subset {\mathbb{R}}^2$.
(i) Three points $p,q,r\in P$ are vertices of the same face in the delanuay graph iff there is a voronoi vertex.

That is, there is some disk that contains the 3 points on its boundary but no other points in its interior.
$DG\left(P\right)\iff interior\left(C\right(p,q,r\left)\right)\cap P=\oslash$

(ii) We have an edge iff there is a voronoi edge, that is, a there is a disk that contains exactly the two sides on its boundary and no other sides in the interior.
$\partial \mathrm{D}\cap \mathrm{P}=\{\mathrm{p},\mathrm{q}\} \mathrm{and} \mathrm{interior}\left(\mathrm{D}\right)\cap \mathrm{P}=\oslash$

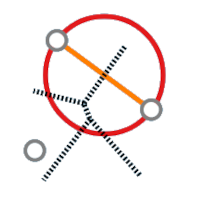
Note: A delanuay triangulation is a triangulation that has a delanuay graph as its subgraph.

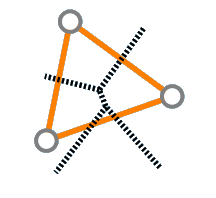
Angle Optimal Triangulations

Definition: A triangulation of a point set $\mathrm{P}\subset {\mathbb{R}}^2$ is a maximal planar subdivision with vertex set p.
Planarity means it is non-crossing as we have shown in the above section.
It is also maximal as we add as many edges as possible so that every face forms a triangle

We observe the following;

• Any inner face is a triangle.
• The outer face is a convex hull(the opposite of the outer face) CH(P).

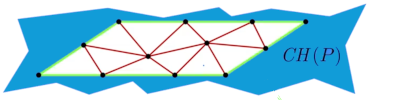
Complexity of a triangulation

Theorem: Let P be a set of n non-collinear points(if they are collinear no triangle can be formed) and let h be the number of vertices of CH(P).
Then every triangulation P has t(n, h) triangles and e(n, h) edges.

To compute t(n, h) and e(n, h), we can use Euler's polyhedron formula for connected planar graphs. That is #faces - #edges + #vertices = 2 including the outer face.

If the convex hull is small enough(3 points) we have 2n -5 triangles and 3n - 6 edges and as the complexity of the convex hull increases the number of edges and triangles decreases.

In general we have 2n -2 - h triangles and 3n - 3 - h edges.

Given a point set we have many ways to triangulate it.
We first used a voronoi diagram where we used height interpolation to estimate unknowns following that we want to use triangulations to obtain a continuous height of the plane.

How to choose a good triangulation?

We are given the following points set with different triangulations.

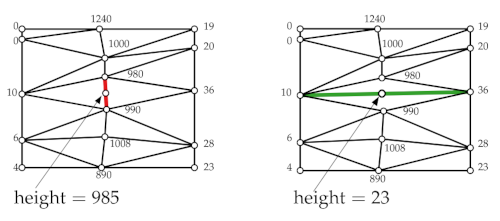
They differ in the green and red points respectively, If we want to perform height interpolations between the two points we obtain 985 and 23 when we interpolate on the red edge and green edge.

It is more probable that 985 is correct since the edge is much shorter, it is also more natural to go with values that are much closer to the points.

That is, on the left image we have a consistent terrain of high points(mountains/hills) but in the second there are high terrains(mountains) and then a sudden drop(valley) which is not consistent.

We could also argue that the second gets its values from points that are far away (thin triangles).
Intuition: We want to avoid thin triangles - this is caused by small angles which means that we want to maximize the smallest angle within a triangle.

Definition(angle vectors): Let T be a triangulation of P with m triangles and 3m vertices. Its angle vector is $\mathrm{A}\left(\mathrm{T}\right)=({\mathrm{\alpha }}_1,...,{\mathrm{\alpha }}_{3\mathrm{m}})$ where ${\mathrm{\alpha }}_1,...,{\mathrm{\alpha }}_{3\mathrm{m}}$ are the angles of T sorted in increasing value.

For the two triangulations $T$ and $T^{\text{'}}$ we define an order A(T) > A($T^{\text{'}}$) according to the lexographical ordering.
That is we look at the smallest angle and sort then based on that value.
The first(left) will be higher than the second because it has a higher starting value.

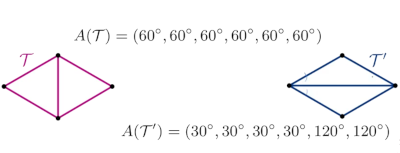
Therefore in terms of angle optimality and avoiding small angles we would choose the first which is maximal.

We state that a triangulation is angle optimal if its angle vector is larger than or equal to any other angle vector of any other triangulation.

Edge flips

Definition: Let T be a triangulation. An edge e of T is illegal if the smallest angle of the triangles incident to e can be increased by 'flipping' e.

Given the edge e below, if we flip it we get a larger angle, therefore we say that e is an illegal edge.

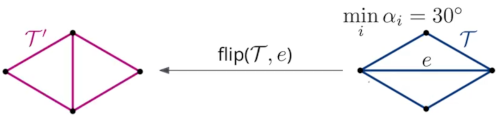
To get an angle optimal triangulation we have to flip the edge e.
Note: Flipping an edge also means that angle vector will have increased in terms of lexical graphical ordering.

How to determine illegal edges without comparing angles

Thales theorem: If line ab is a diameter, then the angle at any third point on the circle C is 90 degrees.
That is, diameter of a circle always subtends a right angle to any point on the circle.

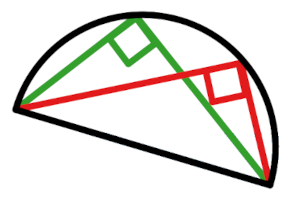
A generalization (Thales++).
Theorem: Let C be a circle, l a line intersecting C in points a and b and p, q, r, s be points lying on the same side as l. Suppose that p, q lie on C, r lies inside C and s lies outside C.
Then $\measuredangle arb>\measuredangle apb=\measuredangle aqb>asb$ where $\measuredangle abc$ denotes the smaller angle defined by 3 points a, b, and c.

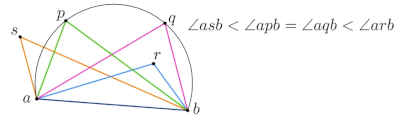
Simply put, angles within the circle at any point are equal, outside angles are smaller than the ones on the circle and inner angles are larger than all angles.

Legal triangulations

We use the generalized theorem to characterize an edge as legal or illegal.

Lemma: Let $△$prq and $△$pqs be two adjacent triangles in T and C be the circumcircle of $△$prq.
Then $\overline{pq}$ is illegal $\iff$ $\mathrm{s}\in \mathrm{interior}\left(\mathrm{C}\right)$

If p, q, r, s form a convex quadrilateral and $\mathrm{s}\notin \partial \mathrm{C}$ then either $\overline{pq}$ or $\overline{rs}$is illegal.

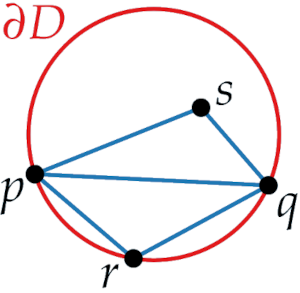
We want to know whether pq is illegal, therefore we look at the incident triangles prq and pqs, which gives us the points r and s.
Then pq is illegal iff we take the circumcircle p q r, and find that s lies inside this circle then pq is illegal but if s lies outside then pq is legal.

Proof.
We want to show that for all angles in the triangulation after the flip, there is an angle in the original triangulation that is smaller.
$\forall {\mathrm{\alpha }}^{\text{'}} \mathrm{in} {\mathrm{T}}^{\text{'}} \exists \mathrm{\alpha } \mathrm{in} \mathrm{T} \mathrm{s}.\mathrm{t} \mathrm{\alpha }<{\mathrm{\alpha }}^{\text{'}}$

We have the new two angles, for both we have smaller angles(colored orange)

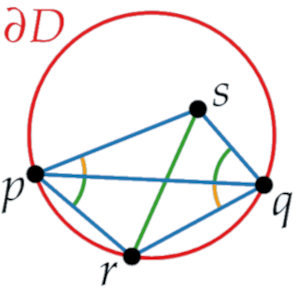
We look at the angle ${\mathrm{\alpha }}^{\text{'}}$ in qrs and we extend the segment rs until we hit the disk.

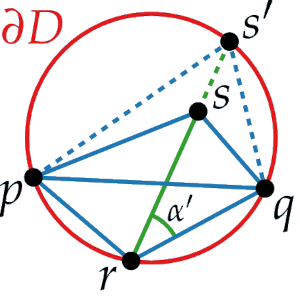
We use the segment between ${\mathrm{S}}^{\text{'}}$ and q as the base segment for thales++ generalized theorem.

According to the theorem, if we consider the angle ${\mathrm{\alpha }}^{\text{'}}$ and the angle at spq, they are exactly the same because they both lie on the circle.

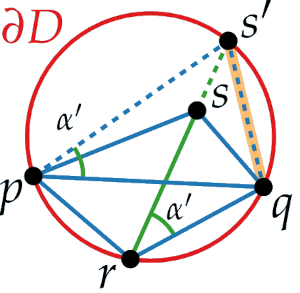
Looking at the angle sqp, for ${\mathrm{\alpha }}^{\text{'}}$ we found a smaller $\mathrm{\alpha }$.
We can do the same for the remaining three angles and find a smaller $\mathrm{\alpha }$ in the blue colored triangulation.

This means that the minimum of blue angles has to be smaller that the minimum of green triangulation.

Is s lies on the boundary of the disk $\mathrm{s}\notin \partial \mathrm{D}$, then both pq and rs are legal. That is, if we take the blue triangulation, the we show that s is not in the interior of the disk so pq is legal and if we take the green triangulation, we show that p is not in the interior of the disk so sr is legal.
This means that there could be more that one legal triangulations, meaning however we flip the edges we end up with a legal triangulation.

Proof that a legal triangulation exists.

Algorithm:

Let T be any triangulation of P.
While T has an illegal edge e, flip e 
Return T.

A(T) increases for every flip and there is a finite number of triangulations of P, (P < ∞) therefore this algorithm will at some point have to terminate after some finite number of steps.

With have shown that every angle-optimal triangulation is legal, if it is illegal we can improve it then it is no longer angle optimal.

Computing Delaunay Triangulation (Randomized incremental construction using edge flips)

We are given the following point sets,

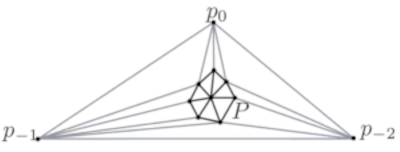
The 3 outer points represent the outer face.

Algorithm:(Delanuay Triangulation)

1. Initialize T as a triangle △p0, p-1, p-2 containing all points form P.
2. Compute a random permutation of p1, ... pn;
3. For r <- 1 to n do the following
4. Insert(${\mathrm{p}}_{\mathrm{r}}$, T)
5. Discard p0, p-1, and p-2 with all their incident edges.
6. Return T.

Explanation.

• Create a larger outer triangle.
• Randomly permute points to use randomized incremental construction.
• We insert the points one by one to the current triangulation creating a delanuay triangulation.
• After the steps we discard the outer triangle. and what remains is the delanuay triangulation of the point set.

Algorithm. INSERT(pr, T)

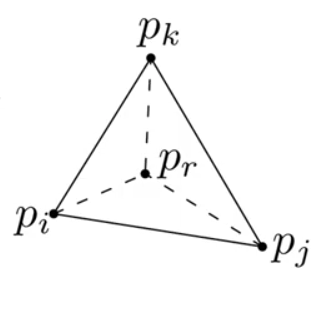
1. Find triangle ∈ T containing ${\mathrm{p}}_{\mathrm{r}}$.
2. If pr lies in △pi pj pk do the following
3. Add edges from pr to pi, pj, pk
4. LegalizeEdge(pr, pi pj, T)
5. LegalizeEdge(pr, pj pk T)
6. LegalizeEdge(pr, pk pi, T)
7. else (pr lies on edge pi pj)
8. LegalizeEdge(pr, pi pl, T)
9. LegalizeEdge(pr, pl pj, T)
10. LegalizeEdge(pr, pj pk, T)
11. LegalizeEdge(pr, pk pi, T)

Explanation.
We check legality of opposing edges pi pk, pk, pj and pi, pj by calling LegalizeEdge recursively three times.
If edge is not legal we flip and check the remaining edges.

Algorithm. Legalize Edge(pr, pipj, T)

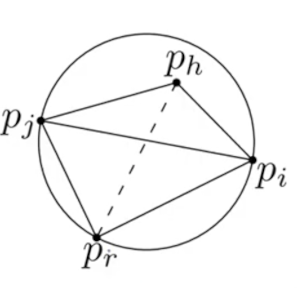
1. If pi pj is illegal then flip edge.
2. Let △pi pj ph be the adjacent triangle.
3. Replace pi pj by pr ph.
4. LegalizeEdge(pr, pj ph, T).
5. LegalizeEdge(pr, ph pi, T).

Explanation
We check whether it is illegal by checking whether the point on the other side in the circumcircle of the triangle pi pj pr.
If it is inside, the edge is illegal so we flip.
Then recursive call the algorithm on the edges pj ph and ph pi.

Conclusion

Theorem:
A delanuay triangulation of an arbitrary set of n points in a plane can be computed in O(nlogn) time.
We compute the voronoi diagram and dual graph and fill holes to get delanuay triangulation.

Colloray:
If the points are in general position, we get an angle optimal triangulation of a set of n points in O(nlogn) time.

Colloary:
If the points are in arbitrary positions we can maximize the minimum angle in O(nlogn) time by filling the holes arbitrarily.

Corollary:
An angle optimal triangulation of an arbitrary set of n points can be computed in O(${\mathrm{n}}^2$) time.
We compute the delanuay graph, and fill holes(vertices on a common circle) to optimize the angle vector for each hole. which are completely independent from each other.
We triangulate and use the flipping algorithm until we get an angle optimal sequence, after ${\mathrm{n}}^2$flips we get an optimal.
Which translates to ${\mathrm{n}}^2$ time for filling these holes.

References

• Notes on Delanuay Triangulation and Height Interpolation by Department of Information and Computing Sciences at Utrecht University
• Two algorithms for constructing a Delaunay Triangulation by D. T. Lee and B. J. Schachter (published in February 1980) at International Journal of Computer and Information Sciences.

With this article at OpenGenus, you must have a strong idea of Delaunay Triangulation.