In this article, we will learn about prime numbers and the twin prime conjecture. We will also look at an efficient algorithm for finding the first twin prime pairs up to a number N.

Table of contents:

1. Introduction to Prime Numbers
2. The Twin Prime Conjecture
3. Finding Twin Primes up to a number N
4. Space and Time Complexity

Let us get started with Finding the twin primes up to N (Twin Prime Conjecture).

Introduction to Prime Numbers

A prime number is a natural number that is only divisible by one and itself, which means it can only be represented as a product of one and itself

Any number that is not prime is known as a composite number, meaning that it can be formed as a product of smaller numbers. For example, 11 is a prime number as it can only be represented as 11 * 1, but 8 is a composite number as it can be represented as 2 * 4 as well as 8 * 1.

Prime Numbers play important roles in computer science. One of the fields where they are used a lot is cryptography.

The Twin Prime Conjecture

A twin Prime Pair is a pair of prime numbers (a,b) such that a is less than or greater than b by 2. In other words, they are prime numbers pairs such that the difference between them is exactly equal to two.

The Twin prime conjecture states that there are infinitely many twin primes. It is called a conjecture because although the statement might be true, it has not yet been proven to be true.

Finding Twin Primes up to a number N

The Algorithm

The steps to find twin primes up to a number N are:

1. Identify the first prime numbers up to N
2. Identify the Twin prime pairs among the identified primes
3. Display result

Step 1

In order to identify the first prime numbers up to N, We shall use an algorithm known as the Sieve of Eratosthenes. It is an algorithm that finds all the prime numbers up to a number N so it is exactly what we are looking for.

The Sieve of Eratosthenes works by first instantiating all the numbers from 2 to N in a list or grid. Starting from two it iteratively marks all the multiples of every prime number it encounters as composite. By the end, all the numbers that have not been marked are exactly the prime numbers up to N.

We can visualise this with an example.

The above grid has 50 numbers which means we want to find the first prime numbers up to 50.

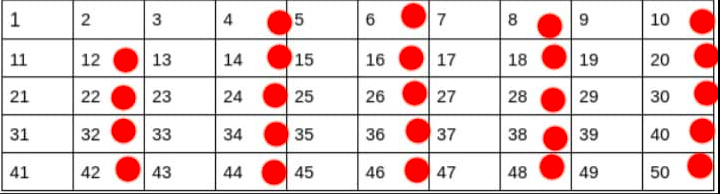
Following the algorithm and starting from two. We mark all the multiples of two in the grid as they are not prime.

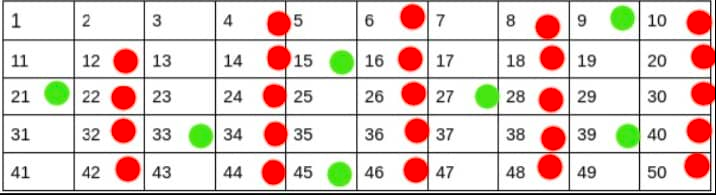
We move to the next unmarked number 3 which we know will be prime, we mark its multiples. There will be overlap but we only have to worry about the multiples not yet marked.

The next unmarked number is 5. We mark the multiples of 5 that haven't yet been marked. You might be noticing a trend, the next prime number always ends up marking a smaller number of multiples because some of its multiples have already been covered by the previous smaller primes.

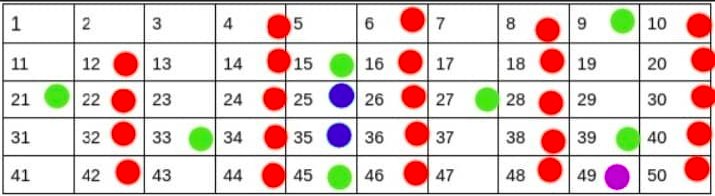
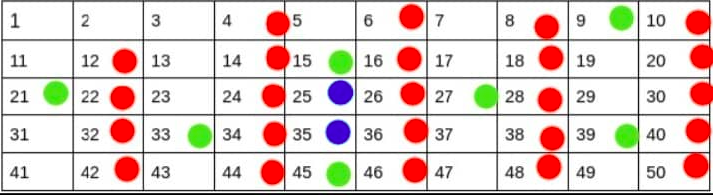
Lastly, we mark the multiples of seven. After this, we can terminate the algorithm. We know that we can terminate because the square of the next unmarked number 11 is 121 which is greater than 50. All the other smaller multiples of 11 would have already been covered by the smaller primes. and since 11 is the smallest unmarked number with a square greater than 50 we can be safe in our decision to terminate.
After termination, we can be assured that all the unmarked numbers are valid prime numbers.

Python Implementation

def findPrimes(N):
    """
    Uses The Sieve of Eratosthenes to find the first prime numbers up to N.
    input: N, a natural number
    returns: A set of the first prime numbers up to N
    """
    # Initialise a boolean array where the index maps to a number up to n
    # All the numbers are first initialised as True
    # Eventually after the sieve is run, isPrime[i] will be False if i is 
    # composite
    isPrime = [True for x in range(N + 1)]
	
    candidate = 2
    # starting from 2 iterate and mark all the multiples
    while candidate ** 2 <= N:
        if isPrime[candidate]:
            for k in range(candidate * 2, n + 1, candidate):
                isPrime[k] = False
        
        candidate += 1
        
    # Use boolean array to filter only the prime numbers to a new List
    onlyprimes = [i for i in range(2, len(isPrime)) if isPrime[i]]	
    
    # Convert to a set for constant lookup operations and return
    return set(onlyprimes)

Step 2

Now we need to be able to identify twin primes. This is actually easy to do. Everything we need is in the definition. We simply have to iterate through the prime numbers and pick out pairs of prime numbers whose difference is 2.

Python Implementation

def findTwinPrimes(primes):
    """
        takes in a set of prime numbers and finds all the twin primes
        input: A set of prime numbers
        returns: A list of twinprime tuples
    """
    twinPrimes = []
    for prime in primes:
        if prime + 2 in primes:
            twinPrimes.append((prime, prime + 2))
   
   return twinPrimes

Step 3

We can tie it all up together and display our results.

def printPrimePairs(n):
    """ 
        Prints out the first prime pairs up to n
    """
    primes = findPrimes(n)
    twinprimes = findTwinPrimes(primes)

    # print results to console
    for pair in twinprimes:
        print(pair)
        

Finally lets Test our method with an actual value

    printPrimePairs(50)
    (3, 5)
    (5, 7)
    (11, 13)
    (17, 19)
    (29, 31)
    (41, 43)

Space and Time Complexity

The Sieve of Eratosthenes has a time complexity of O(n log log n) and space complexity of O(n). FindPrimes which implements it also has the same time and space complexity.

FindTwinPrimes has a time complexity of O(d) where d < n it also has a space complexity of O(d)

PrintPrimePairs which encapsulates both functions will be bounded by the higher time complexity so it has a time complexity O(n log log n) and a space complexity of O(n).

With this article at OpenGenus, you must have the complete idea of finding twin primes up to number N and the Twin Prime Conjecture.