In this article, we have explained the basic of Bubble Sort along with a detailed explanation of Python implementation of Bubble Sort in a list.

Table of contents:

1. Introduction to Bubble Sort
2. Python implementation of Bubble Sort with explanation
3. Complexity and Runtimes
4. Applications of Bubble Sort

Let us get started implementing Bubble sort in a list in Python.

Introduction to Bubble Sort

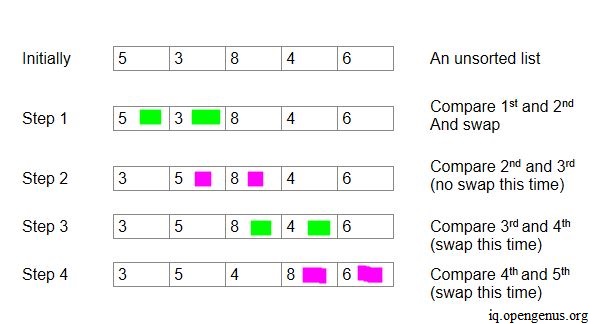
The bubble sort algorithm sorts an unsorted list in the correct order. It involves looking at two adjacent elements of a list and then swapping them in the correct order. This is done till the end of the list and till all elements end up in the correct order. The swapping of elements only occurs when the adjacent elements are in an incorrect order. The bigger numbers bubble up to the right when sorting, hence the name bubble sort.

Syntax and flow

The bubble sort algorithm can be easily implemented using a for-loop. Implementation requires the following steps-

1. Get the length (i.e the number of elements in a list) of the list. Let the number of elements in a list be 'n'.
2. Go through the list 'n' number of times and create a variable to check for any swaps. Traverse through all elements of the list 'n-i-1' times every time. This is because at each iteration, the last element always gets set in the correct order.
3. When traversing through all elements, each time check whether the current element is greater than the next element. If so, swap them.
4. If no swap occurs, break out of the loop.
5. Print the final sorted list.

Python implementation of Bubble Sort with explanation

The following program sorts an unsorted list using a for-loop and prints the final output.

# a function to sort a list using bubble sort algorithm
def bubblesort(lst):
        # get the length of the list
        n = len(lst)
        # go through the list n number of times
        for i in range(n):
                # variable to keep check for any swaps
                swap = False
                # traverse through all adjacent elements
                for j in range(0, n-i-1):
                    # if current element greater than next element, swap them
                    if lst[j]>lst[j+1]:
                        lst[j], lst[j+1] = lst[j+1], lst[j]
                        swap = True
                # if no swaps, then break out of the loop
                if swap == False:
                        break
        # print the final sorted list
        print(lst)

# an example unsorted list 
y = [1,5,4,6,7,8,3,2,12,10,9,11]

# function call to sort list y
bubblesort(y)

1. First, we create a function named 'bubblesort' using the def statement. This statement is used whenever we need to create a custom function for our program in Python. The function name can be anything, but 'bubblesort' makes sense here as the focus is on bubble sort algorithm. To create a function, first type def followed by the preferred name of the function. Then, inside the parenthesis, in function definition, we pass in parameters, which are an alias of the actual variable that we later pass in the function call. Think of parameters as temporary variables that we use inside the function to specify the changes to be performed on the actual variable. Here the parameter is named lst.

2. We then create a variable named 'n' that stores that length of the list (the number of items in a list). To get the length of a list in Python, type len and inside the parenthesis, pass in the name of the list. Here, since it's a function definition, we pass in the temporary variable as before, which is the parameter named lst.

3. After that, we use a for loop that goes through the list 'n' number of times. The value of i ranges from 0 to 'n-1', since the range keyword includes the value upto 'n' but not including 'n'. Hence, for all values of 'i' implies values starting from 0 and upto but not including 'n'.

4. Then we create a variable called swap that stores a boolean value ( i.e true or false). We use this variable later to check whether any swaps happen or not. The initial value is set to False, implying that as of yet, no swap occurs.

5. Later, we create another for loop, this time containing an if statement, for traversing through all the adjacent elements and to check whether the current element is greater than the next element. The condition of the if statement lst[j]>lst[j+1] always returns a boolean value (True or False) and the code inside the if statement only runs when this condition is True. We use the greater than operator > to check the values. When this is true, we swap the elements by setting the current element and assigning to it the value of the next element and vice-versa. Since lst is an alias for a list, to look inside lists we use square brackets []. Then we set the swap variable as True, implying that now a swap has occurred. In case no swap occurs, no change happens to the swap variable.

6. After we get out of the second for loop, we check for any swaps. For this, we check the swap variable. And again use an if statement and the equality operater == to check for any swaps. If the swap variable is False, it implies no swaps and therefore, we break out of the entire main for loop using the break statement. We use this statement whenever we want to get out of any loop in Python.

7. After getting out of the final for loop, we use the print() function and pass in the parameter lst to print the final sorted list. And again, since it's a function definition, we use the temporary variable, which is the parameter named lst.

8. In the example above, we use a list named y to test our bubblesort function. This list has 12 elements. To use the function (or in formal terms, to call the function), we type the name of the function, followed by parenthesis and inside it, we pass in the name of the list we want to sort.

Running the above program gives the following output.

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]

Complexity and Runtimes

• Big-O notation: In the worst case scenario, the bubble sort algorithm has a running time n square. This is because, at maximum, we go through the unsorted list 'n' number of times and traverse through all elements 'n-i-1' times. As 'n' gets larger and larger, we tend to ignore the constants. So in the end, the total number of steps the algorithm goes through is (n)x(n) i.e n squared.

• Big-Omega notation: In the best case scenario, the bubble sort algorithm has a running time of 'n'. This is because, at minimum, even when all elements of the list are sorted, we still have to go through the list once to check.

Applications of Bubble Sort

• Bubble sort is an algorithm that detects even marginally small errors in arrays/lists that are not completely sorted. This is used in computer graphics.

• On marginally small data sets, bubble sort algorithm fares better than selection sort in terms of time complexity.

References