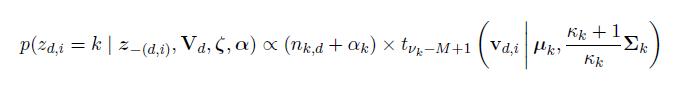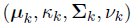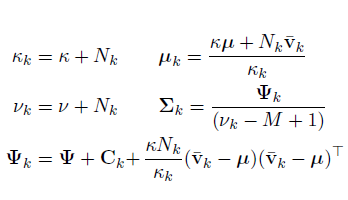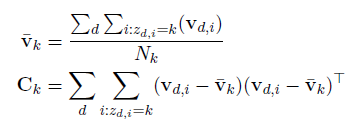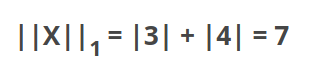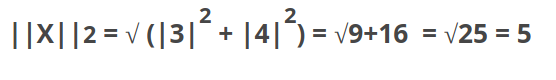Simplifying "Gaussian LDA for Topic Models with Word Embeddings"

Reading time: 40 minutes

The aim of the article is to explain the core concepts explained in the research paper "Gaussian LDA for Topic Models with Word Embeddings" by Rajarshi Das, Manzil Zaheer, Chris Dyer (associated with Carnegie Mellon University) in a easy fashion for beginners to get deep understanding of this paper.

Introduction

LDA is a statistical method where the corpora(collection of documents) is considered as the collection of small number of topics and the topics are considered as a sparse distribution of it on the words. Though this method produces remarkable results, it would be better if we can obtain semantic coherence between topics from this method. Semantic coherence is the relationships between various topics present in the documents. However this very useful semantic coherence is not a part of LDA and even if there are some observations found, they are not intentional by the algorithm. They are just accidental.

In this paper, we developed a variant of LDA which operates on continuous space word embeddings. This means that the discrete set of words present in the corpora are converted into continuous vector space where each word that is present in the corpus is embedded to a real number. This task is accomplished by using multivariate Gaussian distribution on the corpora which utilizes the mean and covariance matrices of the words. This enables them to obtain the semantic coherence between words.

The word embeddings thus produced were proved to be able to obtain the semantic coherence by Agirre et al., Mikolov et al. This happens because a Gaussian distribution by nature captures the centrality of the words present based on its usage and the related words are present close to each other in the text. Thus it extracts the existing preference of semantic coherence between words in the corpus.

A traditional LDA model carries a huge disadvantage that it assumes fixed number of vocabulary. It cannot consider the Out Of Vocabulary words obtained from documents that were not initially fed to the corpus. But the proposed method can handle unseen words with a small bias of using the topics already assigned in the other documents. Though topics only in prior documents are chosen, such topics are chosen with highest probability.

Gaussian LDA

Here, instead of working with a sequences of words, it would be better to work with a sequence of vectors. Thus the corpus is now converted into a vector space as follows. In Bayesian decision theory, if the posterior distributions p(θ | x) has similar pdf as the prior probability distribution p(θ), the prior and posterior are then called conjugate distributions and the prior is called a conjugate prior for the likelihood function. In the proposed model, we placed these conjugate priors on the following values: a Gaussian distribution with centre at zero for the mean and an inverse Wishart distribution for the covariance. In Bayesian statistics, an inverse Wischart distribution is used as conjugate prior for the covariance matrix of a multivariate normal distribution.

Since our words are in string format, we need to convert into a vector space. we need an analytical method to obtain it from the set of documents. We can obtain it using a method known as Gibbs Sampler method. Gibbs Sampler is a Markov Chain monte Carlo algorithm for obtaining a sequence of observations which are approximately from a specified multivariate probability distribution, when direct sampling from the documents are difficult [as already mentioned that they are available in text format]. The sampling equation is given below

More information about this equation can be found in the paper "Finding scientific
topics" by T. L. Griffiths and M. Steyvers.

The first portion of the above mentioned equation represents the probability of a given topic k in the document d and the second portion represents the probability of assigning the word k to a word vector v(d,i) with the given current topic assignments. They are expressed by a multivariate t distribution with parameters as

The first portion is basically an expression of LDA model. Thus the model is an alternation of LDA model with an additional term to convert the words into word vectors based on multivariate t distribution with the above mentioned parameters. The parameters can be expressed as below.

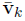
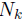
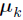
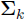
In the above equations, is the sample mean and is the scaled form of covariance of the vectors with assigned topics k. represents the total number of words assigned to a particular topic k in a given set of documents. Then the parameters and represents the posterior mean and covariance of the topic distribution.

Experimentation

The model is then experimented to determine if the topics generated are really coherent and meaningful. It is also performed to make sure that the model is able to identify topics for words in new unseen documents. The experimentation is done on preprocessed data. In other words, the text dataset is cleaned, tokenized and converted to lowercase. Here the datasets used are 20 Newsgroup and Neural Information Processing System (NIPS). Let us now see the performance of the model in determining coherence between different topics in the existing documents.

Topic Coherence

Quantitative analysis

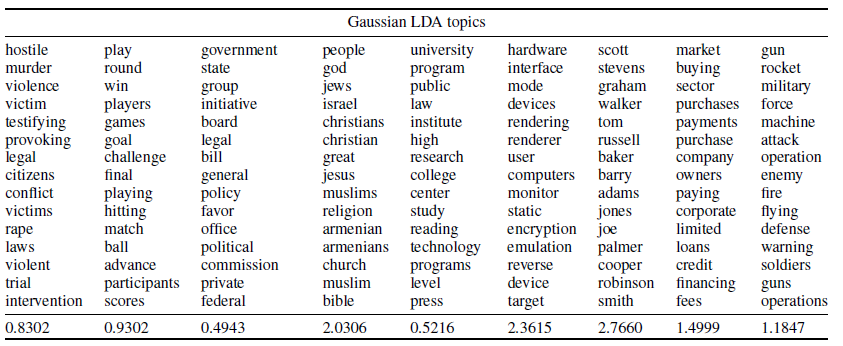
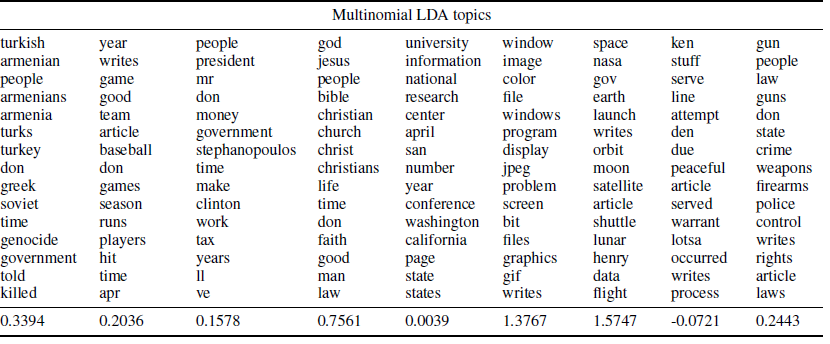
In traditional LDA, the topics are represented as discrete elements. Thus their probability distribution exists in the form of probability mass function. Whereas in the proposed model, we represent the words as a continuous distribution. Thus its probability distribution exists in the form of probability density function. In order to measure the topic coherence, we use Pointwise Mutual Information (PMI) of topic words with respect to wikipedia articles as explained by Newman et al in 2009. They extracted the co-occurrance statistics of the topic words from wikipedia and computed the score of a particular topic by averaging the individual score (continuous variable as mentioned earlier) of the top 15 words classified under that topic.The higher the value of PMI, higher is the coherence of topics as it implies that topics occur more closely to each other. The below tables show the PMI scores for topics generated by both traditional LDA and our proposed model (Gaussian LDA).

It is evident from the tables that Gaussian LDA performs better with a PMI score 275% than that of traditional LDA.

Qualitative Analysis

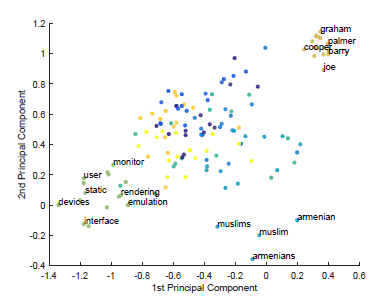
We can also judge from the above tables that the Gaussian LDA was able to identify certain topics such as 'sports', 'government', 'religion', 'finance' etc which are similar to human perception. The words in each columns are arranged based on the density assigned to them by posterior predictive distribution. It is also wonderful to note that Gaussian LDA was able to identify human names in a separate column and it has the highest PMI value. But the traditional LDA bags behind all these and its performance is very low. We also performed Principal Component Analysis over all the word vectors and first two components are shown below. This shows that density alloted to them are significantly separated on its own.

Performance on unseen documents

While working on traditional topic modeling algorithms, whenever we feed a new unseen document, it omits the unseen words which might hold some important information for our purpose. But our model is capable of assigning them values as we use continuous distribution for our word vectors. In order to perform this, we split a part of the document and replace some of its words with its synonyms (made sure that the synonyms are not present in the corpus). Also these transformation from given words to its synonyms does not occur through human intervention. It is done through two techniques and made into two test datasets for evaluation purpose.

In the first method, we use Paraphrase Database to obtain the equivalent lexical paraphrase of the words. The database consists of 169 million paraphrase pairs of which 7.6 million are lexical (one gram) paraphrases. The dataset is available in varying sizes from S to XXXL with increasing order of size and decreasing order of paraphrase confidence. For our purpose, we will be using L size.

In the second method, we use WordNet a large human annotated lexicon for english which groups all the synonyms under synsets. In this process, we first use Stanford POS tagger to tag each of the words according to their parts of speech. Then we replace it with first occurring word in the synset that has not been a part of the corpus.

On using the 20 News dataset which contains test corpus of 188694 words, a total of 21919 words (2741 distinct words) are replaced by Paraphrase Database (First method) and a total of 38687 (2037 distinct words) are replaced by Wordnet (Second method).

Evaluation

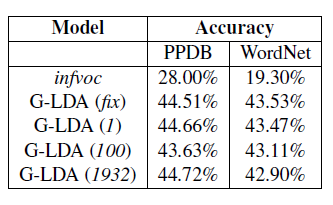
Traditional topic modeling algorithms including LDA cannot handle OOV words and so we cannot compare our model with them. So, we will be comparing our performance with an extension of LDA (infvoc) proposed by Zhai and Boyd-Graber in 2013. In this model (infvoc), the value of probabilty assigned is directly proportional to the number of occurances of the word. therefore, it assigns comparatively lower probability to newer occurring words. Whereas our model assigns a higher probability if the new words corresponds with such word embeddings.

In order to evaluate our mode, we try to classify the data into 20 groups based on the distribution we have modeled. THis can be used to determine the performance of our model. An online algorithm is a one which takes input in serial fashion instead of taking it as a whole ( works like an interpreter). Our comparison model (infoc) is an online algorithm which witnesses every test word freshly everytime. So we convert our model into online version. We input the test documents in varying batch sizes and use multi class logistic regression classifier. We perform the experiments in batch sizes of 1, 100 and 1932 and the results are tabulated below.

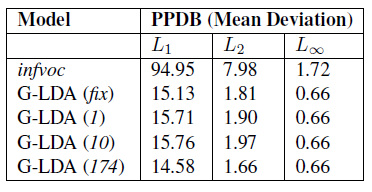
As our model works better in all the experiments, we can understand that our model is able to find new words also in the documents. We also need to evaluate the quantitative difference between the original documents and the alters documents (synonyms). We can calculate the norm and compare them for this purpose. A norm is the total length of vectors present (i.e. the magnitude of vector). We perform L2, L3 and L-infinity norms on the difference between the word vectors of original document and the altered document. The lower the norm, higher is the similarity between the documents. By observation, we can understand that Gaussian LDA performs better than infvoc. The results are tabulated below.

Conclusion

Thus, we can conclude that our proposed Gaussian LDA is able to develop coherent relationships between the generated topics. It also works on unseen words in a better fashion. This model can be applied in many other fields also.

Annexure

L1 norm

L1 norm is the sum of magnitude of vectors in space.

L2 norm

Also known as Euclidien norm, it is the shortest distance from one point to another.

L-infinity norm

L-infinity norm represents the largest magnitude among each element of a vector.

If a vector is represented as [10, -22, 16], the L-infinity norm of the vector is 22.

Read more

• Gaussian LDA for Topic Models with Word Embeddings by Rajarshi Das, Manzil Zaheer and Chris Dyer from Carnegie Mellon University
• Topic Modelling Techniques in NLP by Murugesh Manthiramoorthi
• Topic Modeling using Non Negative Matrix Factorization (NMF) by Murugesh Manthiramoorthi
• Topic Modeling using Latent Semantic Analysis by Murugesh Manthiramoorthi
• Topics Modeling using Latent Dirichlet Allocation (LDA) by Harsh Bansal

With this article at OpenGenus, you must have got a strong understanding of this research paper at hand. Enjoy.