
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes | Coding time: 12 minutes
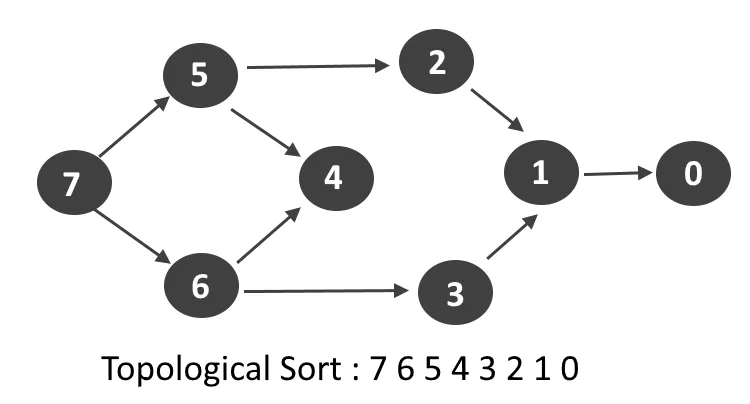
Another sorting technique?!
No, topological sort is not any ordinary sort. It is a linear ordering of vertices in a Directed Acyclic Graph (DAG) such that for every directed edge u->v, vertex u comes before v in the ordering.
A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering.
In this article, we will explore how we can implement Topological sorting using Kahn’s algorithm.
 Read about DFS solution for Topological Sorting
Read about DFS solution for Topological Sorting
Idea behind Kahn’s algorithm
A DAG G has at least one vertex with in-degree 0 and one vertex with out-degree 0.
Proof:
Consider a directed acyclic graph G.
- G does not contain a cycle -> all paths in G are of finite length
- Let S be the longest path from u (source) to v (destination).
- Since S is the longest path there can be no incoming edge to u and no outgoing edge from v
- If the above situation had occurred then S would not have been the longest path (contradiction)
->in-degree(u) = 0 and out-degree(v) = 0
Algorithm Overview
- Output the nodes with indegree 0 in any order.
- Remove them and their outgoing edges. We now have a new set of nodes with indegree 0 which are the children of the earlier nodes.
- Output them in any order and remove them.
- This goes on.
Stepwise Explanation
-
Step 1: Make an AdjList with the current indegree of each node and initialize the count of visited nodes as 0.
-
Step 2: Make a queue of the set of nodes with indegree 0 (Enqueue operation)
-
Step 3: Remove a vertex from the queue (Dequeue operation) and then:
- Increment count of visited nodes by 1.
- Reduce in-degree by 1 for all nodes adjacent to it.
- If in-degree of an adjacent node is reduced to zero, then add it to the queue.
-
Step 4: Repeat Step 3 until the queue is empty.
-
Step 5: If count of visited nodes is not equal to the number of nodes in the graph then the topological sort is not possible for the given graph.
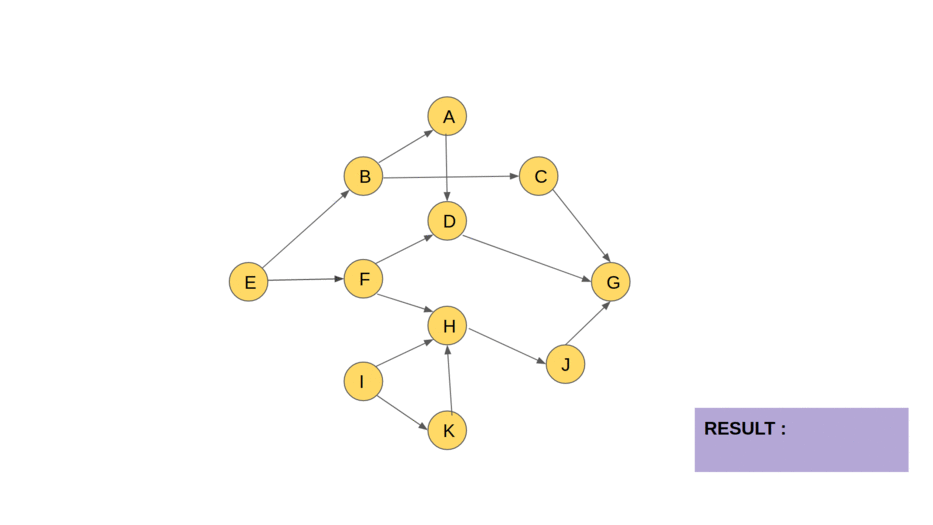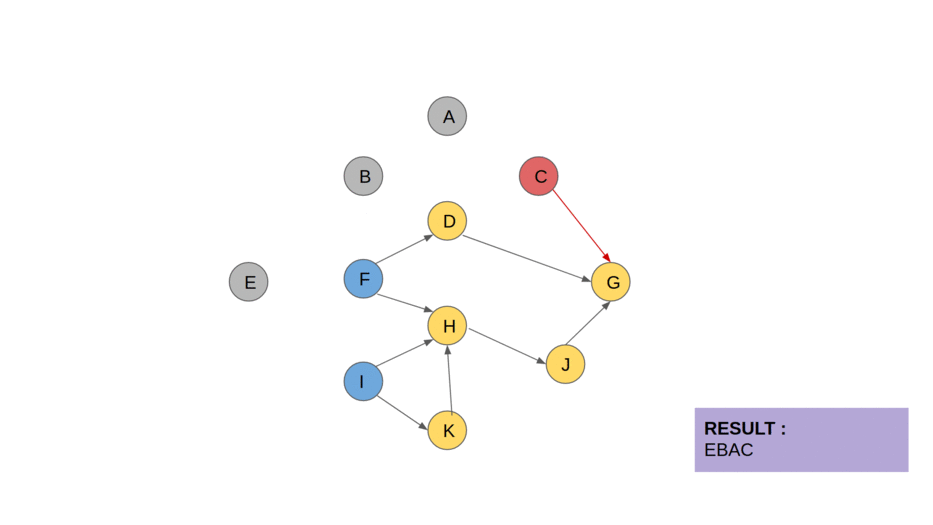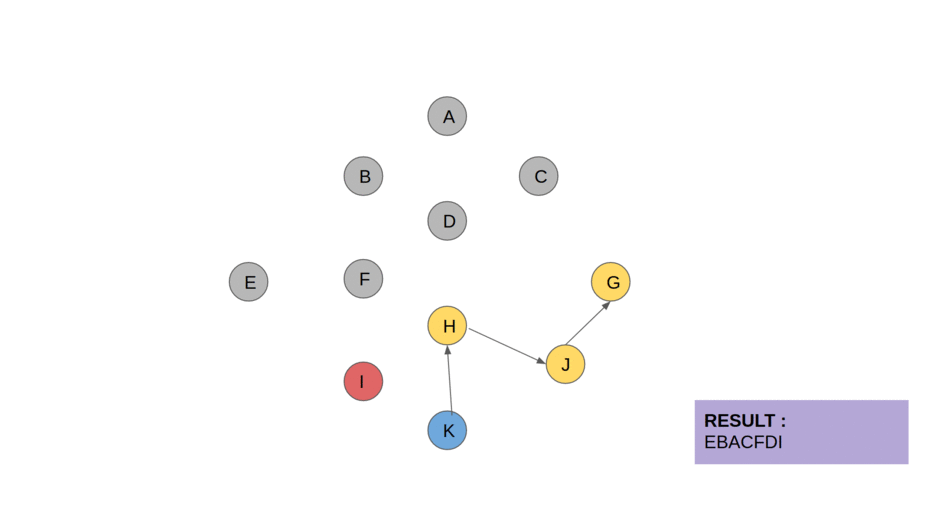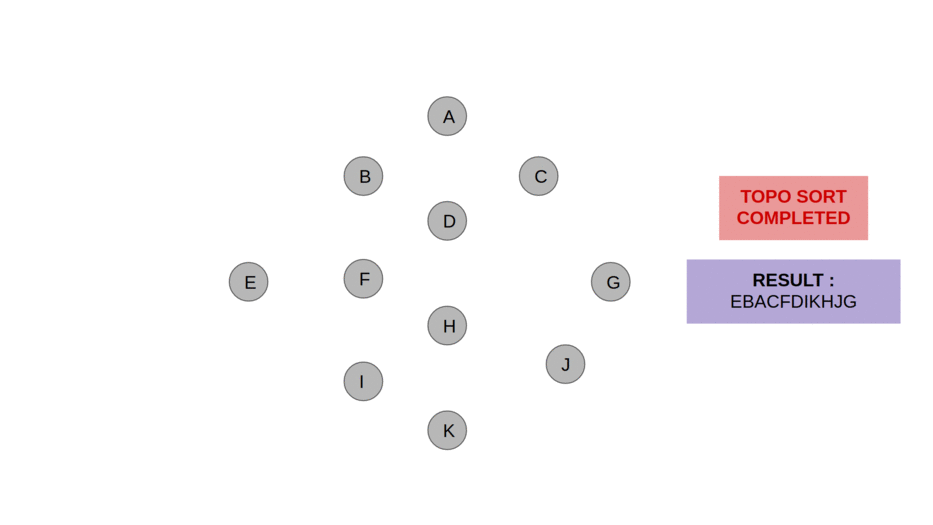
Let's simulate it!
The colouring of the vertices and edges in the animation is as follows :
-
YELLOW: Regular DAG.
-
BLUE: vertices with in-degree=0, during any iteration. These are the vertices pushed into the queue.
-
RED: vertex chosen to be explored (One among the blue vertices)
-
GREY: vertices that have been explored and included into the topologically sorted order
Calculation of Indegree
Traverse the array of edges and simply increase the counter of the destination node by 1.
Pseudo Code
for each node in Nodes
indegree[node] = 0;
for each edge(src,dest) in Edges
indegree[dest]++
Time Complexity
There are parts that are to be considered while calculating the time complexity of the above algorithm.
-
Indegree Calculation:
The initialization of indegrees to 0 will be executed V number of times. The inner for loop will be executed for each edge ie E number of times.
-
Algorithm:
Each node is put in the queue exactly once (V number of times totally). As it is dequeued, the degree is reduced for all its edges (E times cumulatively).
Thus overall time complexity is O(V+E).
- Worst case time complexity:
Θ(V+E) - Average case time complexity:
Θ(V+E) - Best case time complexity:
Θ(V+E) - Space complexity:
Θ(V)
Implementation
Following is the C++ implementation:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int x, y, e,v;
cin >> v >> e; // Number of vertices and edges
vector <int> AdjList[v]; // Step 1: Initializing AdjList
vector<int> indegree(v, 0); // Step 1: Initializing indegrees to 0
queue <int> q;
int visited_nodes = 0; // Step 1: Visited nodes initialized to 0
for(int i=0; i < e; i++)
{
cin >> x >> y;
indegree[y]++; // Incrementing indegree
AdjList[x].push_back(y); // Add the edge x -> y to adjacency list
}
for(int i = 0; i < v; i++)
if(indegree[i]==0) q.push(i); // Step 2: Add all indegree 0 nodes to queue
while(!q.empty()) // Step 3: Remove vertex from queue
{
visited_nodes++; // Step 3.1 Incrementing count of visited nodes
for(auto x: AdjList[q.front()])
{
indegree[x]--; // Step 3.2 Reduce indegree of adjacent node
if(indegree[x]==0) q.push(x); // Step 3.3 Push adjacent node with indegree 0
}
cout << q.front()<<" ";
q.pop();
} // Step 4: Repeat until queue is empty
if(visited_nodes != v) // Step 5: if visited nodes are not equal to number of vertices, cycle exists
cout<<"\nCycle exists, cannot do further topological sort";
}
Applications
Sooo.. does it tell us which came first, the chicken or the egg? xD
Topological Sorting is mainly used for
- Finding deadlocks in OS
- Scheduling jobs from the given dependencies among jobs.
- Instruction scheduling
- Ordering of formula cell evaluation when recomputing formula values in spreadsheets
- Logic synthesis
- Determining the order of compilation tasks to perform in makefiles
- Data serialization
- Resolving symbol dependencies in linkers
- Finding cycles in a graph
10.Finding prerequisites of a task
Kahn you solve our little quiz?
Question 1
Topological sort of a Directed Acyclic graph is?
The topological sort of a graph can be unique if we assume the graph as a single linked list and we can have multiple topological sort order if we consider a graph as a complete binary tree.
Question 2
Topological sort is equivalent to which of the traversals in trees?
In pre-order traversal of trees, we process the root first and then child from left to right.
With this article at OpenGenus, you will have a complete idea of Topological Sorting using Kahn's Algorithm.
