
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will be designing a LFU (Least Frequently Used) Cache using different Data Structures such as Singly Linked List, Doubly Linked List, Min Heap and much more.
Contents
- Introduction to LFU (Least Frequently Used) Cache
- Properties
- Solving the Problem
- Implementation of the functions get(keyelement) and set(keyelement,value).
- Using Map
- Using Singly Linked List
- Using Doubly Linked List to Make the Access time O(1).
- Using Min Heap
- Practical Example of LFU Cache
Pre-requisites:
Introduction to LFU (Least Frequently Used) Cache
Least frequently used algorithm is used for managing memory in computers.
In this method, we will keep a count (frequency) of number of times a block of memory has been accessed. When the capacity is reached (i.e, when the cache is full) it will replace the least frequently used block with new one.
The core idea of LFU (Least Frequently Used) Cache is the elements that are more frequently accessed should be in the cache to reduce access time. Elements that are relatively less frequently used are removed for the cache if another element needs to be inserted.
There are some downsides to this cache like if a new element is accessed, it will require significant number of repeated access to make it enter the cache as the frequency should be higher than already existing elements.
In some cases, LFU (Least Frequently Used) Cache can be the best performing cache as well.
Properties
In LFU (Least Frequently Used) Cache, we need two functions which does the following operations:
get(keyelement) -- fetches the value corresponding to the key if it exists.If it donot exist inthe cache then it returns -1.
set(keyelement,value) --- If the key is not present in the cache,it will insert it into the cache.If the capacity is full the the least frequently used one is replaced.If two or more keys in the cache has same frequency then the which has come first will be replaced.
Solving The Problem
We have used different data structures to solve this problem. Let us see the different approaches:
Let us first take one of the data structure that we all have learned first in our DS journey: Array
So what all we need?
- The key
- it's corresponding value
- frequency of key
- timestamp at which key is accessed or updated.
This time stamp is essential when we need to replace a key but two or more keys have same frequency, then we have to remove the key with least timestamp, that is the one which came first
So, firstly let us declare an array of size equal to the capacity of the cache.
The array will have the above defined elements.
struct arr{
int key;
int value;
int freq;
int timestamp;
}arr[100];
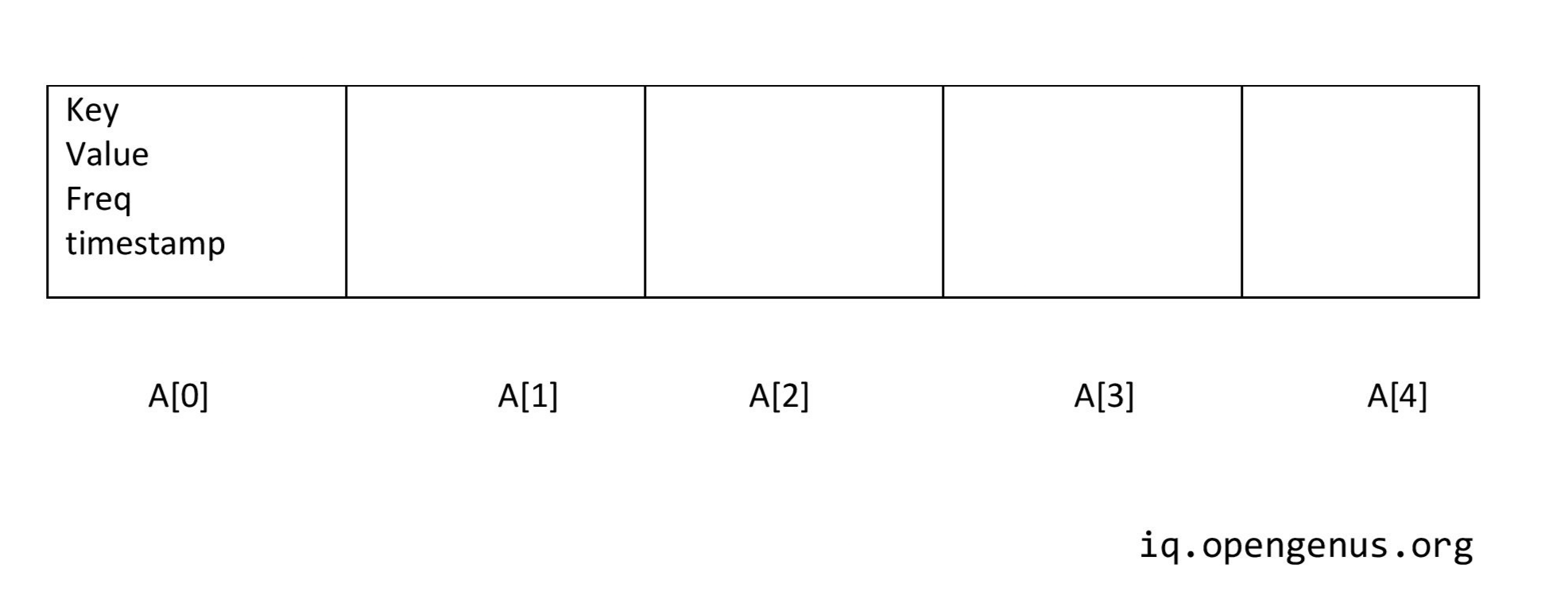
The use of freq and timestamp is to find out the least frequently used element.
Implementation of the functions get(keyelement) and set(keyelement,value)
get(keyelement)---When we are given the key,we will traverse the array and compare each key element of the array with the given key.If found we will increase the frequency of that element by 1 and also the timestamp is updated.If not found we will return -1.
set(keyelement,value)---If the array is full then we will remove the least frequently used one with the help of freq by traversing the array and finding the key with least value of freq and deleting it.If two or more elements have same frequency the the one which came first will be replaced(that is the one with oldest timestamp).
If the array is not full then we will insert the new element with frequency 1 and timestamp as 0.For the element in the array,we will increase the timestamp by 1.
Here the time complexity for getting key element is O(n) in worst case as we have to traverse the array.
Time complexity of set key element is also O(n).
Space complexity is O(1) as no auxillary space is used.
But this is not an efficient way.So we will move on.
Throughout the journey we will see ways to optimise our approach that is to find the most efficient one.
Using Hash Map
Let us consider 2 Hash maps.
The first one stores key value pairs and 2nd stores the frequency or counts of access.
Now here, when the capacity of the cache is full,we need to delete one element.For that we need to find the least frequently used one.For that we have to iterate through the frequncy map to find the lowest frequency.This will result in a time complexity of O(n).
Space complexity is O(1) for the operations. The cache needs constant space as well.
If more than one key with same frequency exists then we cannot find the least recently used one as we donot store the elements based on the order in which they come.
As a solution to this problem,we will make the frequency map as a sorted one with frequency as the key and the value as a list of elements with the same frequency.
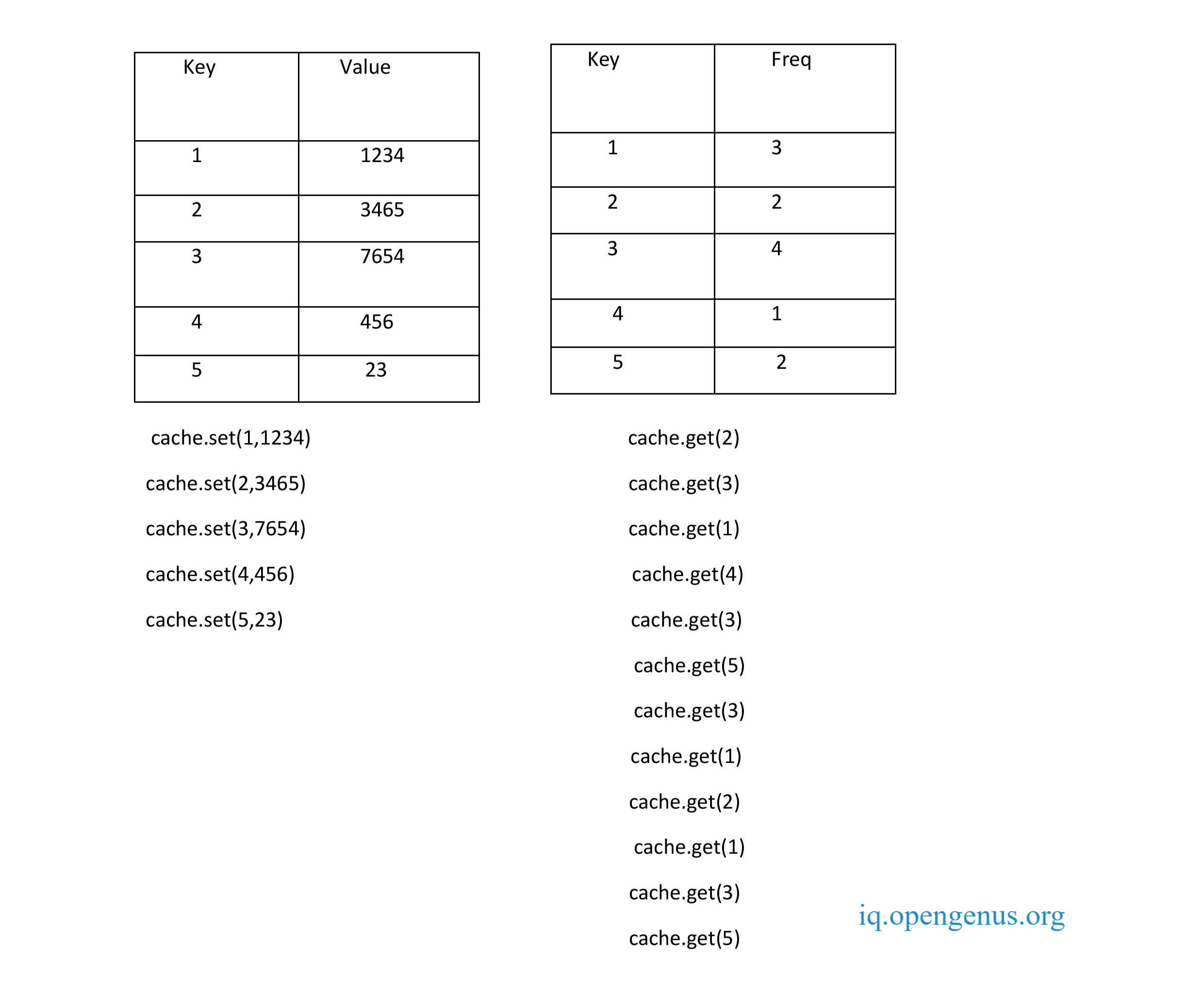
Now, how to store the values of the frequency?For that we will use linked list:
Using Singly Linked List
Here we can find the least frequency in O(1) time as we have sorted the frequencies.If multiple keys have same frequency we can find the least recently used one as it will be the first element in the singly linked list corresponding to that frequency.We can delete it in O(1) time.We can also insert with O(1) time complexity.
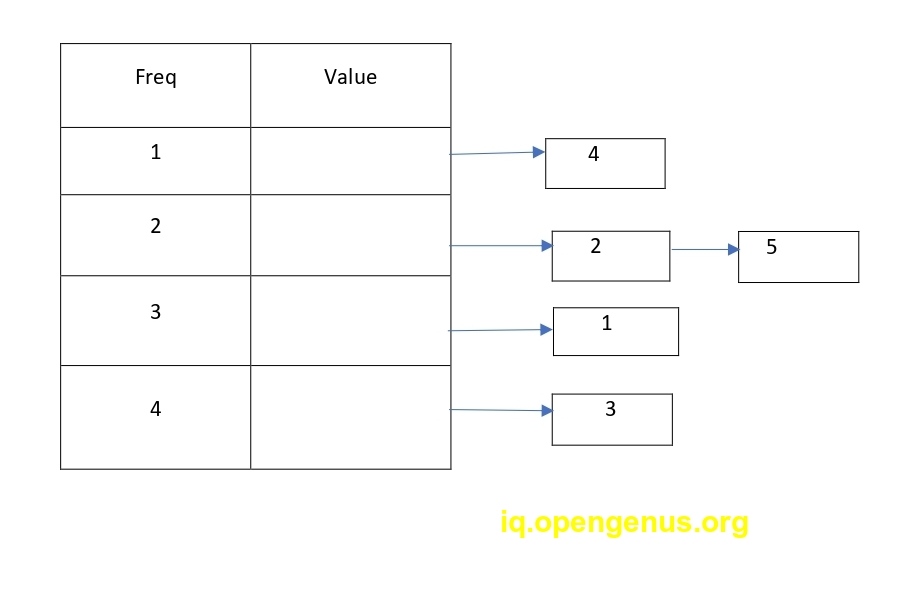
But when need to access an element,we need to travese the singly linked list find the element and move it to the next frequency.This will take O(n) time in the worst case.
We have to deduce a method to access the element without traversing the array,so that we can delete the element in O(1) time and move it to the end of singly linked list of next frequency.
How will we solve this problem? For that let us make use of Doubly Linked Lists.
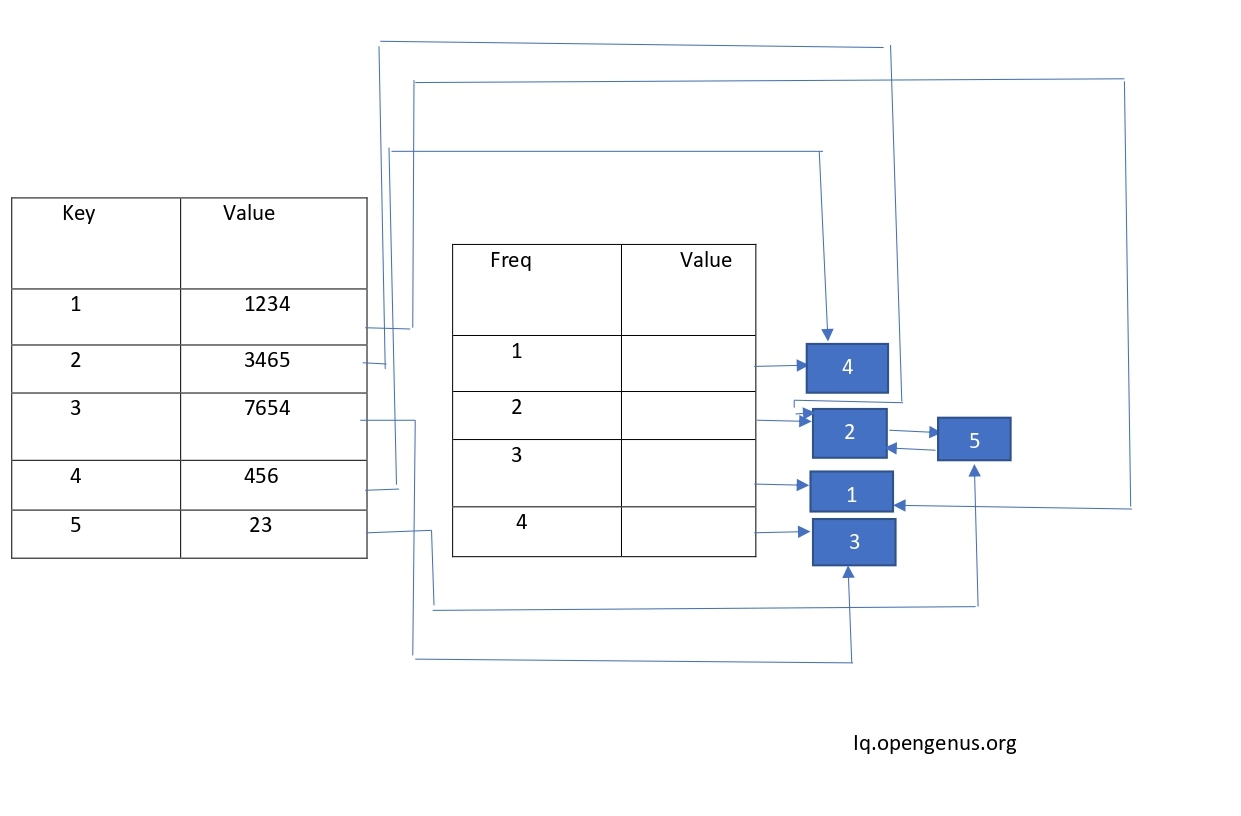
Using Doubly Linked List to Make the Access time O(1).
We will make a node with the value of key and the key.The key in the value map points to the key node in the frequency map.Thus the singly linked list is converted to Doubly linked list.
This one is better than the previous one in terms of access time.
Using Min Heap
Heap is a data structure which is a complete binary tree and is either min heap or max heap.
Min heap has the parent less than the children.
The benefit of minheap is that the insertion, deletion and updation takes place in O(log(n)) time complexity.
Space complexity is O(1).
Therefore,this is the best method.
Let us use C++ to find the solution.
We need:
-
To store the indices of the cache block we use a hashmap. This help us to search in O(1) time complexity.
-
To represent the cache we use a vector of integer pairs.Each pair has the block number and frequency(no of time it is accessed).To access the least frequently used block with O(1) time complexity we order the vector in the form of min heap.
Let us see the code:
// Part of iq.opengenus.org
#include <bits/stdc++.h>
using namespace std;
// function for swapping two pairs
void swap(pair<int, int>& a, pair<int, int>& b)
{
pair<int, int> temp = a;
a = b;
b = temp;
}
// Used to return the index of the parent node
inline int parent(int i)
{
return (i - 1) / 2;
}
// used to return the index of the left child node
inline int left(int i)
{
return 2 * i + 1;
}
// used to return the index of the right child node
inline int right(int i)
{
return 2 * i + 2;
}
void heapify(vector<pair<int, int> >& v,
unordered_map<int, int>& m, int i, int n)
{
int l = left(i), r = right(i), minim;
if (l < n)
minim = ((v[i].second < v[l].second) ? i : l);
else
minim = i;
if (r < n)
minim = ((v[minim].second < v[r].second) ? minim : r);
if (minim != i) {
m[v[minim].first] = i;
m[v[i].first] = minim;
swap(v[minim], v[i]);
heapify(v, m, minim, n);
}
}
// To Increment the frequency
// of a node and rearranges the heap
void increment(vector<pair<int, int> >& v,
unordered_map<int, int>& m, int i, int n)
{
++v[i].second;
heapify(v, m, i, n);
}
// To Insert a new node in the heap
void insert(vector<pair<int, int> >& v,
unordered_map<int, int>& m, int value, int& n)
{
if (n == v.size()) {
m.erase(v[0].first);
cout << "Cache block " << v[0].first
<< " removed.\n";
v[0] = v[--n];
heapify(v, m, 0, n);
}
v[n++] = make_pair(value, 1);
m.insert(make_pair(value, n - 1));
int i = n - 1;
// For inserting a node in the heap by swapping elements
while (i && v[parent(i)].second > v[i].second) {
m[v[i].first] = parent(i);
m[v[parent(i)].first] = i;
swap(v[i], v[parent(i)]);
i = parent(i);
}
cout << "Inserting " << "Cache block"<<value \n;
}
// used to refer to the block value in the cache
void refer(vector<pair<int, int> >& cache, unordered_map<int,
int>& indices, int value, int& cache_size)
{
if (indices.find(value) == indices.end())
insert(cache, indices, value, cache_size);
else
increment(cache, indices, indices[value], cache_size);
}
int main()
{
int cache_max_size = 4, cache_size = 0;
vector<pair<int, int> > cache(cache_max_size);
unordered_map<int, int> indices;
refer(cache, indices, 1, cache_size);
refer(cache, indices, 2, cache_size);
refer(cache, indices, 1, cache_size);
refer(cache, indices, 3, cache_size);
refer(cache, indices, 2, cache_size);
refer(cache, indices, 4, cache_size);
refer(cache, indices, 5, cache_size);
return 0;
}
The output of the above code will be:
Inserting cache block 1.
Inserting cache block 2.
Inserting cache block 3.
Inserting cache block 4.
Inserting cache block 5.
Practical Example of LFU Cache
Let us consider the example of accessing the internet.
We need to store the static resources such as images,CSS Stylesheets and javascript code as almost every request require them. In this case, LFU (Least Frequently Used) Cache is the preferred cache.
And that's it. Yay we have reached the end of this article at openGenus. Good work Guys.
