Linear Activation Function

In this article, we have explored Linear Activation Function which is one of the simplest Activation function that can be used Neural Networks.

Table of contents:

1. What are Activation Functions?
2. Why are Activation Functions required?
3. Linear Activation Functions
4. Comparison Between Linear Activation Function and Other Activation Functions

Prerequisite:

• Basics of Activation Function
• Types of Activation Function

What are Activation Functions?

Activation functions are mathematical equations that determine the output of a neural network. They basically decide to deactivate neurons or activate them to get the desired output, thus the name, activation functions.

In a neural network, the weighted sum of inputs is passed through the activation function.

Y = Activation function(∑ (weights*input + bias))

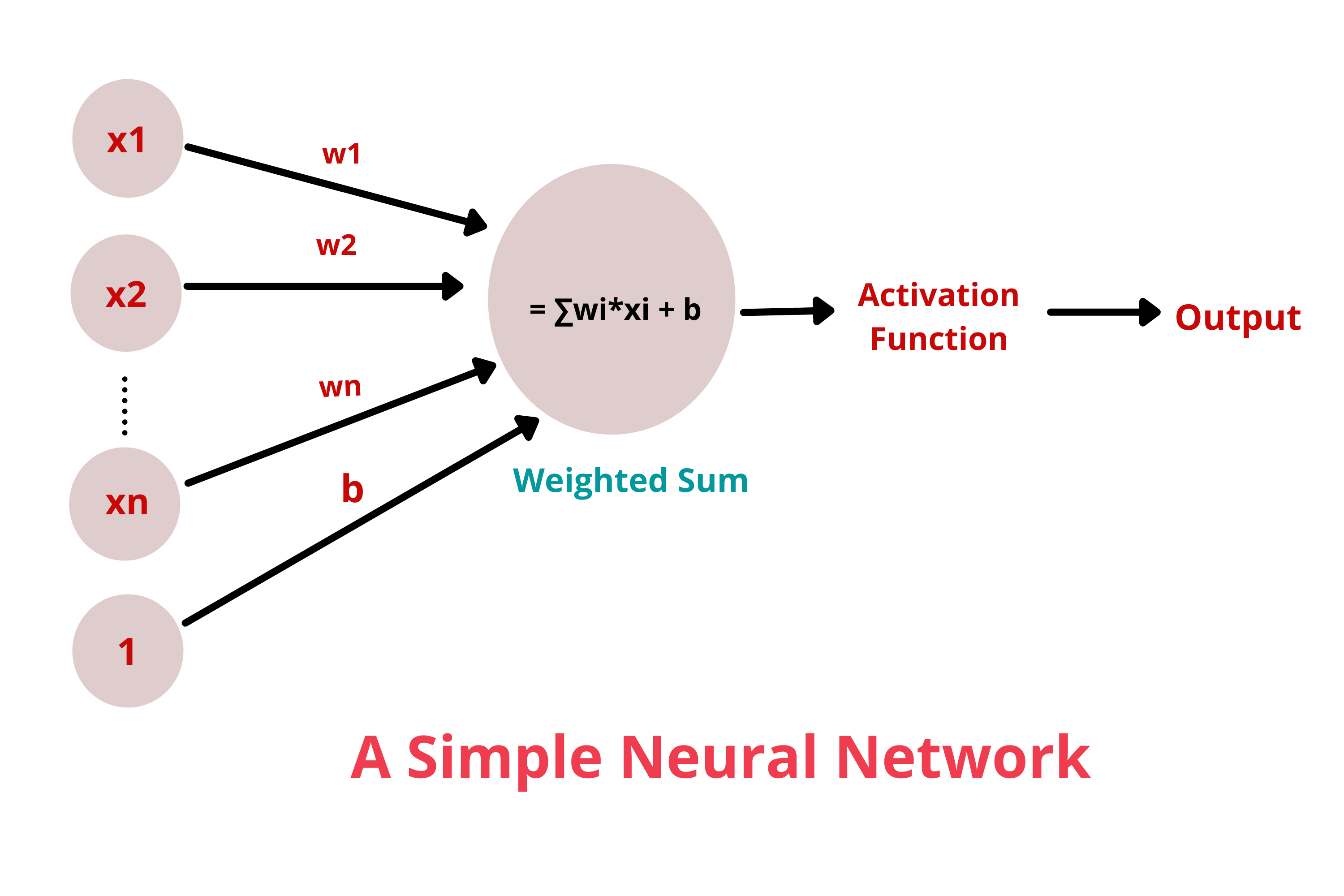
Why are Activation Functions required?

Activation Functions convert linear input signals to non-linear output signals. In addition, Activation Functions can be differentiated and because of that back propagation can be easily implemented.

Linear Activation Functions

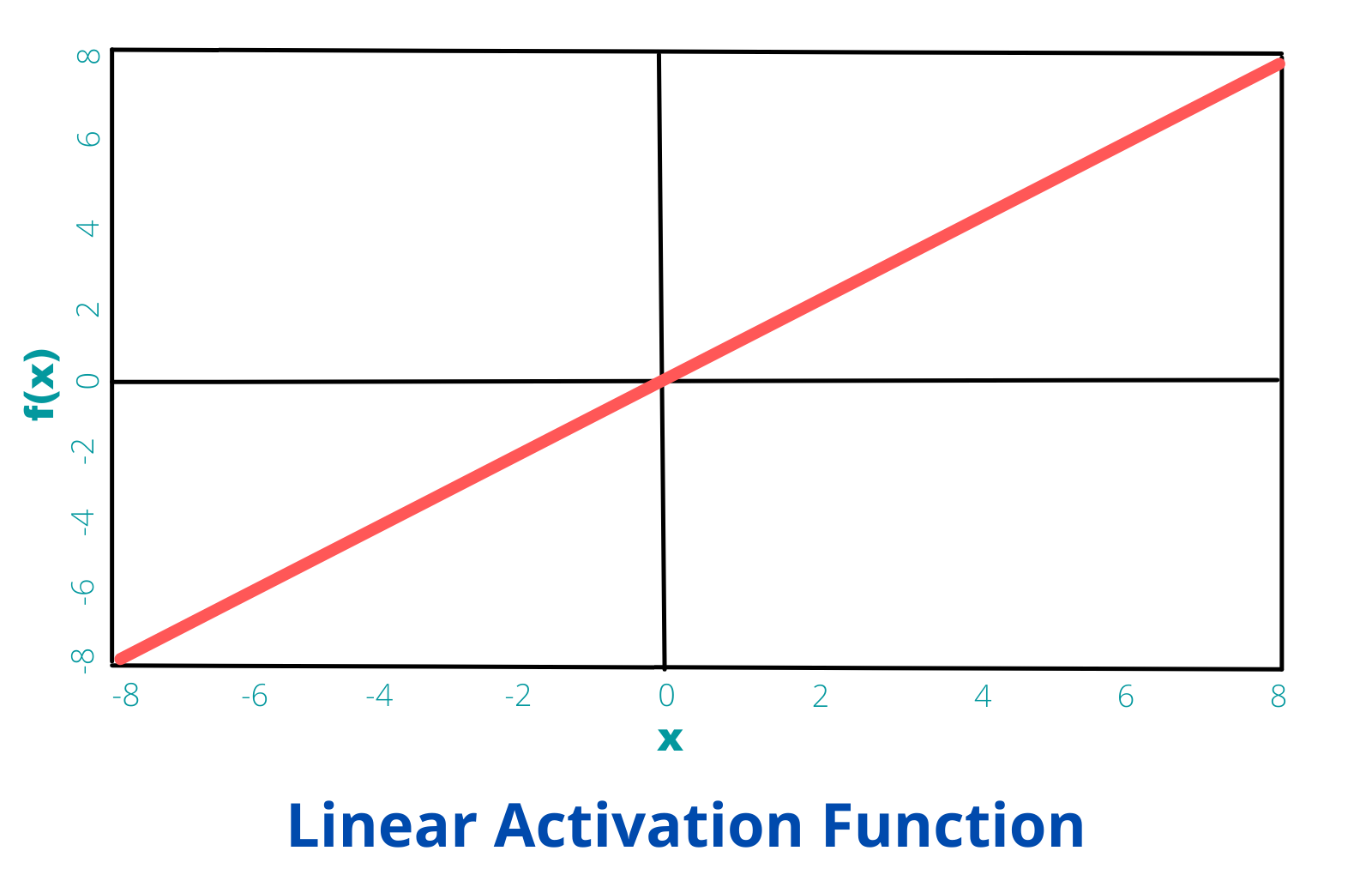
It is a simple straight-line function which is directly proportional to the input i.e. the weighted sum of neurons. It has the equation:

f(x) = kx

where k is a constant.

The function can be defined in python in the following way:

def linear_function(x):
    return 2*x
linear_function(3), linear_function(-4)

Output:

(6,-8)

The derivative of Linear Activation Function is:

f'(x) = k

which is a constant.

Unlike Binary Step Function, Linear Activation Function can handle more than one class but it has its own drawbacks.

The problem with Linear Activation Function is that it cannot be defined in a particular range. It has a range of (-∞, ∞). No matter how many layers the neural network has, the final layer always works as a linear function of the first layer. This makes the neural network unable to deal with complex problems.
Another problem is that the gradient is a constant and does not depend on the input at all. As a result during backpropagation the rate of change of error is constant. Thus the neural network will not really improve with constant gradient.

Comparison Between Linear Activation Function and Other Activation Functions

Conclusion

In this article at OpenGenus, we learnt about Linear Activation Function, its uses and disadvantages and also saw a comparison between different activation functions.