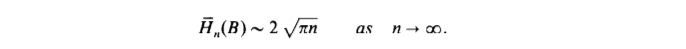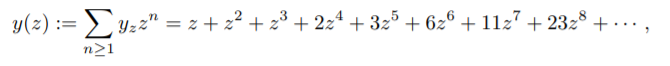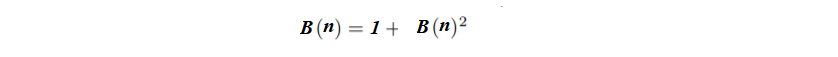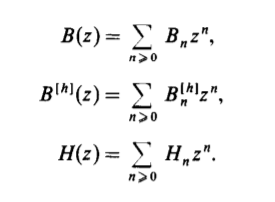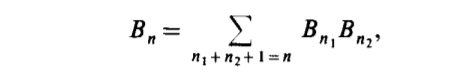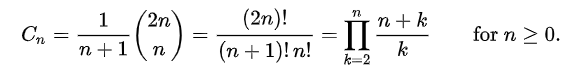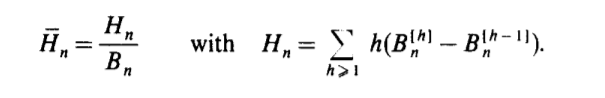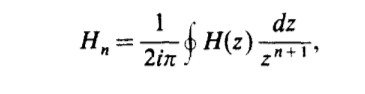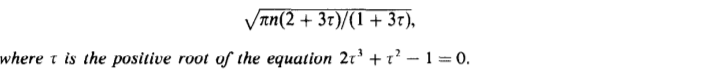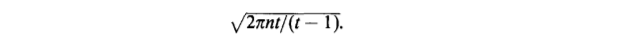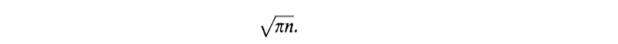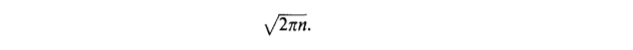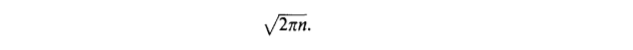In this article, we have explored an insightful approach/ algorithm to find the average height of Random Binary Tree which is of the order O(N^0.5). This will strengthen our understanding of binary trees and their applications.

Before we move further into the topic of discussion, let us revise the basics of a binary tree!

TABLE OF CONTENTS

• Points to recall
  • Size of a binary tree
  • Height in a binary tree
• Understanding the problem
• Average height of a random tree with 'n' nodes
  • Disposition
  • Tree traversal analysis
  • Generating function
  • General formula for all trees
  • Estimation towards constraining the general formula to Binary-trees
  • Algorithm
  • Implementation
  • Time-Complexity analysis
  • Space-Complexity analysis
• Summary
• Test your understanding

Reading time: 45 minutes | Coding time: 15 minutes

1) POINTS TO RECALL

This article only brushes over concepts of a binary tree that are required in the solution of the problem statement. Learn more from the Binary Tree article from OpenGenus.

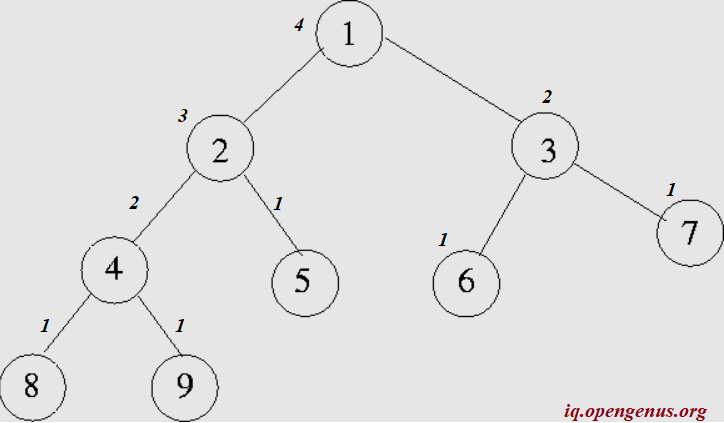
A binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.

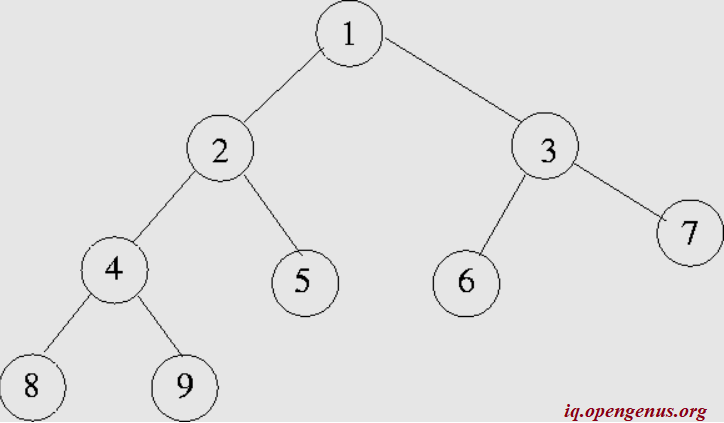
In the above example, node 1 is the root. There are 9 nodes in all and each node has either 0 or 2 child nodes.

1.1) Size of a binary tree:

The size of a binary tree is simply the number of nodes present. In the above example, the number of nodes are 9 and it is the size of the binary tree.

1.2) Height in a binary tree:

With respect to a binary tree, height can be defined at two level - node and the entire tree.

1. Height of a node: The height of a node is defined by the following relation:
   height(leaf_nodes) = 1
   height(internal_nodes) = 1 + max{(height(t1), height(t2)},
   where t1 = left_subtree and t2 = right_subtree.

Let us consider an example. In the above figure, let us find the height of node 2.
Node 2 is not a leaf node, so condition 2 is applied. THe left and right sub_tree are defined:

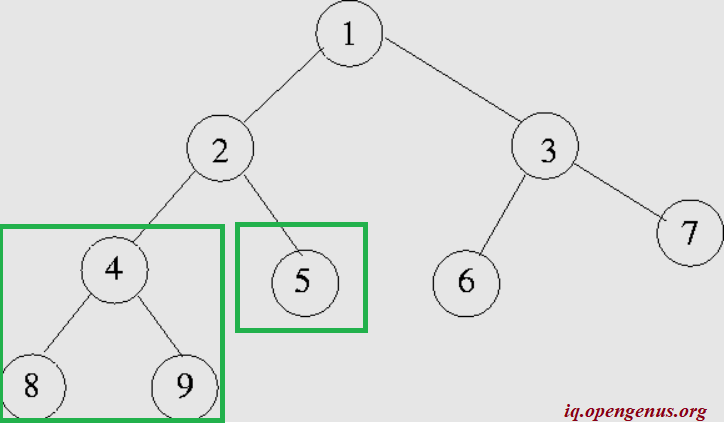
The root of the left-subtree(node 4) is not a leaf-node, so it is further split:

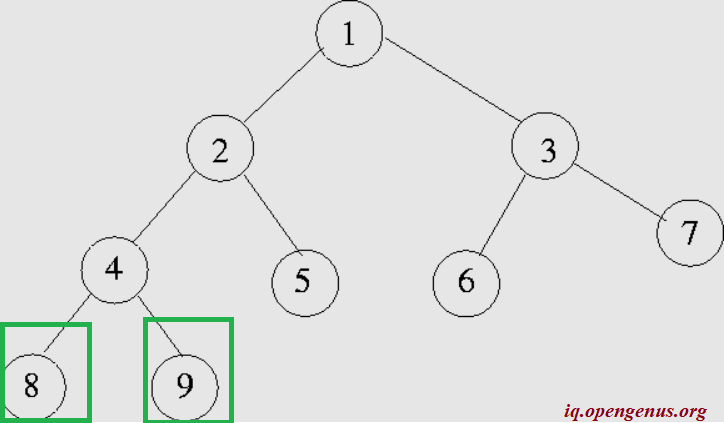
Now, we have the leaf_node, let us mark their height.

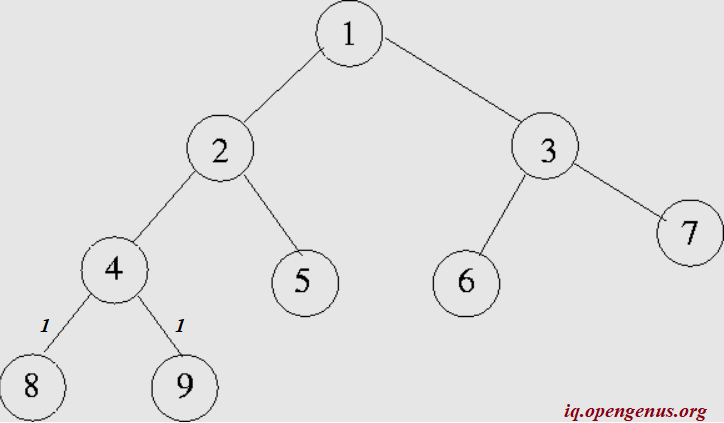
From this the height of the node 4 is 1+max(1,1) = 2.Similarly the height of node 5 is 1. Since we have the height of pre-requisite nodes, the height of node 2 can be calculated as
1+ max(height(left_subtree), height(right_subtree)
1+ max ( 2,1)
1+ 2 = 3

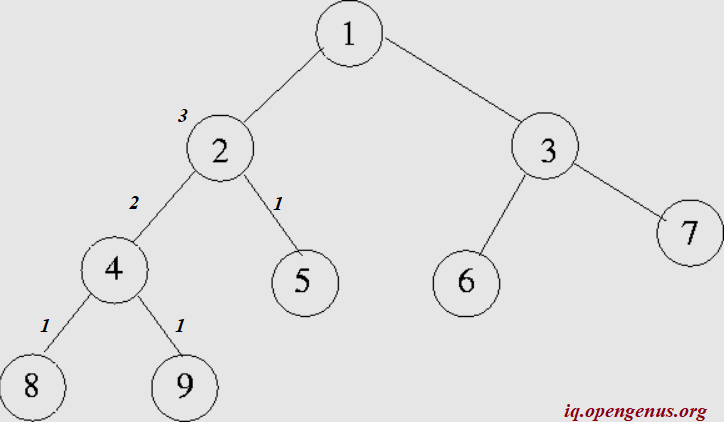
2. Height of the binary tree: The height of a binary tree is the height of the root node in the whole binary tree. In other words, the height of a binary tree is equal to the largest number of edges from the root to the most distant leaf node.

Let us find the height of the example binary tree by first applying condition 2.

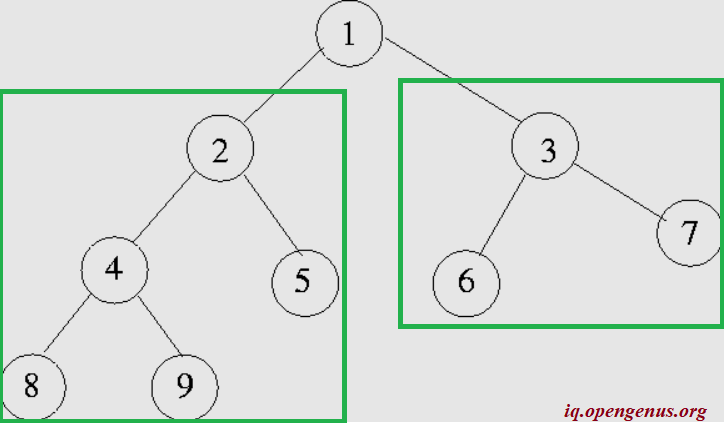
We are aware from our previous section that the height of the left_subtree is 3. Let us calculate the height of the right sub_tree (node 3). It is = 1+ max (1,1) =2
Hence, the height of the binary tree is
1 + max (3,2) =
1 + 3 = 4

Note: If all that we know about a binary tree is that there are n nodes in it, the tree can be constructed in many ways such that the height of the tree ranges from n-1 to floor(log n).
i.e maximum height of the binary tree of n nodes is n-1 and minimum height is floor(log2n)

Now that we understand how to calculate the height, let us move on to the problem at hand!

2) UNDERSTANDING THE PROBLEM:

The problem statement is simple: We need to find the Average height of a Random Binary Tree.

Intuitively, the structure of this statement, based on the input provided, output required and the computation involved is as follows:

Input: The number of nodes is the input
Output: Print the average height of all possible binary trees with the given number of nodes.
Computation Involved: Finding the average average height of all possible binary trees with the given number of nodes.

3) AVERAGE HEIGHT OF A RANDOM BINARY TREE OF 'n' NODES:

3.1) DISPOSITION:

It has been proved that the average height of a binary tree with n internal nodes is shown to be asymptotic to 2 * square root of (pi * n). This represents the average stack height of the simplest recursive tree traversal algorithm (to be discussed).

Before we discuss more, it should be emphasized that the interest of the proof is largely methodological. Almost all classical analysis of algorithms follow a chain starting with exact enumeration formula derived by direct counting arguments continued by real approximations. Let us state the theorem and modify it as we go:

Theorem:
The average height of binary trees with n internal nodes satisfies

3.2) TREE TRAVERSAL ALGORITHM

Let us limit ourselves here to a short algorithmic discussion of tree traversal. Perhaps one of the simplest recursive algorithms is the algorithm for traversing or exploring-nodes of a planar tree. Loosely described, this simple algorithm looks like this:

procedure VISIT( T: binary-tree)
    --- Operations performed---
    for U subtree-of-root-of T do
        VISIT(U)
    end loop
end procedure

Why is this algorithm important?

The focus here, is on the behavior of the tree exploration procedures in such
contexts. Analyzing the running time-complexity of the VISIT procedure is not difficult since the complexity is clearly linear in the size of the input tree.

The main problem is to evaluate the auxiliary space, i.e., to determine the average stack size (equivalently recursion depth) required for exploring a binary-tree, as a function of the size of the tree.

It can be seen that the stack size required by the visit algorithm is equal to the height of the tree. Average case analysis of the algorithm applied to a family F of input trees thus reduces to determining average heights of trees in F.

Other applications of this algorithm:

The applications of this algorithm is plentiful and frequently occurs in a number of contexts in-

• compiling
• program transformation
• term rewriting systems
• optimization and other related areas.

Theorem:
The recursive traversal procedure applied to binary trees of size n
has average storage complexity

3.3) GENERATING FUNCTIONS:

As explained in the disposition, we will be starting with the general tree enumeration formula derived by direct counting arguments to move onto our problem of binary trees.

Tree enumeration: Our approach is entirely based on generating functions. The class Y of binary (nonplane unlabelled rooted) trees is defined to include the tree with a single external node. A tree has size n if it has n external nodes (hence n − 1 internal nodes). The cardinality of the subclass Yn of trees of size n is denoted by yn and the generating function (GF) of Y is

Since we are talking about binary trees henceforth, yn will be represented as Bn. Since a binary tree is either an external node or a root appended to an unordered pair of two (not necessarily distinct) binary trees, one has the basic functional equation:

z and n are used inter-changeably to show that the terms are a function of a variable.

An alternative proof to arrive at the equation is as follows:

Let us first introduce the generating functions relative to the above function for binary trees:

• Bn - Generating function of binary tree
• Bn [h] - moment of generating function of node z binary tree of internal nodes n wrt h
• Hz - moment of Height of node z in binary tree of internal nodes n wrt h

These terms are connected and defined as:

Similar to our formula with general trees, The inductive definition of binary trees shows that the Bn, satisfy the recurrence

Solving the equation, we get:

The formula is an extension of an important series- the Catalan Series where the nth term is defined as:

The first Catalan numbers for n = 0, 1, 2, 3, ... are : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, ...

3.4) GENERAL FORMULA FOR ALL TREES:

Now that we have all the required pre-requisites for the formula:

• Hn' = the average height of all trees of size n
• Hn = height of individual binary tree
• Bn = Generating function of binary tree

Let us construct the formula:

The following table shows the distribution of height in trees of size<=7.

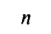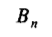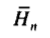1	1	2.0
2	2	3.0
3	5	3.8
4	14	4.57
5	42	5.24
6	132	5.88
7	429	6.47

Why is a general formula for trees required?

As explained in the disposition, we will be starting with the general trees formula derived by direct counting arguments to move onto our problem of binary trees. It is important to note that from here on we restrict the formula under certain constraints such that we cover just the binary trees which is a subset under the general trees bracket!

3.5) ESTIMATION TOWARDS CONSTRAINING THE GENERAL FORMULA TO BINARY TREES

We proceed to evaluate the Taylor coefficient H, of H(z) by means of
Cauchy’s integral formula selecting a contour inside that region which gives predominance to the behavior of the function around the singularity point of 1/4 (proof not discussed in this article)

To estimate the coefficients of H(z), we next translate the approximation of H(z)
into an approximation of its coefficients. Since the result is of independent interest, we state it in a slightly more general form than strictly necessary here. Solving the equation is a complex and tedious task and it does not come under the scope of this article. Let us just look at the final result.

The average height of binary trees with n internal nodes satisfies

Any improvement in the expansion of H(z) will lead
to a better error term. Numerical results corresponding to the are displayed in the table below.Notice that the convergence of Hn, to 2* root of (pi * n) is initially quite slow; however, for sizes of trees about 16000, the gap appears to be less than 2%.

The table shows: The Average Height of Binary Trees - comparing the Exact values to the Asymptotic estimates

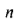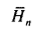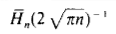10	7.07	0.631
20	11.29	0.712
50	19.98	0.797
100	29.98	0.846
200	44.29	0.883
500	72.94	0.920
1000	105.42	0.940
2000	151.50	0.956
5000	243.17	0.970
10000	346.64	0.978
16000	440.32	0.982

Thus our disposition stands: the average height of a binary tree with n internal nodes is shown to be asymptotic to 2 * square root of (pi * n).

3.6) ALGORITHM

• Read the number of nodes as in_nodes
• The number of internal nodes are n = in_nodes-1
• Find the nth catalan number as per the conditions laid earlier and assign it to Bn.
• Initialize Hn to 0.0
• In a loop from 1 to n do
  • Hn = Hn + i * (Bn^i - Bn^(i-1))
• Hn' = Hn / Bn
• Initialize asy = 2 * root_of (pi * n)
• Print results

3.7) Implementation

C++ code:

#include <iostream>
#include <cmath>
using namespace std;

int catalan(int n){
    int res=1;
    for(int i=2;i<=n;i++){
        res*=( (i+n)/i );
    }
    return res;
    
}

/*
double Hn(int n){
    int Bn=catalan(n);
    double avg=0;
    //Average(H') can be calculated here
    return avg;
} 
*/

double asymptote(int n){
    return (2*sqrt(3.14*n));
}

int main(){
    int n=15;
    printf("The average height is asymptotic to %.2f",asymptote(n));
    return 0;
}

Output:
The average height is asymptotic to 0.69

3.8) TIME-COMPLEXITY ANALYSIS

• Finding the nth catalan number takes linear time
• FInding avg linear time
• Finding the asymptotic value corresponding to avg takes constant time
• The above functions are independent of each other

Thus the time complexity is O(n+n+1) =

• Worst case time complexity: Θ(n)
• Average case time complexity: Θ(n)
• Best case time complexity: Θ(n)

3.9) SPACE-COMPLEXITY ANALYSIS

We do not use any auxiliary space in this algorithm. However, the recursive stack holds the all n nodes. Hence, the Space complexity is Θ(n)

4) SUMMARY

As we have already seen,

provided Bn <> 0. We proceed by proving that B(z) has algebraic singularities on its
circle of convergence, and that H(z) has corresponding logarithmic singularities.
We have to distinguish two cases based on the value of d = GCD {r: cr <> 0 } where r is the root node under inspection and cr denotes the branching children nodes of the root.

The situation where d is not equal to 1 for binary trees and t-ary trees requires combining results relative to each of the d singularities of y on its circle of convergence; in that case, B = 0 if n <> 1 (mod d). The solution involves
2 cases:

• Unicity of singularity(single singular point where roots of equation become undefined)
• Multiple singularities (multiple points where roots of equation become undefined)

The detailed analysis of these two cases is not in the scope of this article. However both the cases end with the equivalent result of:

Thus, we reach the point where we can state that:

THEOREM:
For simple families of trees corresponding to the equation B = z(theta) (y), and for n = 1 (mod d) with d = GCD( r: cr <> 0}, the average heights
satisfy:

The graphical representation of the theorem is:

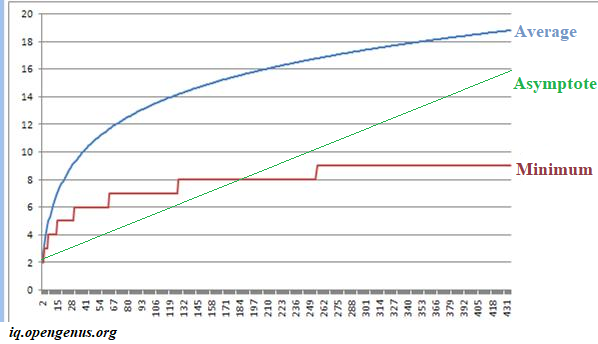
where average height is found manually and the asymptote follows the formula of the theorem.

COROLLARY:

• The average height of a unary-binary tree with n nodes is asymptotic to
  

• The average height of an unbalanced 2-3 tree with n nodes is asymptotic to
  

• The average height of a t-ary tree with n internal (t-ary) nodes is asymptotic to
  

• The average height of a (planar rooted) tree with n nodes is asymptotic to
  

• The average height of a labeled nonplanar tree with n nodes is asymptotic to
  

• And most importantly the average height of a binary-tree with n nodes is asymptotic to
  

With this article at OpenGenus, you now know how to find the average height of a random binary tree!