
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | coding time: 10 minutes
The problem we will solve is that given a set of integers in sorted order, find length of longest arithmetic progression in that set. This can be solved by brute force in O(N^3) while a dynamic programming approach with take O(N^2) time complexity.
Arithmetic progression is set of numbers in which difference between two consecutive numbers is constant. Mathematical formula for arithmetic progression is
Tn = a + (n – 1) d where a is first element, T(n) is nth element and d is constant.
1,2,3 is AP with d = 1
3,7,11,15 is AP with d = 4
Let’s define in detail first. Our Problem statement is to find longest sequence of indices, 0 < i1 < i2 < … < ik < n such that sequence A[i1], A[i2], …, A[ik] is an arithmetic progression.
Examples:
set[] = {1, 7, 10, 15, 27, 29}
output = 3
The longest arithmetic progression is {1, 15, 29}
set[] = {5, 10, 15, 20, 25, 30}
output = 6
The longest arithmetic progression is {5, 10, 15, 20, 25, 30}
What will be the brute force solution?
A brute force solution is to one by one consider every pair as first two elements of AP and check for the remaining elements in sorted set. To consider all pairs as first two elements, we need to run a O(n^2) nested loop. Inside the nested loops, we need a third loop which linearly looks for the more elements in Arithmetic Progression (AP). This process takes O(n3) time.
For better understanding Lets us go through an example:-
Let us consider a sorted array and we have to find 3 or more elements in AP. if we get 3 elements in AP we return TRUE otherwise FALSE.
In order to find three elements, we first fix an element as middle element and search for other two (one smaller and one greater). We start from the second element and fix every element as middle element. For an element set[j] to be middle of AP, there must exist elements ‘set[i]’ and ‘set[k]’ such that set[i] + set[k] = 2*set[j] where 0 <= i < j and j < k <=n-1.
We can follow this ALGO to find numbers:-
Initialize i as j-1 and k as j+1
Do following while i >= 0 and j <= n-1
If set[i] + set[k] is equal to 2*set[j], then we are done.
If set[i] + set[k] > 2*set[j], then decrement i (do i–).
Else if set[i] + set[k] < 2*set[j], then increment k (do k++).
This will give answer to question if there exist three numbers in set which form AP.
If set contains two or more elements,** minimum length** of longest AP will be2. Why? because any number will always form AP of length 2 with last element of set.
We can proceed with this problem using Dynamic Programming
The idea is to create a 2D table L[n][n]. An entry L[i][j] in this table stores Longest arithmatic progression with arr[i] and arr[j] as first two elements of AP and (j > i). The last column of the table is always 2 (as discussed above). Rest of the table is filled from bottom right to top left. To fill rest of the table, j (second element in AP) is first fixed. i and k are searched for a fixed j. If i and k are found such that i, j, k form an AP, then the value of L[i][j] is set as L[j][k] + 1. Note that the value of L[j][k] must have been filled before as the loop traverses from right to left columns.
Algorithm to find length of longest arithmetic progression
- For j = n L[i][j] = 2 for 0<i<n, bottom most column filled with 2.
- Fix j = n-1 to 1 and for each j do below steps:
- Find all i and k such that A[i], A[j] and A[k] form AP. Algorithm given above.
- Fill L[i][j] = 1 + L[j][k]
- Check if L[i][j] is longer than current max length, if yes, update it.
- Slight change for optimization, if A[i] + A[k] is greater than 2*A[j], we can safely fill L[i][j] as 2.
- While i > 0 even after k > n, fill all L[i][j] =2.
Example
Let us consider the example number 1 where input array was a[]={ 1, 3, 5, 6, 8, 7 }.
Now when we will build the dp[n][n] matrix it would look like following-
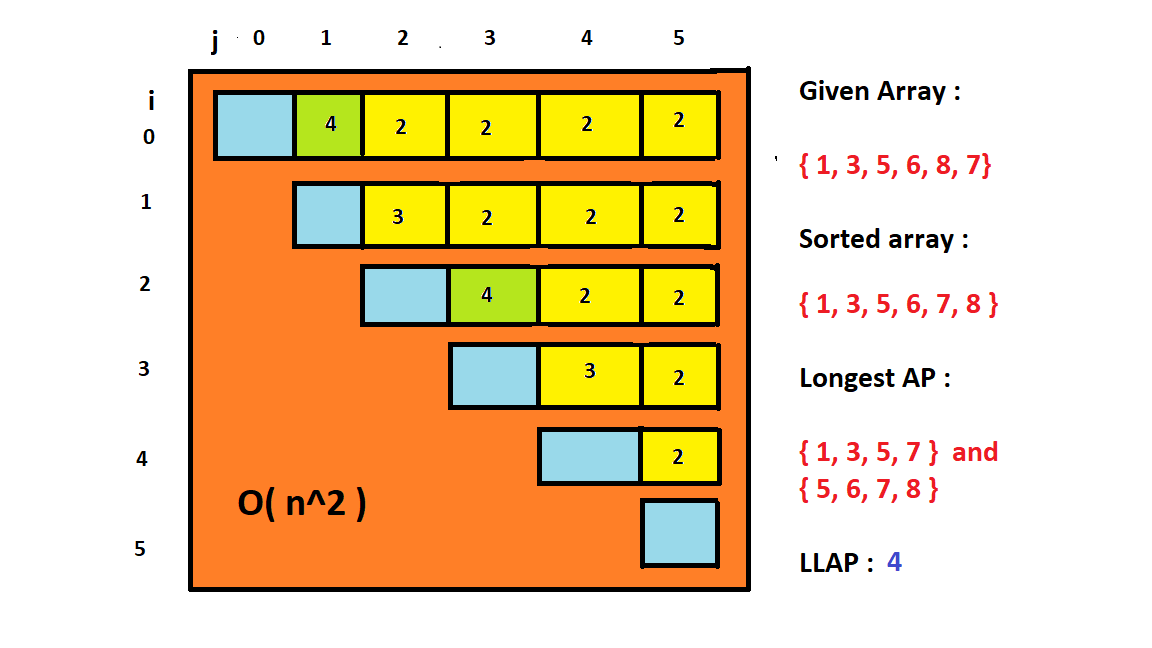
From the above method we can see that we will be using only n-1 + ...... + 3 + 2 + 1 space of the matrix making the time complexity to be n*(n-1)/2 ~ O(n^2).
Complexity
Time Complexity: O(n^2) [Dynamic programming]
Auxiliary Space: O(n^2)
Implementations
#include <iostream>
using namespace std;
// Returns length of the longest AP subset in a given set
int lenghtOfLongestAP(int set[], int n)
{
if (n <= 2) return n;
// Create a table and initialize all values as 2. The value of
// L[i][j] stores LLAP with set[i] and set[j] as first two
// elements of AP. Only valid entries are the entries where j>i
int L[n][n];
int llap = 2; // Initialize the result
// Fill entries in last column as 2. There will always be
// two elements in AP with last number of set as second
// element in AP
for (int i = 0; i < n; i++)
L[i][n-1] = 2;
// Consider every element as second element of AP
for (int j=n-2; j>=1; j--)
{
// Search for i and k for j
int i = j-1, k = j+1;
while (i >= 0 && k <= n-1)
{
if (set[i] + set[k] < 2*set[j])
k++;
// Before changing i, set L[i][j] as 2
else if (set[i] + set[k] > 2*set[j])
{ L[i][j] = 2, i--; }
else
{
// Found i and k for j, LLAP with i and j as first two
// elements is equal to LLAP with j and k as first two
// elements plus 1. L[j][k] must have been filled
// before as we run the loop from right side
L[i][j] = L[j][k] + 1;
// Update overall LLAP, if needed
llap = max(llap, L[i][j]);
// Change i and k to fill more L[i][j] values for
// current j
i--; k++;
}
}
// If the loop was stopped due to k becoming more than
// n-1, set the remaining entties in column j as 2
while (i >= 0)
{
L[i][j] = 2;
i--;
}
}
return llap;
}
int main()
{
int set1[] = {1, 7, 10, 13, 14, 19};
int n1 = sizeof(set1)/sizeof(set1[0]);
cout << lenghtOfLongestAP(set1, n1) << endl;
return 0;
}
Output:
4
