Longest Common Prefix

In this article, we are going to explore different approaches to find the longest common prefix between two strings. Same techniques can be applied to find the Longest Common Prefix for multiple strings.

Table of Content

1. Examining the Problem Statement
2. Different Approaches to Solving the Problem
   1. The iterative character matching approach
   2. The Trie approach
3. Conclusion

Examining the Problem Statement

Before we start solving any problem we have to understand what the problem statement entails. Having a thorough understanding of a problem is the first step in being able to solve it. It helps if we restate our problem definition in a more explicit way to make it more obvious what our inputs and outputs are.

Given two strings as input return the longest common prefix between them if it exists else return an empty string assuming that both strings are all in lowercase.

We now clearly see the inputs and output, to fully grok the problem, we need to define what a prefix is. A prefix is a contiguous sequence of characters that occur at the beginning of a string. The null string and the full string itself can also be the prefix of a string.

We now have a better understanding of the problem statement so we can proceed to implement a solution.

Different Approaches to Solving the Problem

The iterative character matching approach

This entails gradually building up our prefix string by iteratively comparing the next substring of both strings until they no longer match or the smaller string is exhausted. Let's use an example to truly see what we mean by the above statement.
Given the strings study and studious, find the longest common prefix. Now what we mean by iteratively comparing the next/successive substring is that starting from the smallest substrings of both study and studious we compare them to see if they are the same. In this case that is "s", since both are equal we move to the next index and compare both substrings again. Now we have the substring "st" since both strings share this substring we move on to the next iteration (When we make our comparisons we only need to check if the newest characters added to the substrings are equal). The next substring is "stu" and then "stud". We then check the next iteration. Here we have "study" and "studi" since i != y then the substring of both strings no longer match we end our iteration and return substring we have gathered just before the terminating iteration which is "stud".

The Implementation

def longestCommonPrefix(word1, word2):
    # ensure that word1 always holds the string with the smaller size
    word1, word2 = (word1, word2) if min(word1, word2) == word1 else (word2, word1)
    prefix = ""
    for i in range(len(word1)):
        if word1[i] !=  word2[i]:
            return prefix
        prefix += word1[i]
    
    return prefix

Time Complexity

The above algorithm has a time complexity of O(n) where n is the length of the smaller string and has a space complexity of O(n). Although we could make the space complexity O(1) by modifying the code. I shall leave it as an exercise for the reader to see how to achieve this

The Trie approach

Here, we shall utilise a data structure called a trie to get the longest common prefix. A trie is a search tree data structure often also referred to as a prefix-tree because of the way it operates as we will come to see. In short terms, a trie is a tree where every node has a maximum of all the letters of the alphabet as children. We populate a trie by moving down it and marking the nodes that correspond to the letters of the word

An Illustration of how a trie operates by adding the words look, loop and rake into it

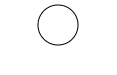
An Empty trie starts with just the root node

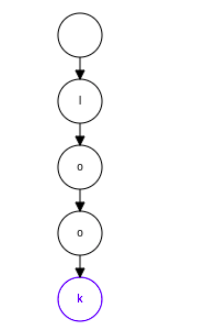
First, we insert the word look, after inserting every letter we insert the next one as its child downwards the tree until we exhaust the word

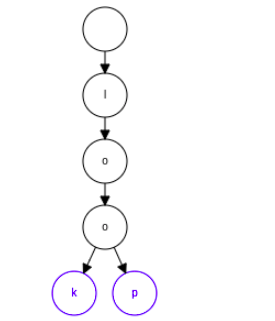
then insert the word loop, now as can be seen we reuse nodes if they already exist only adding a new node downwards if there is a divergence.

finally, we insert the word rake. Here since there is no common words at all a new path diverges immediately from the root

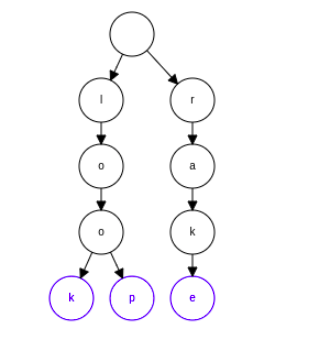
Using the trie we were able to represent those three words. Tries are useful data structures and have a lot of applications

Using the trie to solve the problem

The trie is called a prefix tree and our problem has to do with getting a common prefix so even at first glance we might see that a trie might be able to solve this problem. A trie solves the problem very well it would work not only in this case but in the general case of the problem where we had more than 2 strings in which we wanted to find the common prefix.

To solve the problem we populate the trie with the two strings, then we traverse the trie to see the point where the strings branch off. The point branching off signifies that the two words no longer share the same characters hence the character path just before branching is the common prefix between the two words

The Implementation

class Trie:
  def __init__(self):
    self.isleaf = False
    self.children = {}

  def insert(self, word):
    """ insert a full word into the Trie by traversing it fully adding 
    new nodes if they do not already exist """
    
    currentnode = self
    for char in word:
      if currentnode.children.get(char, None) is None:
        currentnode.children[char] = Trie()
      
      currentnode = currentnode.children[char]
    currentnode.isleaf = True

def longestCommonPrefix(word1, word2):
  # first add the words to the trie
  trie = Trie()
  trie.insert(word1)
  trie.insert(word2)

  prefixstring = ""
  node = trie

  # traverse the tree until you find the branch point then return the prefix string just before then
  while node:
    # if we have more than one child then a split has occurred
    children = list(node.children.keys())
    if not node.isleaf and len(children) == 1:
      char = children[0]
      prefixstring += char
      node = node.children[char]
    else:
      return prefixstring

Time Complexity

The above implementation has a time complexity O(n) where n is the number of characters.

Conclusion

We have been able to look at 2 approaches to solving the problem of the common prefix between two strings. We looked at the relative intuitive iterative approach and we also looked at approaching the problem with a data structure, the trie.

With this article at OpenGenus, you must have the complete idea of Longest Common Prefix.