Reading time: 50 minutes | Coding time: 60 minutes

In this article, we have explored an insightful approach/ algorithm to find the 4 elements in an array whose sum is equal to the required answer (4 Sum problem). This concept finds many uses in computational geometry.

CONTENTS OF THE ARTICLE:

• Problem Statement Definition
• Method 1: Naive approach
• Method 2: Sorting for efficiency
• Method 3: Auxiliary Space approach
• Method 4: Hashing Based Solution (1)
• Method 5: Hashing Based Solution (2)
• Method 6: Hashing Based Solution (3)
• Applications

PROBLEM STATEMENT DEFINITION

Given an array nums of n integers and an integer target, are there elements a, b, c, and d in nums such that a + b + c + d = target we need to find all unique quadruplets in the array which gives the sum of target.

Note: The solution set must not contain duplicate quadruplets.

Example-1

Input: nums = [1,0,-1,0,-2,2],
target = 0

Output: [[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

Explanation:
Sum of outputs is equal to 0,
i.e. -2 + -1 + 1 + 2 = 0, -2 + 0 + 0 + 2 = 0, -1 + 0 + 0 + 1 = 0

Example-2

Input: nums = {10, 2, 3, 4, 5, 9, 7, 8}
target = 23
Output: [3, 5, 7, 8]

Explanation:
Sum of output is equal to 23,
i.e. 3 + 5 + 7 + 8 = 23.

There are three methods for solving the closest 3 sum problem

Method 1: Naive approach
Method 2: Using Python Bisect
Method 3: Sorting and Two Pointer Approach
Let us look at all three methods.

METHOD-1 NAIVE APPROACH

A Naive Solution is to generate all possible quadruples and compare the sum of every quadruple with X. The following code implements this simple method using four nested loops

ALGORITHM

• Given an array of length n and a sum s
• Create four nested loop first loop runs from start to end (loop counter i), second loop runs from i+1 to end (loop counter j), third loop runs from j+1 to end (loop counter k), fourth loop runs from k+1 to end (loop counter l)
• The counter of these loops represents the index of 4 elements of the triplets.
• Find the sum of ith, jth, kth and lth element and compare it with sum (s)
• If it is equal, print the quadruple set and check for other solution sets

IMPLEMENTATION

Let us have a look at the C++ program for the problem

#include <bits/stdc++.h>
using namespace std; 

void Naive_4SUM(int A[], int n, int S)
{
     
// Select the first element and find other three
for (int i = 0; i < n - 3; i++)
{
    // Select the second element and find other two
    for (int j = i + 1; j < n - 2; j++)
    {
         
        // Select the third element and find the fourth
        for (int k = j + 1; k < n - 1; k++)
        {
            // Find the fourth element
            for (int l = k + 1; l < n; l++)
            if (A[i] + A[j] + A[k] + A[l] == S) //Comparing the sum with S
                cout << "["<<A[i] <<", " << A[j]<< ", " << A[k] << ", " << A[l]<<"]"<<endl;
        }
    }
}
}
 

int main()
{
    int nums[] = {10, 2, 3, 4, 5, 9, 7, 8} ;
    int n = sizeof(nums) / sizeof(nums[0]);
    int target = 23;
    Naive_4SUM(nums, n, target);
    return 0;
}

Output:
[3, 5, 7, 8]

Complexity

• Worst case time complexity: Θ(n^4)
• Average case time complexity: Θ(n^4)
• Best case time complexity: Θ(n^4)
• Space complexity: Θ(1)

METHOD-2 SORTING FOR EFFICIENCY

The time complexity of the above algorithm can be improved to O(n^3) with the use of sorting as a preprocessing step, and then using method 1 of this article to reduce one loop implementation.

ALGORITHM

• Sort the array in time O(n * log n).
• Now for each element i and j, do the following steps —
• Set two pointers left — k = j + 1 and right — l = n - 1.
• Check if nums[i] + nums[j] + nums[k] + nums[l] == target and add it to the result, if true/
• If nums[i] + nums[j] + nums[k] + nums[l] < target, then we are too left, and we need to move right so increment left pointer i.e. k++.
• If nums[i] + nums[j] + nums[k] + nums[l] > target, then we are too right, and we need to decrement the right pointer i.e., l--.

IMPLEMENTATION

1. Python Function for the same algorithm

def fourSum(nums: List[int], target: int) -> List[List[int]]:
    # Resultant list
    quadruplets = list()
    # Base condition
    if nums is None or len(nums) < 4:
        return quadruplets
    # Sort the array
    nums.sort()
    # Length of the array
    n = len(nums)
    # Loop for each element of the array
    for i in range(0, n - 3):
        # Check for skipping duplicates
        if i > 0 and nums[i] == nums[i - 1]:
            continue
        # Reducing to three sum problem
        for j in range(i + 1, n - 2):
            # Check for skipping duplicates
            if j != i + 1 and nums[j] == nums[j - 1]:
                continue
            # Left and right pointers
            k = j + 1
            l = n - 1
            # Reducing to two sum problem
            while k < l:
                current_sum = nums[i] + nums[j] + nums[k] + nums[l]
                if current_sum < target:
                    k += 1
                elif current_sum > target:
                    l -= 1
                else:
                    quadruplets.append([nums[i], nums[j], nums[k], nums[l]])
                    k += 1
                    l -= 1
                    while k < l and nums[k] == nums[k - 1]:
                        k += 1
                    while k < l and nums[l] == nums[l + 1]:
                        l -= 1
    return quadruplets

2. JAVA Function for the same algorithm

public class FourSum {

    private static List<List<Integer>> fourSum(int[] nums, int target) {
        // Resultant list
        List<List<Integer>> quadruplets = new ArrayList<>();
        // Base condition
        if (nums == null || nums.length < 4) {
            return quadruplets;
        }
        // Sort the array
        Arrays.sort(nums);
        // Length of the array
        int n = nums.length;
        // Loop for each element in the array
        for (int i = 0; i < n - 3; i++) {
            // Check for skipping duplicates
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            // Reducing problem to 3Sum problem
            for (int j = i + 1; j < n - 2; j++) {
                // Check for skipping duplicates
                if (j != i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }
                // Left and right pointers
                int k = j + 1;
                int l = n - 1;
                // Reducing to two sum problem
                while (k < l) {
                    int currentSum = nums[i] + nums[j] + nums[k] + nums[l];
                    if (currentSum < target) {
                        k++;
                    } else if (currentSum > target) {
                        l--;
                    } else {
                        quadruplets.add(Arrays.asList(nums[i], nums[j], nums[k], nums[l]));
                        k++;
                        l--;
                        // Check for skipping duplicates
                        while (k < l && nums[k] == nums[k - 1]) {
                            k++;
                        }
                        while (k < l && nums[l] == nums[l + 1]) {
                            l--;
                        }
                    }
                }
            }
        }
        return quadruplets;
    }
}

3. Let us have a look at the C++ program for the problem

#include<bits/stdc++.h>
using namespace std;
 
void SORT_4SUM(int nums[], int n, int X)
{
    int l, r;
    
    //Using library function sort
    sort(nums, nums+n);
 
    
    for (int i = 0; i < n - 3; i++)
    {
        for (int j = i+1; j < n - 2; j++)
        {
            // Initialize two variables as indexes of the first and last elements in the remaining elements
            l = j + 1;
            r = n-1;
 
            
            while (l < r)
            {
                if( nums[i] + nums[j] + nums[l] + nums[r] == X)
                {
                    cout <<"["<< nums[i]<<", " << nums[j] <<
                        ", " << nums[l] << ", " << nums[r]<<"]"<<endl;
                    l++; r--;
                }
                else if (nums[i] + nums[j] + nums[l] + nums[r] < X)
                    l++;
                else // nums[i] + nums[j] + nums[l] + nums[r] > X
                    r--;
            } 
        } 
    } 
 

int main()
{
    int nums[] = {10, 2, 3, 4, 5, 9, 7, 8} ;
    int n = sizeof(nums) / sizeof(nums[0]);
    int target = 23;
    SORT_4SUM(nums, n, target);
    return 0;
}

Output:
[3, 5, 7, 8]

Time-Complexity analysis

We are scanning the entire array keeping one element fixed and then doing it for another element fixed. We are doing this for every element in the array. Thus, we are scanning each element of array n number of times. And we are doing this for n times, hence the worst case time complexity will be O(n3 + n * log n) which comes down to O(n3). Hence we can write the worst-case, average-case and best-case time complexities as

• Worst case time complexity: Θ(n^3)
• Average case time complexity: Θ(n^3)
• Best case time complexity: Θ(n^3)

Space-Complexity analysis

We are not using any data structure for the intermediate computations, hence the space complexity is O(1).

• Space complexity: Θ(n)

METHOD-3 AUXILARY SPACE APPROACH

Auxiliary Space is the extra space or temporary space used by an algorithm. TThis problem can also be solved in O(n^2 * logn) time with the help of auxiliary space.

APPROACH EXPLANATION

Create an auxiliary array temp[] of size n*(n-1)/2 where n is the size of nums[]
Store sum of all possible pairs in temp[].
Sort the auxiliary array temp[].
Now the problem reduces to find two elements in temp[] with sum equal to X. We can use the naive method (method-1) of this article to find the two elements efficiently.

NOTE:

An element in temp[] represents a pair from nums[].
While picking two elements from temp[], we must check whether the two elements have an element of nums[] in common.
For example, if first element of temp[] is the sum of nums[1] and nums[2], and second element of temp[] is the sum of nums[2] and nums[4], then these two elements of temp[] do not represent four distinct elements of input array nums[].

DRAWBACK OF THIS APPROACH

The big size of the auxiliary array can be a concern in this method.

IMPLEMENTATION

Let us have a look at the C program for the problem

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

struct pairSum {
 
    // index (int A[]) of first element in pair
    int first;
 
    // index of second element in pair
    int sec;
 
    // sum of the pair
    int sum;
};
typedef struct pairSum pairSum;

int compare(const void* a, const void* b)
{
    return ((*(pairSum*)a).sum - (*(pairSum*)b).sum);
}
 

bool noCommon(struct pairSum a, struct pairSum b)
{
    if (a.first == b.first || a.first == b.sec
        || a.sec == b.first || a.sec == b.sec)
        return false;
    return true;
}
 

void AUX_4SUM(int arr[], int n, int X)
{
    int i, j;
 
    
    int size = (n * (n - 1)) / 2;
    struct pairSum aux[size];
 
   
    int k = 0;
    for (i = 0; i < n - 1; i++) {
        for (j = i + 1; j < n; j++) {
            aux[k].sum = arr[i] + arr[j];
            aux[k].first = i;
            aux[k].sec = j;
            k++;
        }
    }
 
   
    qsort(aux, size, sizeof(aux[0]), compare);
 

    i = 0;
    j = size - 1;
    while (i < size && j >= 0) {
        if ((aux[i].sum + aux[j].sum == X)
            && noCommon(aux[i], aux[j])) {
            printf("[%d, %d, %d, %d]\n", arr[aux[i].first],
                   arr[aux[i].sec], arr[aux[j].first],
                   arr[aux[j].sec]);
            return;
        }
        else if (aux[i].sum + aux[j].sum < X)
            i++;
        else
            j--;
    }
}
 

int main()
{
    int nums[] = { 10, 20, 30, 40, 1, 2 };
    int n = sizeof(nums) / sizeof(nums[0]);
    int target = 91;
    
    
    AUX_4SUM(nums, n, target);
    return 0;
}

Output:
[20, 1, 30, 40]

Let us look at the C++ implementation of the program

#include <bits/stdc++.h>
using namespace std;
 

class pairSum {
public:    
    int first;
    int sec;
    int sum;
};
 
bool noCommon(pairSum a, pairSum b)
{
    if (a.first == b.first || a.first == b.sec
        || a.sec == b.first || a.sec == b.sec)
        return false;
    return true;
}
 

int compare(const void* a, const void* b)
{
    return ((*(pairSum*)a).sum - (*(pairSum*)b).sum);
}

void AUX_4SUM(int arr[], int n, int X)
{
    int i, j;
 
    
    int size = (n * (n - 1)) / 2;
    pairSum aux[size];
 
   
    int k = 0;
    for (i = 0; i < n - 1; i++) {
        for (j = i + 1; j < n; j++) {
            aux[k].sum = arr[i] + arr[j];
            aux[k].first = i;
            aux[k].sec = j;
            k++;
        }
    }
 
    
    qsort(aux, size, sizeof(aux[0]), compare);
    i = 0;
    j = size - 1;
    while (i < size && j >= 0) {
        if ((aux[i].sum + aux[j].sum == X)
            && noCommon(aux[i], aux[j])) {
            cout << "["<< arr[aux[i].first] << ", " << arr[aux[i].sec] << ", "<< arr[aux[j].first] << ", "<< arr[aux[j].sec] <<"]"<< endl;
            return;
        }
        else if (aux[i].sum + aux[j].sum < X)
            i++;
        else
            j--;
    }
}
 
// Driver code
int main()
{
    int nums[] = { 10, 20, 30, 40, 1, 2 };
    int n = sizeof(nums) / sizeof(nums[0]);
    int target = 91;
    
    
    AUX_4SUM(nums, n, target);
    return 0;
}

Output:
[20, 1, 30, 40]

Time-Complexity analysis

Step-1 of the algorithm can be completed O(n^2) time. The second step is sorting an array of size O(n^2). Sorting can be done in O(n^2 * logn) time using merge sort or heap sort or any other O(n * logn) algorithm. The third step takes O(n^2) time. So overall complexity is O(n^2 * logn)

• Worst case time complexity: Θ(n^2 * logn)
• Average case time complexity: Θ(n^2 * logn)
• Best case time complexity: Θ(n^2 * logn)

Space-Complexity analysis

The size of the auxiliary array is O(n^2).

• Space complexity: Θ(n^2)

METHOD-4 HASHING BASED SOLUTION (1)

APPROACH EXPLANATION

The idea is to consider every pair of elements in the array one by one and insert it into a hash table. For each pair of elements (i,j), calculate the remaining sum. If the remaining sum exists in the map and elements involved in the previous occurrence does not overlap with the current pair, i.e, (i,j,i,y) or (i,j,x,i) or (i,j,j,y) or (i,j,x,j), print the quadruplet and return

This method is the least efficient of all hashing based methods

IMPLEMENTATION

1. Let us look at the c++ implementation

#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;
 
typedef pair<int, int> Pair; 

bool hasQuadruplet(int arr[], int n, int target)
{
    // create an empty map
    // `key` —> target of a pair in the array
    // `value` —> vector storing an index of every pair having that sum
    unordered_map<int, vector<Pair>> map;
 
    // consider each element except the last element
    for (int i = 0; i < n - 1; i++)
    {
        
        for (int j = i + 1; j < n; j++)
        {
            
            int val = target - (arr[i] + arr[j]);
 
            // if the remaining sum is found on the map,
            // we have found a quadruplet
            if (map.find(val) != map.end())
            {
                // check every pair having a sum equal to the remaining sum
                for (auto pair: map.find(val)->second)
                {
                    int x = pair.first;
                    int y = pair.second;
 
                    // if quadruplet doesn't overlap, print it and return true
                    if ((x != i && x != j) && (y != i && y != j))
                    {
                        cout << "["
                            << arr[i] << ", " << arr[j] << ", " << arr[x]
                            << ", " << arr[y] << "]";
                        return true;
                    }
                }
            }
 
            // insert the current pair into the map
            map[arr[i] + arr[j]].push_back({i, j});
        }
    }
 
    // return false if quadruplet doesn't exist
    return false;
}
 
int main()
{
    int nums[] = { 2, 7, 4, 0, 9, 5, 1, 3 };
    int target = 20;
 
    int n = sizeof(nums/ sizeof(nums[0]);
 
    if (!hasQuadruplet(nums, n, target)) {
        cout << "Quadruplet Doesn't Exist";
    }
 
    return 0;
}

OUTPUT:
[4, 0, 7, 9]

2. Let us implement the program in JAVA

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
 
class Pair
{
    public int x, y;
 
    Pair(int x, int y)
    {
        this.x = x;
        this.y = y;
    }
}
 
class Main
{
    
    public static boolean hasQuadruplet(int[] A, int n, int target)
    {
        // create an empty map
        // `key` —> target of a pair in the array
        // `value` —> list storing an index of every pair having that sum
        Map<Integer, List<Pair>> map = new HashMap<>();
 
        // consider each element except the last element
        for (int i = 0; i < n - 1; i++)
        {
            // start from the i'th element until the last element
            for (int j = i + 1; j < n; j++)
            {
                // calculate the remaining sum
                int val = target - (A[i] + A[j]);
 
                // if the remaining sum is found on the map,
                // we have found a quadruplet
                if (map.containsKey(val))
                {
                    // check every pair having a sum equal to the remaining sum
                    for (Pair pair: map.get(val))
                    {
                        int x = pair.x;
                        int y = pair.y;
 
                        // if quadruplet doesn't overlap, print it and
                        // return true
                        if ((x != i && x != j) && (y != i && y != j))
                        {
                            System.out.print("["
                                        + A[i] + ", " + A[j] + ", "
                                        + A[x] + ", " + A[y] + "]");
                            return true;
                        }
                    }
                }
 
                // insert the current pair into the map
 
                // null check (Java 8)
                map.putIfAbsent(A[i] + A[j], new ArrayList<>());
                map.get(A[i] + A[j]).add(new Pair(i, j));
            }
        }
 
        // return false if quadruplet doesn't exist
        return false;
    }
 
    public static void main(String[] args)
    {
        int[] A = { 2, 7, 4, 0, 9, 5, 1, 3 };
        int target = 20;
 
        if (!hasQuadruplet(A, A.length, target)) {
            System.out.print("Quadruplet Doesn't Exist");
        }
    }
}

OUTPUT:
[4, 0, 7, 9]

Complexity

• Worst case time complexity: Θ(n^3)
• Average case time complexity: Θ(n^3)
• Best case time complexity: Θ(n^3)
• Space complexity: Θ(n^3)

METHOD-5 HASHING BASED SOLUTION (2)

The concept is similar to the above method but this method is more efficient because it uses just 3 loops compared to the latter's 4.

ALGORITHM

• Store sums of all pairs in a hash table
• Traverse through all pairs again and search for target – (current pair sum) in the hash table.
• If a pair is found with the required sum, then make sure that all elements are distinct array elements and an element is not considered more than once.

IMPLEMENTATION

#include <bits/stdc++.h>
using namespace std;
 

void HASH_4SUM(int arr[], int n, int X)
{
    // Store sums of all pairs in a hash table
    unordered_map<int, pair<int, int> > mp;
    for (int i = 0; i < n - 1; i++)
        for (int j = i + 1; j < n; j++)
            mp[arr[i] + arr[j]] = { i, j };
 
    
    for (int i = 0; i < n - 1; i++) {
        for (int j = i + 1; j < n; j++) {
            int sum = arr[i] + arr[j];
 
            // If X - sum is present in hash table,
            if (mp.find(X - sum) != mp.end()) {
                pair<int, int> p = mp[X - sum];
                if (p.first != i && p.first != j
                    && p.second != i && p.second != j) {
                    cout <<"["<< arr[i] << ", " << arr[j] << ", "<< arr[p.first] << ", "<< arr[p.second]<<"]";
                    return;
                }
            }
        }
    }
}
 

int main()
{
    int nums[] = { 10, 20, 30, 40, 1, 2 };
    int n = sizeof(nums) / sizeof(nums[0]);
    int target = 91;
    HASH_4SUM(nums, n, target);
    return 0;
}

OUTPUT
[20, 30, 40,1]

COMPLEXITY

Nested traversal is needed to store all pairs in the hash Map.

• Worst case time complexity: Θ(n^2)
• Average case time complexity: Θ(n^2)
• Best case time complexity: Θ(n^2)

All n*(n-1) pairs are stored in hash Map so the space required is O(n^2)

• Space complexity: Θ(n^2)

METHOD-6 HASHING BASED SOLUTION (3)

The issue with the approach mentioned previously and such similar algorithms is that we get non-unique quadruple values or multiple non-unique quadruples. In other words, we might get two distinct pairs but the elements in them may not be unique. Let us see an example to understand the statement.

VISUAL EXAMPLE

Let us consider an array and target

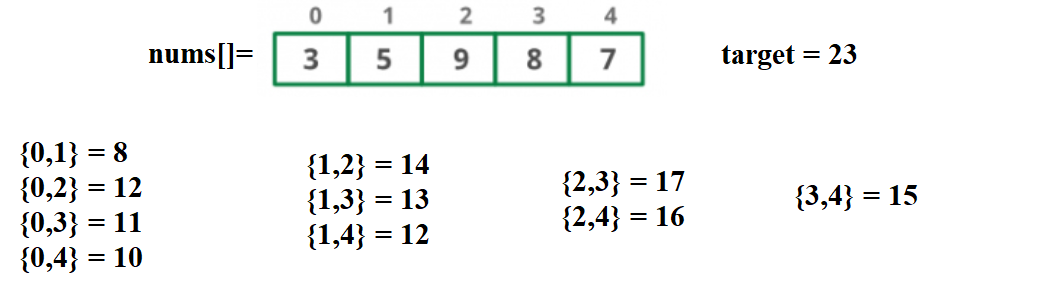
As you can see, we have all pairs of elements and their sums. We start with the first pair ({0,1}) and check if we find 23-8= 15 in the hash table

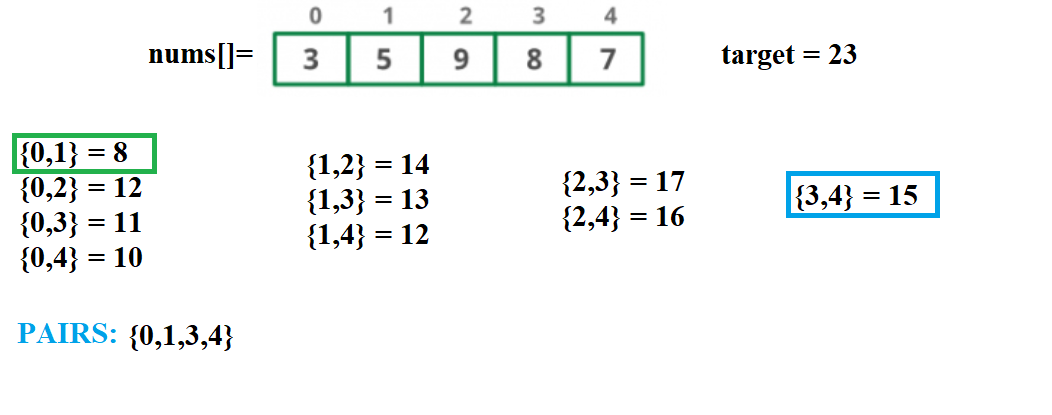
We find a pair {3,4} whose sum = 15. The four elements found are all distinct. Hence we add the four elements to the solution quadruple.

Next we move to {0,2}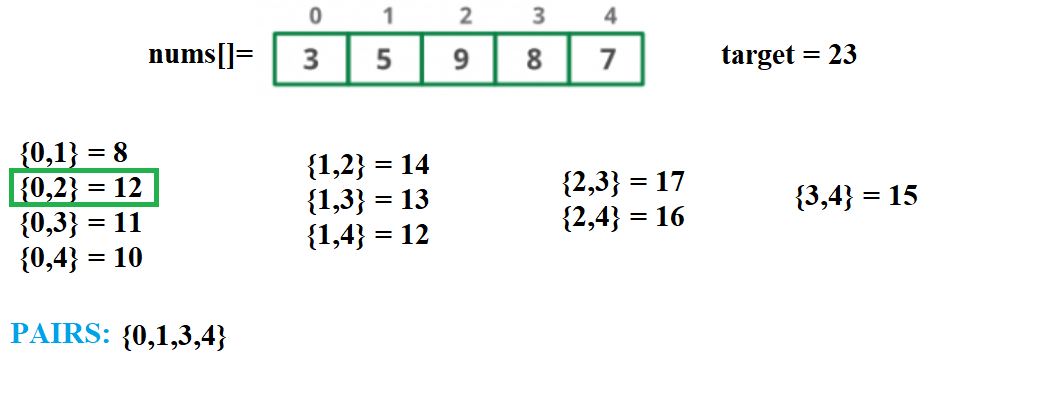

Although 23-12=11 is found in the hash table, the element 0 is repeated. So we do not add this to the solution quadruple.

Next we move to the pair {0,3}
Its complement pair is {1,4} but we cannot include it as we already have the same unordered quadruple.
Following the same procedure for all hash pairs, gives the unique quadruples whose sum is equal to 23.

DRAWBACK OF THIS APPROACH

The big size of the auxiliary array can be a concern in this method.

ALGORITHM

The algorithm is the same as the previous one with one change. we consider yet another auxiliary array ( temp[n] ) which tells us if the element under inspection is already a part of a solution quadruple

• Store sums of all pairs in a hash table
• Traverse through all pairs again and search for target – (current pair sum) in the hash table.
• Consider a temp array that is initially stored with 0. It is changed to 1 when we get 4 elements that sum up to the required value.
• If a pair is found with the required sum, then make sure that all elements are distinct array elements and check if the value in temp array is 0 so that duplicates are not considered.

IMPLEMENTATION

1. Let us consider the C implementation

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
 

struct pairSum {
 
    
    int first;
    int sec;
    int sum;
};
typedef struct pairSum pairSum;

int compare(const void* a, const void* b)
{
    return ((*(pairSum*)a).sum - (*(pairSum*)b).sum);
}
 
bool noCommon(struct pairSum a, struct pairSum b)
{
    if (a.first == b.first || a.first == b.sec
        || a.sec == b.first || a.sec == b.sec)
        return false;
    return true;
}


void HASH_4SUM(int arr[], int n, int X)
{
    int i, j;
    int size = (n * (n - 1)) / 2;
    struct pairSum aux[size];
    int k = 0;
    for (i = 0; i < n - 1; i++) {
        for (j = i + 1; j < n; j++) {
            aux[k].sum = arr[i] + arr[j];
            aux[k].first = i;
            aux[k].sec = j;
            k++;
        }
    }
 
    
    qsort(aux, size, sizeof(aux[0]), compare);//sorting the array
    i = 0;
    j = size - 1;
    while (i < size && j >= 0) {
        if ((aux[i].sum + aux[j].sum == X)
            && noCommon(aux[i], aux[j])) {
            printf("[%d, %d, %d, %d]\n", arr[aux[i].first],arr[aux[i].sec], arr[aux[j].first],arr[aux[j].sec]);
            return;
        }
        else if (aux[i].sum + aux[j].sum < X)
            i++;
        else
            j--;
    }
}
 
int main()
{
    int nums[] = { 10, 20, 30, 40, 1, 2 };
    int n = sizeof(nums) / sizeof(nums[0]);
    int target = 91;
    
    
    HASH_4SUM(nums, n, target);
    return 0;
}

OUTPUT
[20, 30, 40,1]

2. Let us consider the C++ implementation

#include <bits/stdc++.h>
using namespace std;

class pairSum {
public:
    int first;
    int sec;
    int sum;
};

int compare(const void* a, const void* b)
{
    return ((*(pairSum*)a).sum - (*(pairSum*)b).sum);
}
 

bool noCommon(pairSum a, pairSum b)
{
    if (a.first == b.first || a.first == b.sec
        || a.sec == b.first || a.sec == b.sec)
        return false;
    return true;
}
 

void HASH_4SUM(int arr[], int n, int X)
{
    int i, j;
    int size = (n * (n - 1)) / 2;
    pairSum aux[size];
    int k = 0;
    for (i = 0; i < n - 1; i++) {
        for (j = i + 1; j < n; j++) {
            aux[k].sum = arr[i] + arr[j];
            aux[k].first = i;
            aux[k].sec = j;
            k++;
        }
    }
 
    qsort(aux, size, sizeof(aux[0]), compare);
 
    
    j = size - 1;
    while (i < size && j >= 0) {
        if ((aux[i].sum + aux[j].sum == X)
            && noCommon(aux[i], aux[j])) {
            cout << "[" << arr[aux[i].first] << ", " << arr[aux[i].sec] << ", " << arr[aux[j].first] << ", " << arr[aux[j].sec] << "]" <<endl;
            return;
        }
        else if (aux[i].sum + aux[j].sum < X)
            i++;
        else
            j--;
    }
}
 

int main()
{
    int nums[] = {10, 2, 3, 4, 5, 9, 7, 8} ;
    int n = sizeof(nums) / sizeof(nums[0]);
    int target = 23;
    HASH_4SUM(nums, n, target);
    return 0;
}

OUTPUT:
[2, 8, 4, 9]

Time-Complexity Analysis

The first step in the algorithm takes O(n^2) time. The second step is sorting an array of size O(n^2). Sorting can be done in O(n^2 * logn) time using merge sort or heap sort or any other O(n * logn) algorithm. The third step takes O(n^2) time. So overall complexity is O(n^2 * logn).

• Worst case time complexity: Θ(n^2 * logn)
• Average case time complexity: Θ(n^2 * logn)
• Best case time complexity: Θ(n^2 * logn)

Space-Complexity Analysis

The size of the auxiliary array is O(n^2).

• Space complexity: Θ(n^2)

APPLICATIONS OF 4 SUM PROBLEM

• This problem is the most basic of a class of algorithms developed by Howgrave-Graham and Joux
• A variation of this problem is used in various other problems like convolution
• It finds many uses in computational geometry

With this article at OpenGenus, you must have the complete idea of solving 4 Sum problem efficiently.