In this article, we will explore in detail about Scapegoat tree which is a Self Balancing Binary Tree without requiring any extra space which puts Scapegoat Tree at an unique advantage.

Table of contents

• Binary tree
  • Self balancing binary tree
• Scapegoat tree
  • Partial rebuilding
  • In-depth analysis of scapegoat tree
  • Python implementation
• Complexity analysis

Let us get started with Scapegoat tree.

Binary tree

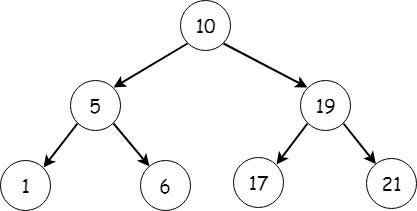
When all non-leaf nodes of a tree data structure has atmost 2 children, then such a data structure is known as a binary tree. The two children of each node are referred as the left child and the right child of the respective node. Given below is an example of a binary tree.

Self balancing binary tree

A self balancing binary tree is a binary tree that keeps track of its height or the number of levels of nodes below the root. Typically the balance factor of a particular node must lie between [-1,0,1], where the balance factor is the difference between the height of its left subtree and the height of its right subtree. If the balance factor of a particular node lies out of the above specifed range, required steps like either rebuilding the tree or performing rotations are taken so that the balance factor is within the range. The main aim of these self balancing binary trees is to keep the height of the tree to a minimum. The AVL tree, red-black tree and scapegoat tree are some examples of self balancing trees.

Scapegoat tree

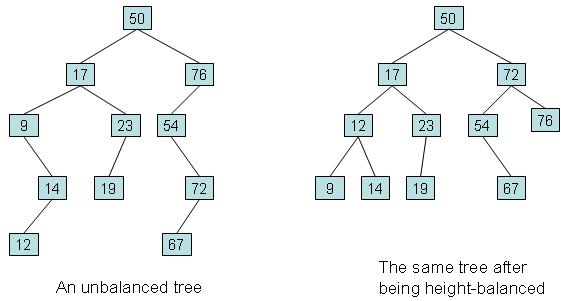
Scapegoat tree is a type of self balancing binary tree which doesn't require any extra storage space per node. This tree is most efficient in insert and look-up operations and can be used in places where these operations are needed.

After an insertion, one node which is unbalanced is found. That node is the scapegoat. Then the tree is rebuilt to create a new ordered and balanced tree. In scapegoat tree, the number of nodes in the left and right subtrees cannot differ by more than 1.

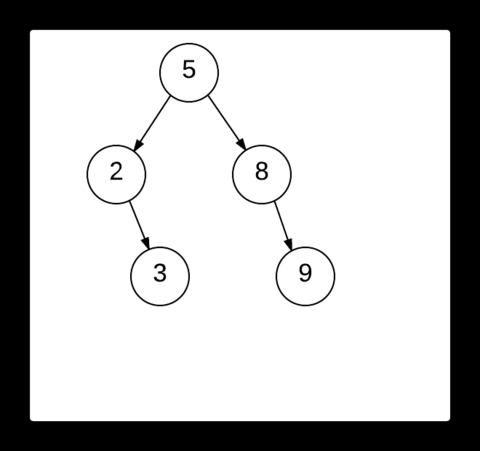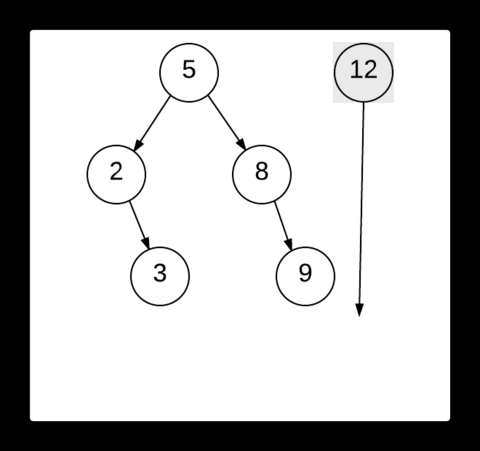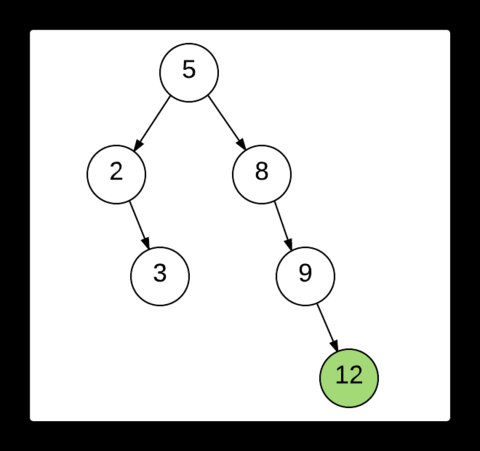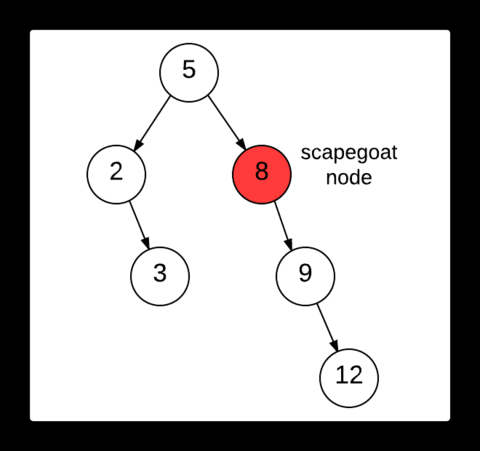
The above image depicts the process of finding the scapegoat. After 12 is inserted into the tree, the balanced tree becomes unbalanced. First the we examine the newly inserted node to see if its balanced. If it is balanced, it's parent node is checked for the same. This process is repeated until we find the scapegoat. Here the node 9 is then checked. We see that it is balanced. So we then move to its parent node, 8. Upon examining the node 8, we find that it is unbalanced and hence it is our required scapegoat.

Partial rebuilding

This is a concept that is exclusive to scapegoat trees. Here, when a scapegoat is encountered and the tree becomes unbalanced, instead of rebuilding the whole tree to give a new balanced binary tree, only the subtree that has the scapegoat as its root is deconstructed and rebuilt to produce a balanced binary tree. This is called partial rebuilding.

In-depth analysis of scapegoat tree

Along with keeping track on the number of nodes (denoted as self.size in the python implementation given below), a scapegoat tree also keeps an eye on the upper-bound of nodes in the tree (denoted as self.maxsize). The parameters size and maxsize must always satisfy

maxsize/2 ≤ size ≤ maxsize

It also maintains a logarithmic height and its condition is

log_3/2(maxsize) ≤ log_3/2(2*size) < log_3/2(size)+2

The thumb rule to be followed is that the height of the tree must not exceed log_3/2(maxsize).

While inserting a node, we use the usual binary search tree algorithm to find the right place to insert the node and increment size and maxsize after inserting it. Sometimes, we may be lucky enough that the height of the tree doesn't exceed log_3/2(maxsize). In that case, we leave the tree undisturbed.
During times we are not that lucky, the height may exceed log_3/2(maxsize) and we must reduce the height of the tree. To do this, we traverse up from the node we inserted to find the scapegoat (say s). One way to see if a node is a scapegoat is that it should satisfy:

( size(s.child) / size(s) ) > 2/3

(s.child is the immediate child of the scapegoat that we encountered while traversing.)
After finding the scapegoat, we perform partial rebuilding that reduces the height of the tree so that the height of the scapegoat tree is again ≤ log_3/2(maxsize).

Python implementation

For implementing scapegoat tree in python, we import the math package with the following command.

import math

The node class

We first create a class called node and define all the node parameters: key to point at the node's data, left and right for it's children and parent to store the value of the parent node of the given node.

class Node:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None
        self.parent = None

Class Scapegoat

We then create a class Scapegoat under which we define all the functions required to implement scapegoat tree.

Initialization

We first initialize all the required parameters for the tree as we did for thr node before.

def __init__(self):
        self.root = None
        self.size = 0
        self.maxSize = 0

Insertion

A function insert is then defined to facilitate the insertion of an element into the tree. This tree follows all the insertion rules of the binary search tree i.e. left node < root < right node. After every insertion, the function to find the scapegoat (if any is present in the tree) is called and the required pointers are assigned.

    def insert(self, key):
        node = Node(key)
        #Base Case - Nothing in the tree
        if self.root == None:
            self.root = node
            return
        #Search to find the node's correct place
        currentNode = self.root
        while currentNode != None:
            potentialParent = currentNode
            if node.key < currentNode.key:
                currentNode = currentNode.left
            else:
                currentNode = currentNode.right
        #Assign parents and siblings to the new node
        node.parent = potentialParent
        if node.key < node.parent.key:
            node.parent.left = node
        else:
            node.parent.right = node
        node.left = None
        node.right = None
        self.size += 1
        #Finding the scapegoat
        scapegoat = self.findScapegoat(node)
        if scapegoat == None:
            return
        tmp = self.rebalance(scapegoat)

        #Assign the correct pointers to and from scapegoat
        scapegoat.left = tmp.left
        scapegoat.right = tmp.right
        scapegoat.key = tmp.key
        scapegoat.left.parent = scapegoat
        scapegoat.right.parent = scapegoat

Finding the scapegoat

We define a function findScapegoat. This function takes a node element as an argument and returns None if it is the root node. Else, the balance factor is checked for this node and then the same is repeated for its parent until the root is reached. In the process, if an unbalanced node is found, it is returned.

    def findScapegoat(self, node):
        if node == self.root:
            return None
        while self.isBalancedAtNode(node) == True:
            if node == self.root:
                return None
            node = node.parent
        return node

Checking if the tree is balanced at a node

A function isBalancedAtNode is defined which takes a node as an argument and returns true if the difference between the height of its left and right subtrees is lesser than or equal to 1. Else, it returns false.

    def isBalancedAtNode(self, node):
        if abs(self.sizeOfSubtree(node.left) - self.sizeOfSubtree(node.right)) <= 1:
            return True
        return False

Calculating the height of a given subtree

A function sizeOfSubtree is defined which takes a node as argument. It calculates the height of the right and left subtrees of that node recursively, adds 1 to the result and returns it.

    def sizeOfSubtree(self, node):
        if node == None:
            return 0
        return 1 + self.sizeOfSubtree(node.left) + self.sizeOfSubtree(node.right)

Rebalancing the tree

We define a function rebalance which is used to rebalance the tree once a scapegoat is found. Under this, we define a function flatten which converts the tree into an array. The left subtree of the root , the root and its right subtree are appended into the array as per the given order.

    def rebalance(self, root):
        def flatten(node, nodes):
            if node == None:
                return
            flatten(node.left, nodes)
            nodes.append(node)
            flatten(node.right, nodes)

Building a tree from the array

A function buildTreeFromSortedList is defined which takes the array, the atarting and end indices as arguments and builds a tree from the list using binary search and assigning the mid value in the list as the tree's root.

        def buildTreeFromSortedList(nodes, start, end):
            if start > end:
                return None
            mid = int(math.ceil(start + (end - start) / 2.0))
            node = Node(nodes[mid].key)
            node.left = buildTreeFromSortedList(nodes, start, mid-1)
            node.right = buildTreeFromSortedList(nodes, mid+1, end)
            return node

Deleting a node

When we delete a node from a scapegoat tree, four cases are possible. Let x be the node to be deleted. Then,

1. x might be a leaf node.
2. x might only have a right child
3. x might only have a left child
4. x might have both the children.

In the first case, the node is deleted as it is. In the second and third cases, the deleted node is replaced by its only successor.

In the fourth case, we find the minimum node of x's right subtree and substitute it in place of x.The function to find the minimum value node is given below:

def minimum(self, x):
        while x.left != None:
            x = x.left
        return x

The code for the delete function is as follows.

    def delete(self, delete_me):
        node = self.root
        parent = None
        is_left_child = True
        # find the node, keep track of the parent, and side of the tree
        while node.key != delete_me:
            parent = node
            if delete_me > node.key:
                node = node.right
                is_left_child = False
            else:
                node = node.left
                is_left_child = True

        successor = None
        # case 1
        if node.left == None and node.right == None:
            pass
        # case 2
        elif node.left == None:
            successor = node.right
        # case 3
        elif node.right == None:
            successor = node.left
        # case 4
        else:
            # find successor
            successor = self.minimum(node.right)
            # the successor is the node's right child -- easy fix
            if successor == node.right:
                successor.left = node.left
          

        # Replacing the node
        if parent == None:
            self.root = successor
        elif is_left_child:
            parent.left = successor
        else:
            parent.right = successor

        self.size -= 1
        if self.size < self.a * self.max_size:
            #print "Rebuilding the whole tree"
            self.root = self.rebalance(self.root, self.size)
            self.max_size = self.size

Complexity analysis

The insertion and searching in scapegoat tree has a complexity of O(log₂(n)) as the new node's appropriate place is found using binary search. Scapegoat tree has a space complexity of O(n) where n is the number of nodes in the tree.

With this article at OpenGenus, you must have the clear idea about Scapegoat Tree. Enjoy.