
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Problem Statement
You are given a list of words, a prefix, and a suffix. You have to find the longest word in the given word list that has a given prefix and suffix. i.e. if the given prefix and suffix are P and S respectively then you have to find the longest word of pattern P*S.
If multiple words satisfy the given condition then return the lexicographically small one. If no word satisfies the condition return an empty string.
For example:
wordlist = ["apple", "appe", "word", "alloye"]
prefix = "a"
suffix = "e"
Output: alloye
As alloye is the longest word that starts and ends with the given prefix and suffix respectively.
Approach 1: Without Trie
The obvious solution to the problem is to loop through each word in the word list. Check if the word starts and ends with the given prefix and suffix. If it does check if its length is greater than the previous or not. At the end return the longest word.
Algorithm
Step1: Create a variable longest and initialize it as an empty string
Step2: For each word in the wordlist loop from the beginning to the end:
Step3: If the word starts and ends with the given prefix and suffix:
Step4: If the length of the word is greater than the length of longest:
Step5: Set longest to word
Step6: If the length of the word is equal to the length of longest:
Step7: If the word is lexicographically smaller than longest:
Step8: Set longest to word
Step9: Return word
Exmaple
Let's say that the given wordlist is ["apple", "appe", "word", "alloye"] and we have to find the longest word that has prefix a and suffix e.
Let's create a variable longest and initialize it as an empty string i.e. longest = "".
Now, check if the word apple starts with a and ends with e. This holds true for apple. So, set the longest to be apple i.e. longest = apple.
Next, check if the word appe starts with a and ends with e. This holds true here. But its lenght is smaller than the previous longest word. So, we won't set it the longest. i.e. longest = apple.
Next, we check if the word word starts and ends with a and e respectively. It does not hold true. So, we move to the next word and still longest = apple.
Next, we check if the word alloye starts with a and ends with e. It holds true as well as its lenght is greater than the current longest word. So, we set it to the longest i.e. longest = alloye.
Since, there is no word left in the wordlist we return the current longest word i.e. we return alloye.
Java Implementation
class LongestPrefixAndSuffix {
public static String longestWord(String[] words, String prefix, String suffix) {
String longest = "";
for(String s: words) {
if(s.startsWith(prefix) && s.endsWith(suffix)) {
if(s.length() > longest.length()) {
longest = s;
}
if(s.length() == longest.length()) {
longest = (s.compareTo(longest) < 0)? s: longest;
}
}
}
return longest;
}
public static void main(String[] args) {
String[] words = {"apple", "ape", "word", "alloe"};
String word = longestWord(words, "a", "e");
System.out.println(word);
}
}
C++ Implementation
#include <iostream>
#include <vector>
using namespace std;
bool starts_with(string str, string prefix)
{
if(str.length() < prefix.length())
return false;
for(int i = 0;i < prefix.length();i++)
{
if(str[i] != prefix[i])
return false;
}
return true;
}
bool ends_with(string word, string suffix)
{
int lw = word.length();
int ls = suffix.length();
if(lw < ls)
return false;
int j = ls - 1;
for(int i = lw - 1;j >= 0;i--,j--)
{
if(word[i] != suffix[j])
return false;
}
return true;
}
string longestWord(vector<string>& s, string prefix, string suffix)
{
string longest = "";
for(auto word: s)
{
if(starts_with(word, prefix) and ends_with(word, suffix))
{
if(word.length() > longest.length()) {
longest = word;
}
if(word.length() == longest.length() and word < longest) {
longest = word;
}
}
}
return longest;
}
int main()
{
vector<string> s = {"apple", "ape", "word", "aqoye"};
string str = longestWord(s, "s", "e");
cout << str << endl;
}
Note: In C++20 we don't need to implement our starts_with() and ends_with() function as it has been included in the string class.
Time Complexity
The time complexity of the algorithm is the time complexity of the function longestWord(). Suppose that the time taken by function longestWord() is T(lw), time taken by the function starts_with() is T(sw) and the time taken by the function ends_with() is T(ew).
Again comparing the strings takes O(n) time, n being the length of the string. Then,
T(lw) = N * (T(sw) + T(ew))
We can see that the T(sw) = O(p), p being the length of the prefix,
T(ew) = O(s), s being the length of the suffix
So, the total time complexity will be O(N * M)
where N is the length of the wordlist and M is the average length of the word in the wordlist.
Space Complexity
As we are not using any extra space the space complexity will be O(1).
Approach 2: Using Trie
For dictionary search, a trie data structure is considered the best data structure. So, we can employ the trie data structure to solve the problem.
The idea of using a trie data structure to solve the problem is very simple. We can create two tries prefixTrie and suffixTrie respectively. We can now insert all the words into the prefixTrie in the forward direction which will enable us to search for the existence of any word with the given prefix and into the suffixTrie in the backward direction or reverse direction that will enable us to search for the existence of any word with given suffix.
Steps
Step1: Create two tries namely prefixTrie and suffixTrie
Step2: Insert all the words into the prefixTrie from the front to the end of the word
Step3: Insert all the words into the suffixTrie from the back to the front of the word
Step4: Query prefixTrie to return indexes of all the strings that start with the given prefix and store them in list1
Step5: Query suffixTrie to return indexes of all the strings that end with the given suffix and store them in list2
Step6: Loop through lists, list1, and list2, to get indexes of all the words that start with and end with given prefix and suffix respectively:
Step7: Compare lengths of the words that start with the given prefix and end with the given suffix and find the longest one
Step8: Return the longest word
Note: The above-mentioned steps require the students to have prior knowledge of trie data structure and insert and search operations in it.
Exmaple
Let's suppose that wordlist = ["apple", "appe", "word", "alloye"].
Here's the prefix trie for the given wordlist.
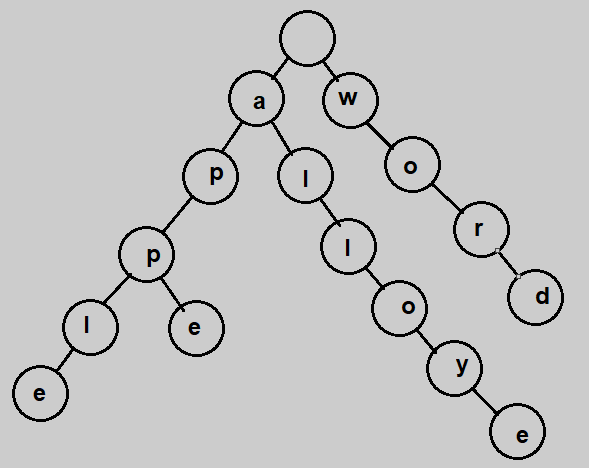
Here's the suffix trie for the given wordlist.
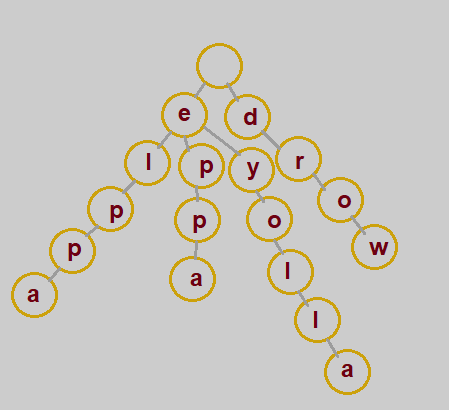
When we query prefixTrie for the index of all the words that starts with a it returns [0, 1, 3]. And when queried for the list of words that starts with suffix, suffixTrie returns [0, 1, 3].
Now, we find common indexes in both the returned lists and we get [0, 1, 3].
Create a variable longest and initialize it as an empty string.
Next, we compare longest with the word, apple, at index 0 and set the longest to apple.
Again, compare the longest with the word, appe, at index 1 and still the longest is apple.
Now, we compare the longest with the word, alloye, at index 3 and found it to be longer than apple. So, set it to the longest i.e. longest = alloye.
Since, there's no index left for the comparison we return the current longest i.e. alloye.
Java Implementation
import java.util.*;
class Solution {
public static String longestWord(String[] words, String prefix, String suffix) {
Trie prefixTrie = new Trie();
Trie suffixTrie = new Trie();
//inserts all the words into the prefixTrie from the front of the word
prefixTrie.insertAll(words);
//inserts all the words into the suffixTrie from the back of the word
suffixTrie.insertAllReverse(words);
//the indexes of all the words that start with the given prefix in sorted order
ArrayList<Integer> prefixAt = prefixTrie.searchPrefix(prefix);
//the indexes of all the words that ends with given suffix in sorted order
ArrayList<Integer> suffixAt = suffixTrie.searchSuffix(suffix);
//holds the indexes of all the words that start with and end with the given prefix and suffix respectively
ArrayList<Integer> wordsAt = new ArrayList<>();
int n = prefixAt.size();
int m = suffixAt.size();
int i = 0, j = 0;
while(i < n && j < m) {
if(prefixAt.get(i) == suffixAt.get(j)) {
wordsAt.add(prefixAt.get(i));
i++;
j++;
}
else if(prefixAt.get(i) > suffixAt.get(j))
j++;
else
i++;
}
String longest = "";
for(i = 0;i < wordsAt.size();i++) {
if(words[wordsAt.get(i)].length() > longest.length())
longest = words[wordsAt.get(i)];
if(words[wordsAt.get(i)].length() == longest.length() && words[wordsAt.get(i)].compareTo(longest) < 0)
longest = words[wordsAt.get(i)];
}
return longest;
}
public static void main(String[] args) {
String[] words = {"apple", "ape", "word", "aqoye"};
String longest = longestWord(words, "a", "e");
System.out.println(longest);
}
}
class Trie {
class Node {
Node[] links;
ArrayList<Integer> indeces;
Node() {
links = new Node[26];
indeces = new ArrayList<Integer>();
}
//checks if the character is present
boolean containsKey(char ch) {
return links[ch - 'a'] != null;
}
//returns the node referenced by the character
Node get(char ch) {
return links[ch - 'a'];
}
//adds a node to links array
void put(char ch, Node node) {
links[ch - 'a'] = node;
}
//adds the index of the word in indeces
void addIndex(int index) {
indeces.add(index);
}
//returns all index of all the words that has given prefix or suffix
ArrayList<Integer> getList() {
return indeces;
}
}
Node root;
Trie() {
root = new Node();
}
void insert(String word, int index) {
Node node = root;
for(char ch: word.toCharArray()) {
if(!node.containsKey(ch))
node.put(ch, new Node());
node = node.get(ch);
node.addIndex(index);
}
}
//adds the reverse of the word into the trie
void insertReverse(String word, int index) {
Node node = root;
for(int i = word.length() - 1;i >= 0;i--) {
if(!node.containsKey(word.charAt(i)))
node.put(word.charAt(i), new Node());
node = node.get(word.charAt(i));
node.addIndex(index);
}
}
void insertAll(String[] words) {
for(int i = 0;i < words.length;i++) {
insert(words[i], i);
}
}
void insertAllReverse(String[] words) {
for(int i = 0;i < words.length; i++) {
insertReverse(words[i], i);
}
}
ArrayList<Integer> searchPrefix(String str) {
Node node = root;
for(char ch: str.toCharArray()) {
if(!node.containsKey(ch))
return new ArrayList<Integer>();
node = node.get(ch);
}
return node.getList();
}
ArrayList<Integer> searchSuffix(String str) {
Node node = root;
int len = str.length();
for(int i = len - 1;i >= 0;i--) {
if(!node.containsKey(str.charAt(i)))
return new ArrayList<Integer>();
node = node.get(str.charAt(i));
}
return node.getList();
}
}
C++ Implementation
#include <iostream>
#include <vector>
using namespace std;
struct Node {
Node* links[26];
vector<int> indexes;
bool containsKey(char ch) {
return links[ch - 'a'] != nullptr;
}
void put(char ch) {
links[ch - 'a'] = new Node();
}
Node* get(char ch) {
return links[ch - 'a'];
}
void addIndex(int index) {
indexes.push_back(index);
}
vector<int> getIndexes() {
return indexes;
}
};
class Trie {
private:
Node* root;
public:
Trie() {
root = new Node();
}
void insert(string word, int index) {
Node* node = root;
for(char ch: word) {
if(!node->containsKey(ch))
node->put(ch);
node = node->get(ch);
node->addIndex(index);
}
}
void insertReverse(string word, int index) {
Node* node = root;
for(int i = word.size() - 1;i >= 0;i--) {
if(!node->containsKey(word[i]))
node->put(word[i]);
node = node->get(word[i]);
node->addIndex(index);
}
}
void insertAll(vector<string> words) {
int i = 0;
for(string word: words) {
insert(word, i++);
}
}
void insertAllReverse(vector<string> words) {
for(int i = 0;i < words.size();i++) {
insertReverse(words[i], i);
}
}
vector<int> searchPrefix(string str) {
Node* node = root;
for(char ch: str) {
if(!node->containsKey(ch))
return vector<int>(0);
node = node->get(ch);
}
return node->getIndexes();
}
vector<int> searchSuffix(string word) {
Node* node = root;
for(int i = word.size() - 1;i >= 0;i--) {
if(!node->containsKey(word[i]))
return vector<int>(0);
node = node->get(word[i]);
}
return node->getIndexes();
}
};
string longestWord(vector<string> words, string prefix, string suffix) {
Trie* prefixTrie = new Trie();
Trie* suffixTrie = new Trie();
//inserts all the words into trie from its front to back
prefixTrie->insertAll(words);
//inserts all the words into trie from its back to front i.e. in reverse order
suffixTrie->insertAllReverse(words);
//indexes of all the words that starts with given prefix
vector<int> list1 = prefixTrie->searchPrefix(prefix);
//indexes of all the words that ends with given suffix
vector<int> list2 = suffixTrie->searchSuffix(suffix);
//indexes of all the words that start and end with the given prefix and suffix respectively
vector<int> list;
int n = list1.size();
int m = list2.size();
int i = 0, j = 0;
while(i < n and j < m) {
if(list1[i] == list2[j]) {
list.push_back(list1[i]);
i++;
j++;
}
else if(list1[i] > list2[j]) {
j++;
}
else {
i++;
}
}
string longest = "";
i = 0;
for(i = 0;i < list.size();i++) {
if(words[list[i]].size() > longest.size())
longest = words[list[i]];
if(words[list[i]].size() == longest.size() && words[list[i]] < longest)
longest = words[list[i]];
}
return longest;
}
int main() {
vector<string> s = {"apple", "ape", "word", "alloye"};
string str = longestWord(s, "ap", "e");
cout << str << endl; //output: apple
}
Time Complexity
Inserting all the words into trie takes ΣO(ni) where ni is the length of ith string in the wordlist. Searching the prefix and suffix takes O(p) and O(s) time respectively where p and s are the lengths of the prefix and suffix respectively. In the worst-case finding the words that start and end with a given prefix and suffix respectively take O(n) time, where n is the length of the wordlist.
Adding all these together gives us the time complexity of finding the longest word that satisfies the condition. So, the time complexity of the function longestWord() will be ΣO(ni + p + s + n). Removing the lower order terms gives us the time complexity of ΣO(ni).
If we consider m is the average length of the word in the wordlist then the time complexity is O(n * m).
Space Complexity
As we are creating two tries and inserting all the characters into a trie, space complexity can be approximated to ΣO(ni).
Happy Coding!🤗🤗🤗
See you!👋👋👋
