In this article, we have explained the algorithm to find the shortest path in a Directed Acyclic Graph using Topological Sort.

Table of content:

1. Problem Statement
2. Approach
3. Pseudo Code for Topological Sorting (DFS)
4. Pseudo Code for finding Shortest path using Topological Sorting
5. Time Complexity
6. Comparison of Topological Sorting with other shortest distance finding algorithms
7. Application of Topological Sorting
8. Question

We will dive into it now.

Problem Statement

We are given with a weighted directed acyclic graph and a source vertex, we need to compute the shortest path from source vertex to every other vertex given in the graph.(It is assumed that weight associated with every edge of graph represents the path length between two vertices)

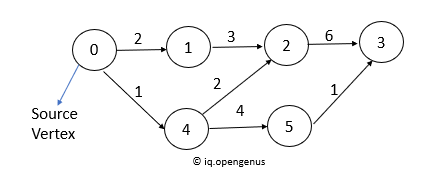
Approach

• Since we are given that given graph is a Directed Acyclic Graph we can think of applying Topological Sort on the graph so as to compute shortest path from source vertex.

• What is Topological Sort?

1. Topological sorts works only for Directed Acyclic Graph(DAG).
2. Topological sorting of vertices of Directed Acyclic Graph is an ordering of vertices v1,v2,---Vn of a graph in such a way that "if there is an edge from vi to vj vertex then vi should always come before vj in the topological sorting of the graph"
3. So Basically in topological sorting of a graph the vertices which have fewer dependencies are printed before the vertices which have relatively greater dependencies.
4. We can use both DFS/BFS for implementing Topological Sorting.

How can we use topological Sorting to find shortest path?

1. Topological Sorting basically sorts the vertices of graph in increasing order of their dependencies(by dependencies of vertex we mean indegree of a edge) or their indegree and Since shortest path between source vertex and a particulat vertex should involve minimum intermediate edges hence finding topologcial sort first for computing shortest path makes sense becaues topological sort arranges the vertices in increasing order of their indegree.
2. Idea is to traverse through the vertices of graph according to topological sorting of the graph and for every current vertex in the topological sort we traverse through the adjacency list of current vertex we implement the following operation:

for(auto i : adj[u])
{
  if dist[i]>dist[u]+weight(u,i)
     dist[i] = dist[u]+weight(u,i);
}

• Here "u" is current Vertex in the Topological Sorting

• adj[u] represents the adjacency list of the vertex"u".

• "i" is the current vertex in the adjacency list of "u".

• dist[] is a vector whose index number represents a vertex in the graph and corresponding value stored in a index represents the length of shortest path between the vertex represented by the index number and source vertex. Initially value of dist[i] for every index except the index number for source vertex is INT_MAX.

• So basically we check whether we can reach vertex "i" from source vertex via vertex "u" in a shorter length path than the current path and if we get shorter path then we update the values of dist[i].

Pseudo Code for Topological Sorting (DFS)

Topological Sorting can be simply implemented by Depth First Traversal of the graph. We will use a stack to store the vertices traversed via Depth First Traversal of the graph such that the vertex with the greatest indegree is at the bottom of the stack and the vertex which has the smallest indegree is at the top of the stack.

void topological(vector<int> adj[], int v)
{
  vector<bool> visited(v,false);
  stack<int> stk;
  for(int i=0;i<v;i++)
  {
    if(visited[i]==false)
      {
        DFSrec(adj,i,visited,stk);
      }
   }
}

void DFSrec(vector<int> adj, int u, vector<bool> &visited, stack<int>& stk)
{
   visited[u] = true;
   for( auto i : adj[u])
   {
     if(visited[i] == false)
       {
         DFSrec(adj,i,visited,stk)
       }
    }
    stk.push(u);
 }

Finally after implementing this topological sorting function based on Depth First Traversa of graph we will get a stack whose top element represents the vertex with the smallest indegree and the bottom element of the stack represents the vertex with the largest indegree.

Pseudo Code for finding Shortest path using Topological Sorting

• We will traverse through the stack that contains topological sorting of the graph which we have formed using depth first traversal.
• We will form a vector dist[] as explained earlier and we will intialise every every index except the index which reprsents source vertex as INT_MAX
• In each iteration we will traverse through the adjacency list of the vertex of graph which is represented by the current top element of the stack and the end of current iteration we pop-out the current top of the stack.

void shortestpath(vector<int> adj, stack<int>& stk, int source)
{
  int v = adj.size();
  vector<int> dist(v,INT_MAX);
  dist[source] = 0;
  
  while(stk.empty() != true)
  {
    int u = stk.top();
    stk.pop();
    for(auto i: adj[u])
    {
      if(dist[i] > dist[u]+weight(u,i))
        dist[i] = dist[u] + weight(u,i);
    }
}

Finally dist[] vector will store the distance of vertex represented by index number from the source vertex and if dist[i] is Infinity for any vertex then this means that there is no path possible between the source vertex and the vertex represented by index number "i".

Time Complexity

• Time complexity for doing Topological Sorting using DFS takes O(v+e) where "v" is number of vertices and "e" is the number of edges in the graph.

  • Reason: Topological sorting using DFS is a normal
    DFS program with very minor modification of pushing vertices into stack which takes O(1) time hence essentially we can say that time complexity is same as normal DFS function.

• Time Complexity for shortest path function is O(v+e)
  where v is number of veritces in the graph and e is the number of edges in the graph.

• Reason: Using the while loop for traversing through stack and for loop for traversing through adjacency list of vertices we are simply traversing through the graph and hence it will take O(v+e).

• Overall Time complexity is O(v+e+v+e) which is essentially equal to O(v+e).

Comparison of Topological Sorting with other shortest distance finding algorithms

• Bellman Ford Algorithm can be used for a general weighted graph and time complexity for Belman Ford Algorithm is O(v*e).
• Dijkstra's Algorithm have a time complexity of O(e*logv) which is better than Bellman Ford Algorithm but the problem with Dijkstra's Algorithm is that it cannot be used for graphs that have negative weighted edges.
• For a unweighted graph we can use BFS algorithm with time complexity of O(v+e).
• For a Directed Acyclic Graph we can use Topological Sorting which have a time complexity of O(v+e).

Application of Topological Sorting

Topological Sorting can be used in Job Scheduling.

Here each vertex of graph can be considered as job and if there is a edge from vertex v1 to v2 then this means that job2 has a dependency on job1 and hence job1 should be completed before job2 hence we need to topological sorting inorder to get the most suiteable sequence in which each job be completed.

Question

Why is Topological Sorting only applicable for Directed Acyclic Graph?

The answer has been answered in this article in a previous section. Go through it again if you are unable to answer it.

With this article at OpenGenus, you must have a strong idea of finding Shortest Path using Topological Sort. Enjoy.