Space partitioning trees

Space partitioning trees are Tree data structures drawn by partitioning the space. It is a method, of dividing any space into non overlapping regions. Any point may be identified in that region, which helps in organising user data according to their spatial position.

They are

• Hierarchical - Regions divide into subregions and so on.
• Recursive - The system is applied such that it recursively generates regions. Click here to know more about Recursion
• Tree - This can be organised in the form of a tree, such that objects are added relative to their position.

They primarily deal with loactions in any n-dimensional space, and are represented through a variety of trees. Following are few trees, which shall give you an idea about what is this all about and how does this work.

Different types of Space partitioning trees are:

• Binary Space Partitioning Tree
• Quadtrees
• Octrees
• K-D Trees
• Other tree data structures like R trees

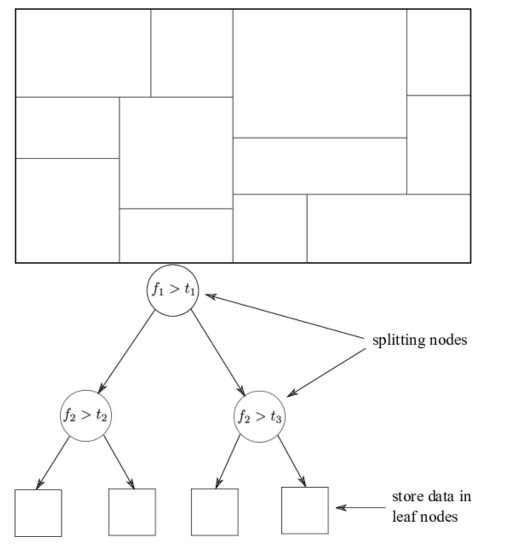
Binary Space Partitioning Tree

Binary space partitioning tree is a tree where each node recursively divides space into two .
It is a hierarchial subdivision of an n-dimensional space into convex subspaces. BSP trees may perform addition, deletion, movement a little costlier but search is very efficient.

Root node -> All the space available
All other nodes -> A limited, subdivision of parent node's space

A visual Representation

We will be looking at a 2-D plane for this explanation.

Firstly, a partition hyperplane needs to be selected

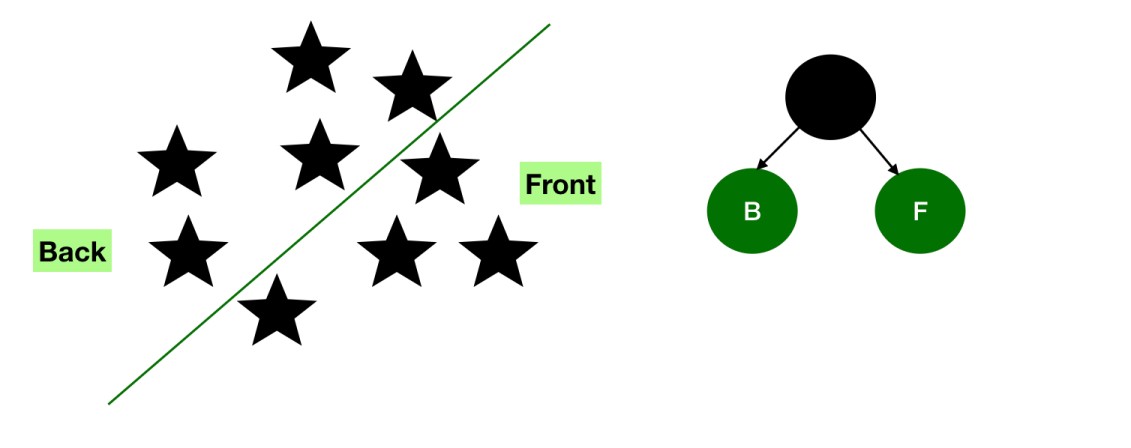
This divides the space into two subplanes, namely the front and the back.
These two planes maybe further subdivided to get more subplanes.

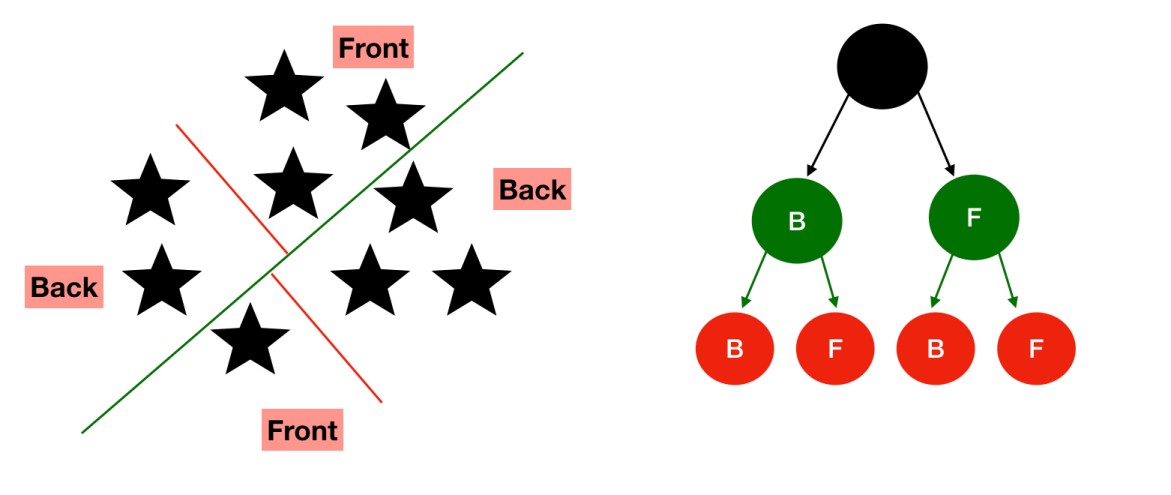
This process is recursively repeated at the back and front of each node list, untill we reach distinct nodes.

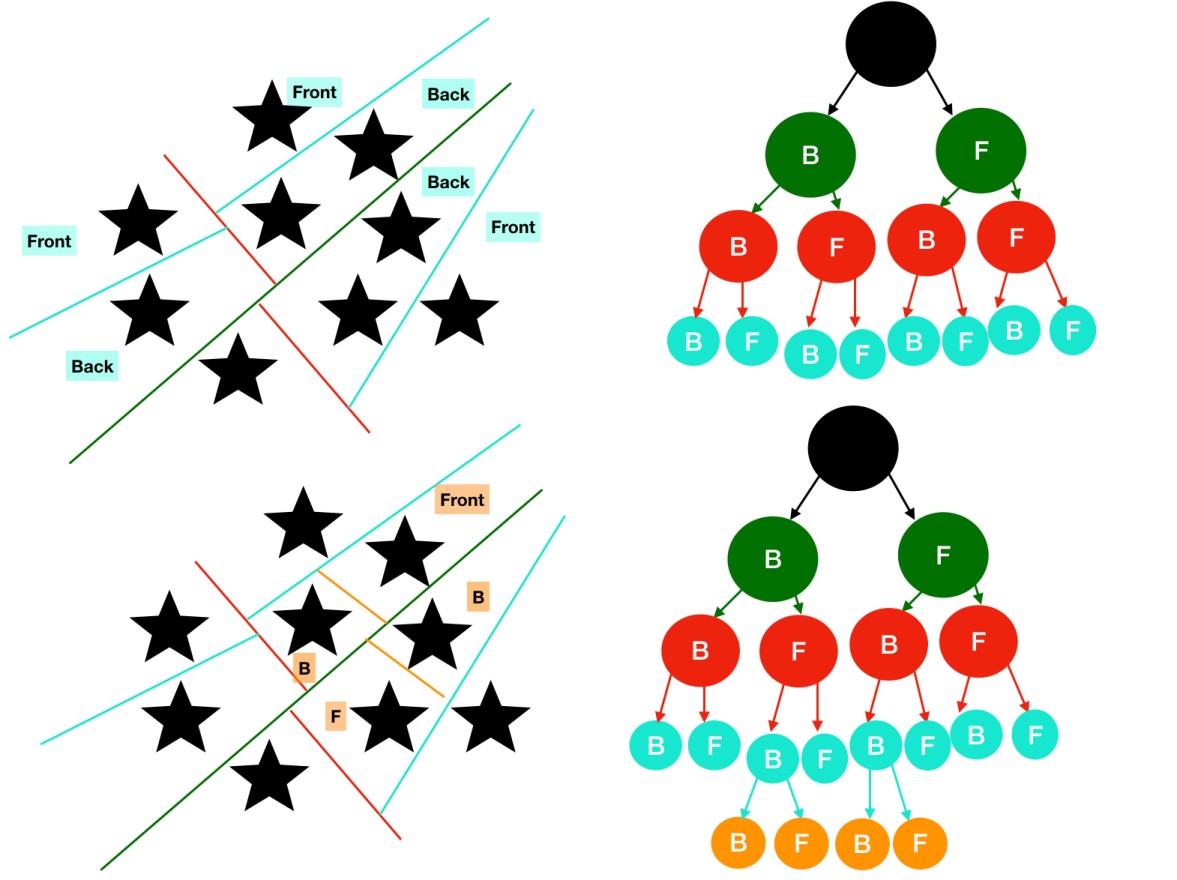
Algorithms

Now, the recursive alogrithm for the same, may seem very easy to understand

bsptree (poly* curr_poly)
{
    while(still_poly)
    {
        partition_poly( curr_poly );
    }
    bsptree(curr_poly->left);
    bsptree(curr_poly->right);
}

Note - Since, recursion may not give the best performance, mostly tree calculations are done priorly.

Rendering or traversal maybe performed as follows

traverse_tree(bsp_tree* tree,point eye)
{
    location = tree->find_location(eye);

    if(tree->empty())
      return;

      if(location > 0) // if eye infront of location
      {
        traverse_tree(tree->back,eye);
        display(tree->polygon_list);
        traverse_tree(tree->front,eye);
      }
      else if(location < 0) // eye behind location
      {
          traverse_tree(tree->front,eye);
        display(tree->polygon_list);
        travers_tree(tree->back,eye);
      }
      else  // eye coincidental with partition hyperplane
      {
           traverse_tree(tree->front,eye);
           traverse_tree(tree->back,eye);
      }
}

It finds major applications in geometric modelling.
With this, you may have an idea about, Binary Space partitioning trees.

Quadtrees

As the name contains "Quad" and we're discussing "Partitioning Trees", it is evident that in this tree, each internal node contains exactly four children.

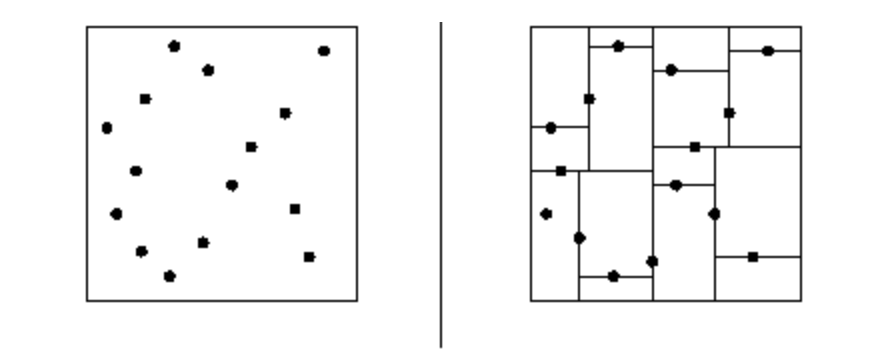
Below, Quad Tree Compression has been illustrated. The image is being compressed such that each partition is being subdivided into four partitions. The left image, also displays the partitions whereas the right image shows the compressed image.

You may observe that every partition is being subpartitioned untill requisite visibility and sharpness has been attained.

This is just one of the many applications of quadtrees.

This may also be used to efficiently store data points in a 2-Dimensional space.

Following is a Point-Region Quadtree.

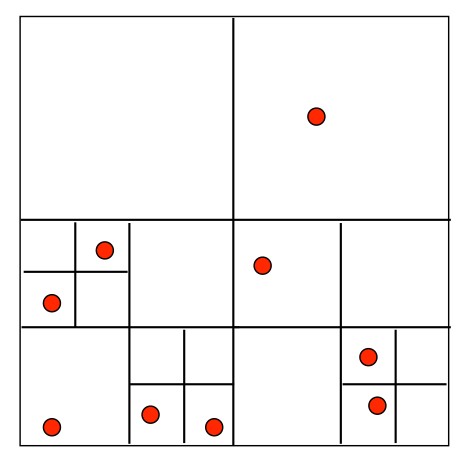
A region is subdivided untill it contains one or no point.

The tree is formed as follows

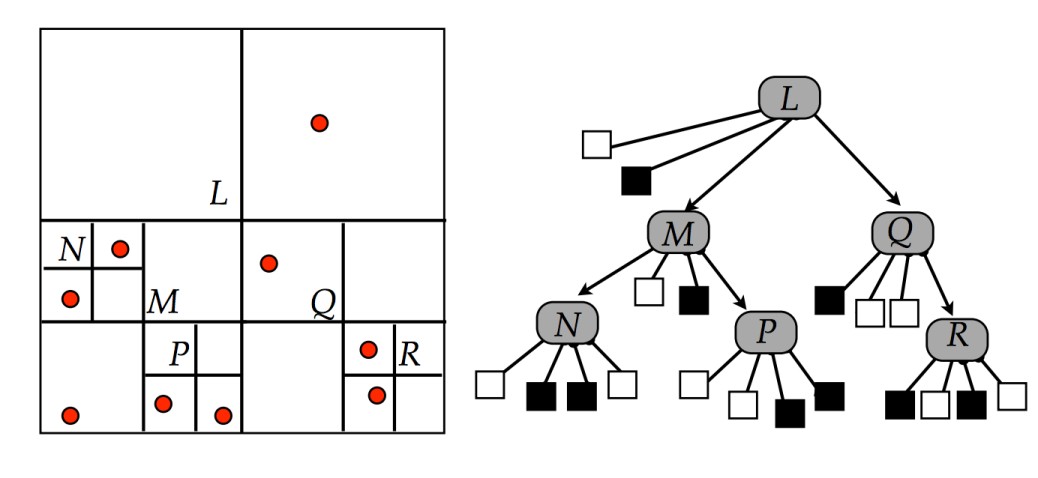
The algorithm for the insertion maybe

1. Start with root node as current node.
2. If the given point is not in boundary represented by current node, stop insertion
    with error.
3. Determine the appropriate child node to store the point.
4. If the child node is empty node, replace it with a point node representing the
    point. Stop insertion.
5. If the child node is a point node, replace it with a region node. Call insert for
    the point that just got replaced. Set current node as the newly formed region
    node.
6. If selected child node is a region node, set the child node as current node.
    Goto step 2.

It is an important method in Computational Geometry, and finds several applications such as games, physically based simulations and generate "smart" meshes.

Read more about Quadtrees

Octrees

As the name suggests, and is also more obvious after just going through Quadtrees,
In Octree each internal node contains exactly eight children.

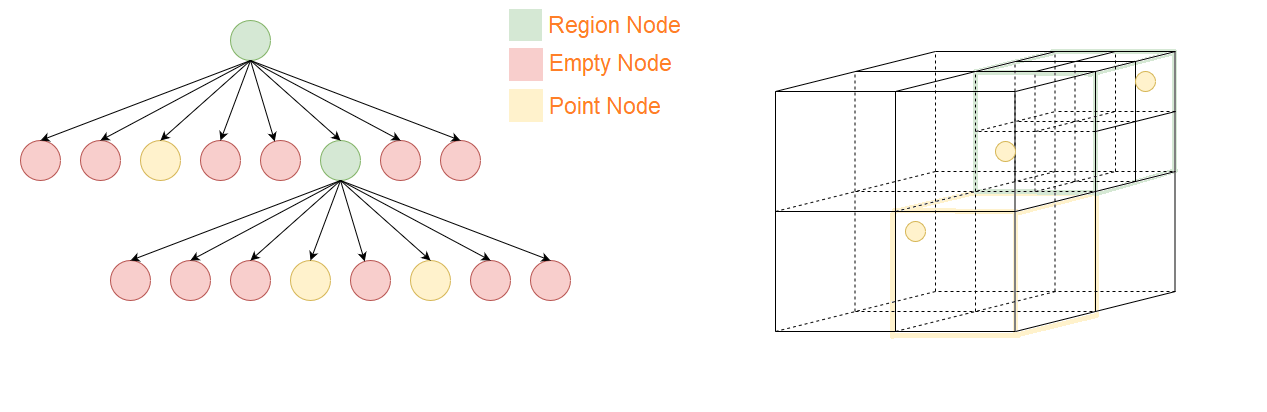
It finds primary application in 3-Dimensional space, as it divided tha space into 8 octants (rather than 4 quadrants).

It is also useful in dealing with coloured photos, as they contain of RGB (Red-Green-Blue), i.e 3 colours, and 2^3 equals 8.

The algorithm for the insertion maybe

1. Start with root node as current node.
2. If the given point is not in cuboid represented by current node, stop insertion
    with error.
3. Determine the appropriate child node to store the point.
4. If the child node is empty node, replace it with a point node representing the
    point. Stop insertion.
5. If the child node is a point node, replace it with a region node. Call insert for
    the point that just got replaced. Set current node as the newly formed region
    node.
6. If selected child node is a region node, set the child node as current node.
    Goto step 2.

They find application in representing a 3-dimensional space and used in 3D Computer Graphics. It is also used for nearest neighbour search which can be easily done in logarithmic time.
Read more about Octrees

K-D Trees

K-D refers to K Dimensions, K-D trees are K-Dimensional Trees, i.e. essentially a binary search tree, in a k-dimensional space. Each node, represents a point in the k-dimensional space.

Following is a space representation of the same, and the tree so formed.

The two spaces each non-leaf node divides (just as we saw in binary space partitioning tree, but in a k-dimensional space), divides the space in two parts, known as half spaces.

Each level has a cutting dimension.

Insertion maybe observed according to the following algorithm

insert(Point X, KDNode t, int cd)
{
    if ( t == NULL )
        t = new KDNode(x)
    else if( x == t.data )
        //error! duplicate
    else if ( x[cd] < t.data[cd])
        t.left = insert(x, t.left, (cd + 1) % DIM)
    else
        t.right = insert(x, t.right, (cd + 1) % DIM)
    return t;
}

On the left you may see the input of points and on the right is the output arrangement.

K-D trees is a useful data structure for several applications, such as searches involving multidimensional search key.

With this, you must have an idea of how do k-d trees function.

These are some of the space partitioning trees, there are more of them too! Namely

• R - trees
• Bins
• Bounding Volume Hierarchies
• et cetera

Anytime you deal with a program requiring spatial position, you must come across space partitioning trees, these are some of the most classic and useful trees with very efficient search algorithms for an n-dimentional space.

With this article at OpenGenus, you probably are now sound with the idea of space partitioning and space partitioning trees and know where to delve deeper and making use of this knowledge to cater to real problems.

Learn more:

• Binary Space Partitioning Tree by Priyanshi Sharma at OpenGenus
• Octree data structure by Yash Aggarwal at OpenGenus
• K dimensional tree by Yash Aggarwal at OpenGenus
• Quad tree by Yash Aggarwal at OpenGenus
• Data Structure topics at OpenGenus