ResNet50 is a variant of ResNet model which has 48 Convolution layers along with 1 MaxPool and 1 Average Pool layer. It has 3.8 x 10^9 Floating points operations. It is a widely used ResNet model and we have explored ResNet50 architecture in depth.

We start with some background information, comparison with other models and then, dive directly into ResNet50 architecture.

Introduction

In 2012 at the LSVRC2012 classification contest AlexNet won the the first price, After that ResNet was the most interesting thing that happened to the computer vision and the deep learning world.

Because of the framework that ResNets presented it was made possible to train ultra deep neural networks and by that i mean that i network can contain hundreds or thousands of layers and still achieve great performance.

The ResNets were initially applied to the image recognition task but as it is mentioned in the paper that the framework can also be used for non computer vision tasks also to achieve better accuracy.

Many of you may argue that simply stacking more layers also gives us better accuracy why was there a need of Residual learning for training ultra deep neural networks.

Problems

As we know that Deep Convolutional neural networks are really great at identifying low, mid and high level features from the images and stacking more layers generally gives us better accuracy so a question arrises that is getting better model performance as easy as stacking more layers?

With this questions arises the problem of vanishing/exploding gradients those problems were largely handled by many ways and enabled networks with tens of layers to converge but when deep neural networks start to converge we see another problem of the accuracy getting saturated and then degrading rapidly and this was not caused by overfitting as one may guess and adding more layers to a suitable deep model just increased the training error.

This problem was further rectifed by by taking a shallower model and a deep model that was constructed with the layers from the shallow model and and adding identity layers to it and accordingly the deeper model shouldn't have produced any higher training error than its counterpart as the added layers were just the identity layers.

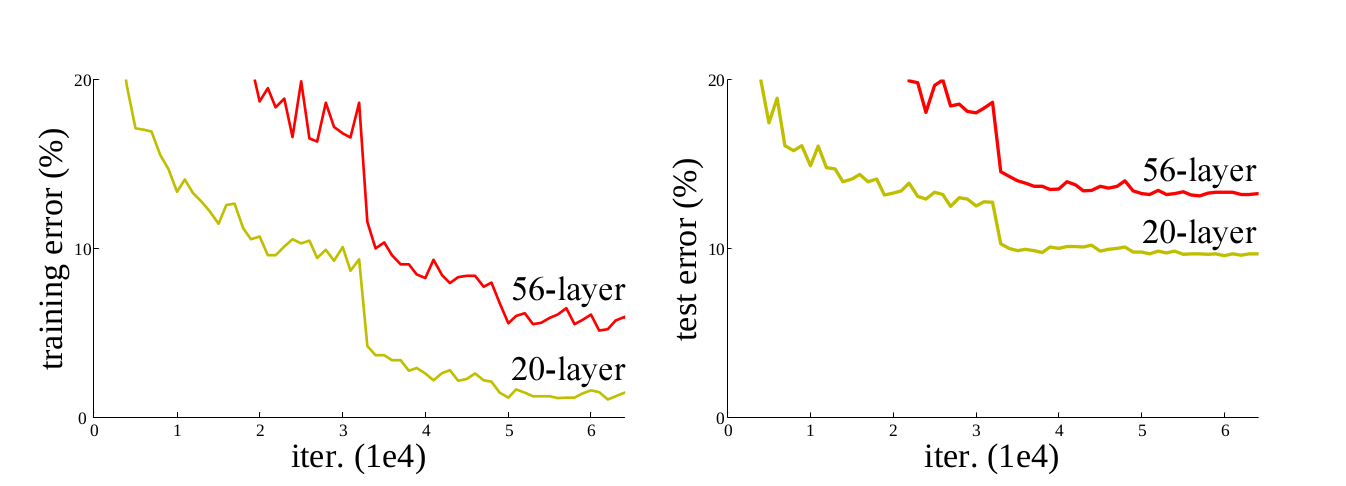
Figure 1

In Figure 1 we can see on the left and the right that the deeper model is always producing more error, where in fact it shouldn't have done that.

The authors addressed this problem by introducing deep residual learning framework so for this they introduce shortcut connections that simply perform identity mappings

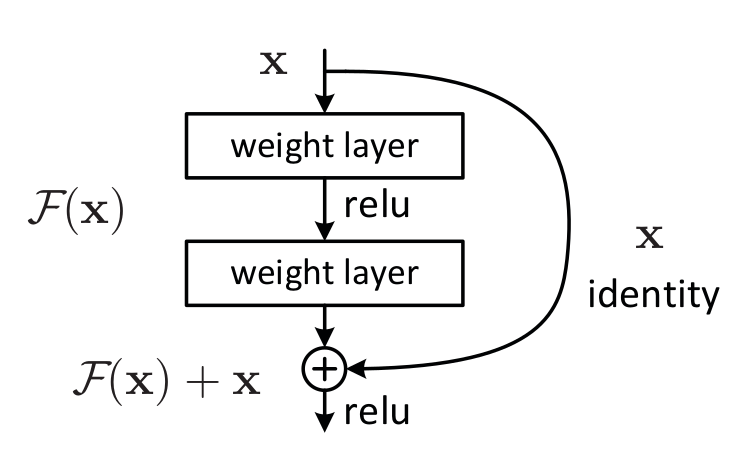
Figure 2

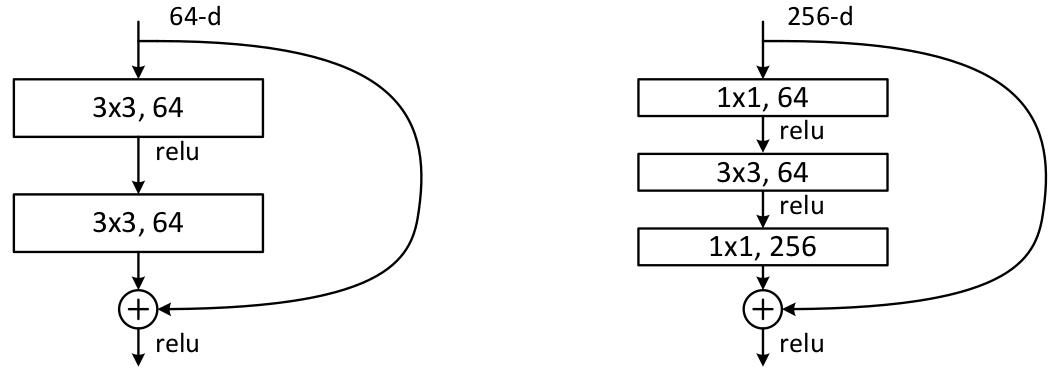
They explicitly let the layers fit a residual mapping and denoated that as H(x) and they let the non linear layers fit another mapping F(x):=H(x)−x so the original mapping becomes H(x):=F(x)+x as can be seen in Figure 2.

And the benifit of these shortcut identity mapping were that there was no additional parameters added to the model and also the computational time was kept in check.

Comparison

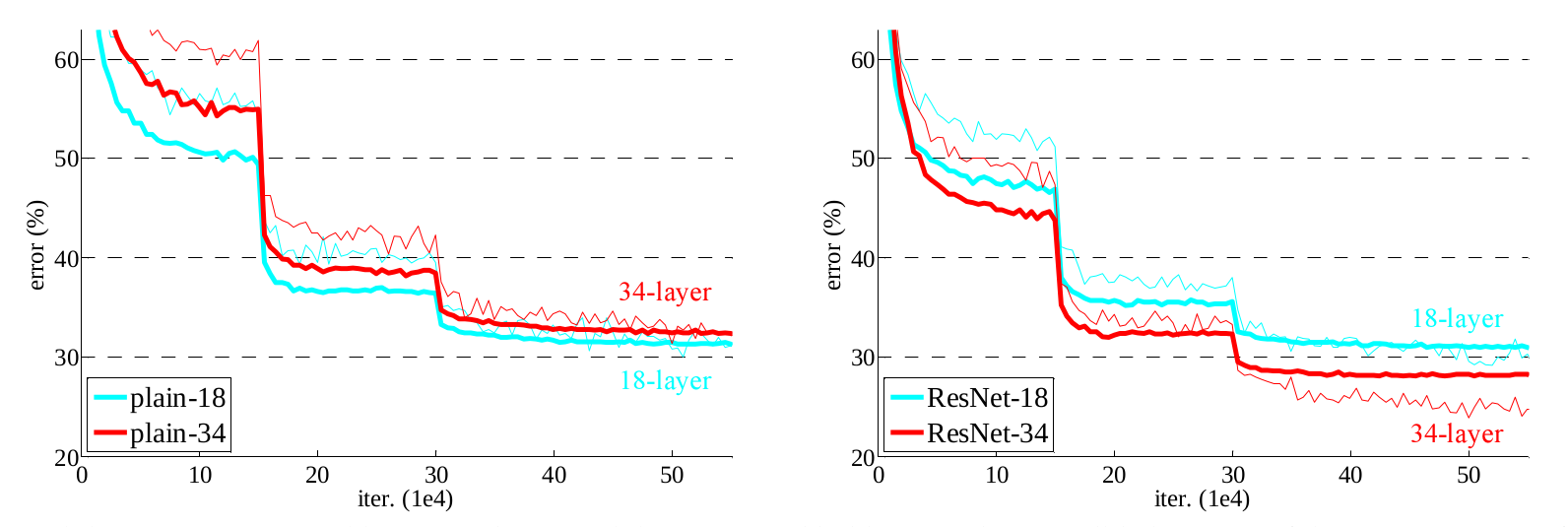
Figure 3

To demonstrate how much better the ResNet are they comapred it with a 34 layer model and a 18 layer model both with plain and residual mappings and the results were not so astounding the 18 layer plain net outperformed the 34 layer plain net and in the case of ResNet the 34 layer ResNet outperformed the 18 layer ResNet as can be seen in figure 3.

ResNet50 Architecture

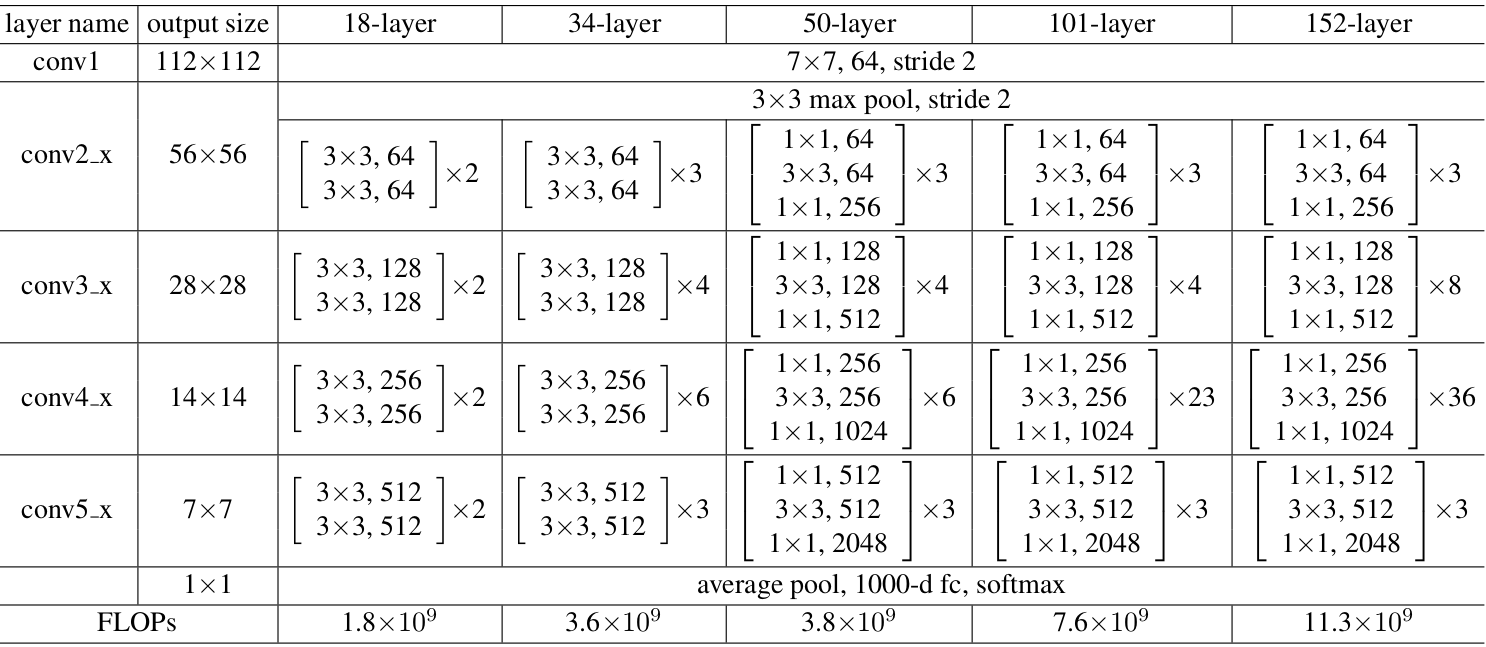
Table 1

Now we are going to discuss about Resnet 50 and also the architecture for the above talked 18 and 34 layer ResNet is also given residual mapping and not shown for simplicity.

There was a small change that was made for the ResNet 50 and above that before this the shortcut connections skipped two layers but now they skip three layers and also there was 1 * 1 convolution layers added that we are going to see in detail with the ResNet 50 Architecture.

So as we can see in the table 1 the resnet 50 architecture contains the following element:

• A convoultion with a kernel size of 7 * 7 and 64 different kernels all with a stride of size 2 giving us 1 layer.
• Next we see max pooling with also a stride size of 2.
• In the next convolution there is a 1 * 1,64 kernel following this a 3 * 3,64 kernel and at last a 1 * 1,256 kernel, These three layers are repeated in total 3 time so giving us 9 layers in this step.
• Next we see kernel of 1 * 1,128 after that a kernel of 3 * 3,128 and at last a kernel of 1 * 1,512 this step was repeated 4 time so giving us 12 layers in this step.
• After that there is a kernal of 1 * 1,256 and two more kernels with 3 * 3,256 and 1 * 1,1024 and this is repeated 6 time giving us a total of 18 layers.
• And then again a 1 * 1,512 kernel with two more of 3 * 3,512 and 1 * 1,2048 and this was repeated 3 times giving us a total of 9 layers.
• After that we do a average pool and end it with a fully connected layer containing 1000 nodes and at the end a softmax function so this gives us 1 layer.

We don't actually count the activation functions and the max/ average pooling layers.

so totaling this it gives us a 1 + 9 + 12 + 18 + 9 + 1 = 50 layers Deep Convolutional network.

Result

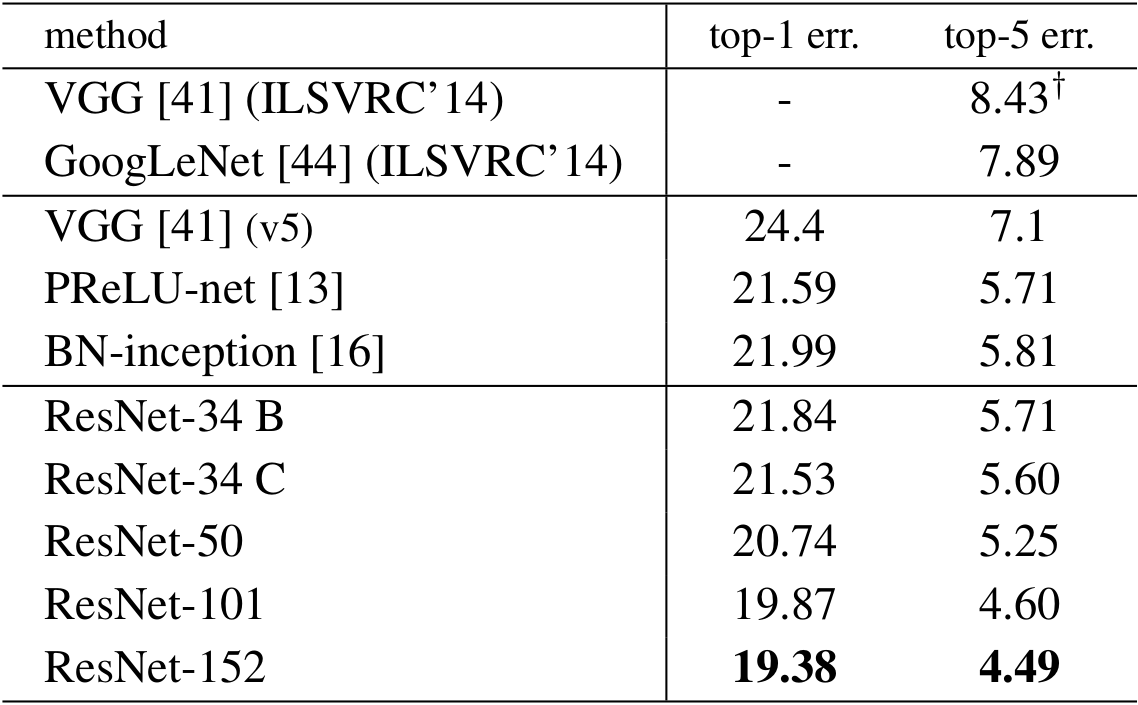
The Result were pretty good on the ImageNet validation set, The ResNet 50 model achieved a top-1 error rate of 20.47 percent and and achieved a top-5 error rate of 5.25 percent, This is reported for single model that consists of 50 layers not a ensemble of it. below is the table given if you want to compare it with other ResNets or with other models.

Uses

• This architecture can be used on computer vision tasks such as image classififcation, object localisation, object detection.
• and this framework can also be applied to non computer vision tasks to give them the benifit of depth and to reduce the computational expense also.

Resources

• Research paper for Deep residual learning.
• VGG-19 by Aakash Kaushik (opengenus).
• Floating point operations per second (FLOPS) of Machine Learning models.
• Convolutional Neural Network by Piyush Mishra and Junaid N Z (OpenGenus)