Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Splay trees are Self adjusting Binary Trees with additional property that recently accessed elements as kept near the top and hence, are quick to access next time. After performing operations, the tree gets adjusted/ modified and this modification of tree is called Splaying.
Why Splaying?
The Frequently accessed elements moves closer to root so that they can be accessed quickly. Having frequently used nodes near the root is useful for implementing cache and garbage collection as the access time is reduced significantly for real-time performance.
Splaying
Whenver a node is accessed, a splaying operation is performed on that node. This is a sequence of operations done on the node which sequentially brings up that node closer to root and eventually makes it as root of that tree. Now, if we want to access that same node from the tree then the time complexity will be O(1). This is what we mean by frequently accessed elements are easily accessible in less time.
Insertion in Splay Tree
Pseudocode
- If root is NULL we allocate a new node and return it as root of the tree.
- Check for insertion location by searching the tree for the parent.
- After finding parent node link the new node with that node and perform Splaying operation which makes new node as root of the tree.
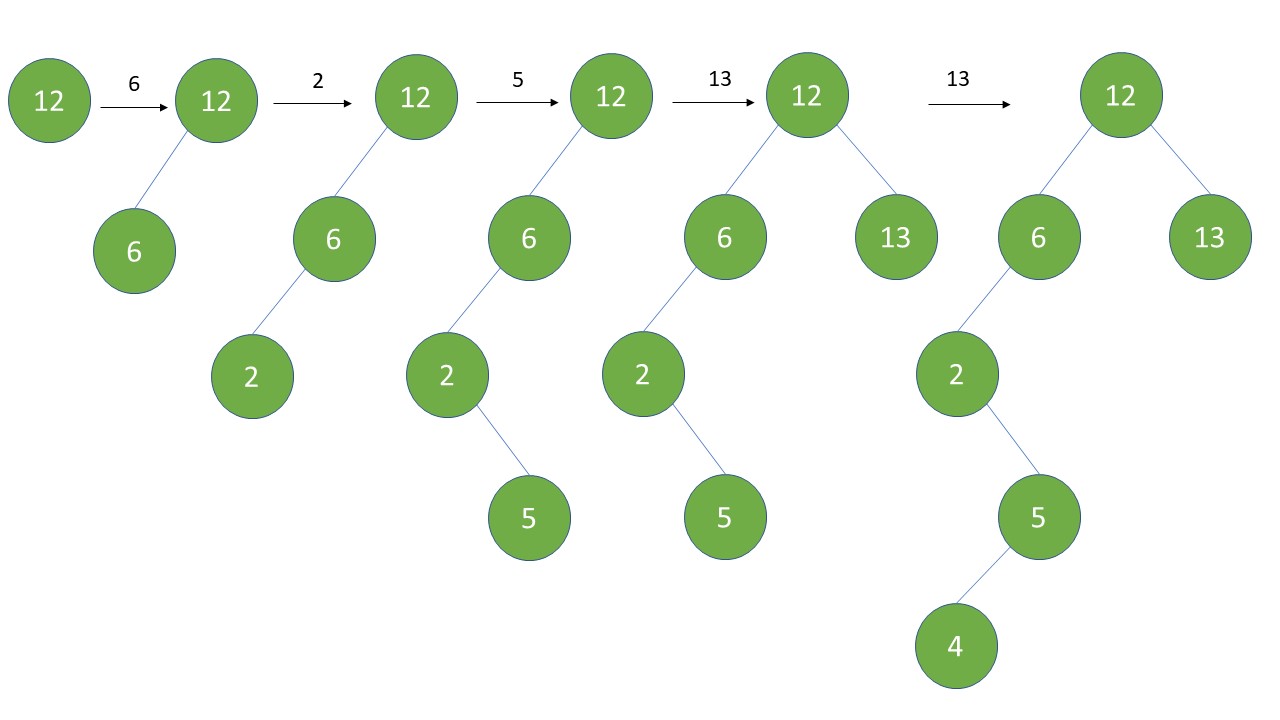
12 -> 6 -> 2 -> 5 -> 13 -> 4
Below Image doesn't include rotation step. This is just simple insertion operation for a BST.
Insert(T,n)
temp = T.root
y = NULL
while temp is not equal to NULL{
y = temp
if n.data < temp.data
temp = temp.left
else temp = temp.right
}
n.parent = y
if y == NULL //Check if Tree is empty. If empty then make n as root of tree.
T.root = n
else if n.data < y.data
y.left = n
else y.right = n
Splay(T,n)
When we call Insert on an empty tree the data is made to be root node of the tree.
Then we call another Insert function, now it will assign temp variable as T.root. and y as NULL.
Checks while loop condition. As new temp variable is not empty, it enters loop.
Assigns y = temp (temp is root now)
Checks if n.data is less than temp.data that is compares the new data with the node in tree. If new data to be inserted is less than the tree node then temp = temp.left
updates temp as its pointer to left child.
If n.data is greater than temp.data update temp as temp.right
Now it will come out of loop because the left or right child pointers to the root node are empty i.e. it falsifies the condition temp != NULL.
Assigns n.parent = y. (y is the updated pointer to the child of temp)
Checking if n.data < y.data. If n is less than y value then assign y.left = n
else y.right = n
Call Splay operation.
We will first define class Node.
class Node:
def __init__(self, data):
self.data = data
self.parent = None
self.left = None
self.right = None
def insert(self, key):
node = Node(key) //This is a class Node used to create new node.
y = None
x = self.root
while x != None:
y = x
if node.data < x.data:
x = x.left
else:
x = x.right
# y is parent of x
node.parent = y
if y == None:
self.root = node
elif node.data < y.data:
y.left = node
else:
y.right = node
# splay the node
self.__splay(node)
Splaying Operation
Let the node to be accessed be x and parent of that node be p. Let grandparent of x be g. (parent of node p)
Depends upon 3 factor:
- If the node x is left child or right child of its parent node p.
- If the parent node p is root node or not.
- If the parent node is left child or right child of its parent node that is grandparent of node x.
Zig step (right rotation)
This step is done when parent node of inserted node is root node of the tree.
Zig-Zig step (double right rotation)
When parentnode of inserted node is not the root node. And if the inserted node is left child of its parent node and that parent node is left child of its parent node then perform zig zig operation.
Similarly Zag Zag operation is performed if the inserted node is the right child of its parent node and that parent node is the right child of its parent node.
ZigZig rotation(right-right)
G P X
/ \ / \ / \
P T4 rightRotate(G) X G rightRotate(P) T1 P
/ \ ============> / \ / \ ============> / \
X T3 T1 T2 T3 T4 T2 G
/ \ / \
T1 T2 T3 T4
ZagZag rotation(left-left rotation)
G P X
/ \ / \ / \
T1 P leftRotate(G) G X leftRotate(P) P T4
/ \ ============> / \ / \ ============> / \
T2 X T1 T2 T3 T4 G T3
/ \ / \
T3 T4 T1 T2
Zig-Zag step (right and left rotation)
Performed if parent node is not the root node and x is right child of its parent and that parent node is left child of its parent node.
If x is root node then there is no need to perform Splay operation.
Zag-Zig (Left Right Case):
G G X
/ \ / \ / \
P T4 leftRotate(P) X T4 rightRotate(G) P G
/ \ ============> / \ ============> / \ / \
T1 X P T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
Zig-Zag (Right Left Case):
G G X
/ \ / \ / \
T1 P rightRotate(P) T1 X leftRotate(P) G P
/ \ =============> / \ ============> / \ / \
X T4 T2 P T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
Example:
100 100 [20]
/ \ / \ \
50 200 50 200 50
/ search(20) / search(20) / \
40 ======> [20] ========> 30 100
/ 1. Zig-Zig \ 2. Zig-Zig \ \
30 at 40 30 at 100 40 200
/ \
[20] 40
Pseudocode
- Enter in while loop if parent of node x is not None.
- Check if grandparent of node is None. This means our node is at 2nd level. If it is at 2nd level then again check if its right child or left child. If its left child perform right rotation or if its right child then perform left rotation.
- Condition to check if both the parent and grandparent of node x exists and are left children of their parent nodes.
(x == x.parent.left and x.parent == x.parent.parent.left)
If true then perform right rotation on grandparent first then parent. This is Zig Zig condition. - Condition to check if both the parent and grandparent of node x exists and are right children of their parent nodes.
(x == x.parent.right and x.parent == x.parent.parent.right)
ZagZag condition. - Check x == x.parent.right and x.parent == x.parent.parent.left this conditions checks if the parent node is right child and this parent node is left child of "its" parent node. First perform left rotation on parent then right rotation on grandparent. (Zig Zag condition)
- Opposite case will be for Zag Zig condition. Perform right rotation on parent node. then left rotation on grandparent.
def __splay(self, x):
while x.parent != None: //performed when node is not root node
if x.parent.parent == None: //Zig or Zag condition
if x == x.parent.left: //Zig condition
# zig rotation
self.__right_rotate(x.parent)
else:
# zag rotation
self.__left_rotate(x.parent)
elif x == x.parent.left and x.parent == x.parent.parent.left: //ZigZig
# zig-zig rotation
self.__right_rotate(x.parent.parent) //rotate grandparent of x to right
self.__right_rotate(x.parent) //then rotate parent node to right
elif x == x.parent.right and x.parent == x.parent.parent.right: //ZagZag
# zag-zag rotation
self.__left_rotate(x.parent.parent)
self.__left_rotate(x.parent)
elif x == x.parent.right and x.parent == x.parent.parent.left: //ZigZag
# zig-zag rotation
self.__left_rotate(x.parent) //rotate parent to left
self.__right_rotate(x.parent) //rotate updated x to right
else:
# zag-zig rotation
self.__right_rotate(x.parent)
self.__left_rotate(x.parent)
Above code performs multiple Zig-Zag or ZigZig operations until the target node does not become a root node.
Right rotation
x y
/ \ Zig (Right Rotation) / \
y T3 – - – - – - – - - -> T1 x
/ \ < - - - - - - - - - / \
T1 T2 Zag (Left Rotation) T2 T3
Observing the rotation we can see that right child of x is now left child of x and y becomes root node.
In right rotation, reverse of the left rotation happens.
Pseudocode:
- Assign left child of x to y.
- Make right child of y as left child of x.
- Check if right child of y is not None. Make T2 as right child of x.
- Check if parent of x is None. Make y as root node.
- Else if x is a right child then make y as right child of x.
6.Else make y as left child of x. - Make x as y's right child.
- Make y as x's parent node.
def __right_rotate(self, x):
y = x.left
x.left = y.right
if y.right != None:
y.right.parent = x
y.parent = x.parent;
if x.parent == None:
self.root = y
elif x == x.parent.right:
x.parent.right = y
else:
x.parent.left = y
y.right = x
x.parent = y
Left rotation(Zag)
Pseudocode:
- Assign right child of x to y.
- Make left child of y as right child of x.
- Check if left child of y is not None. Make T2 as left child of x.
- Check if parent of x is None. Make y as root node.
- Else if x is a left child then make y as left child of x.
6.Else make y as right child of x. - Make x as y's left child.
- Make y as x's parent node.
def __left_rotate(self, x):
y = x.right
x.right = y.left
if y.left != None:
y.left.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
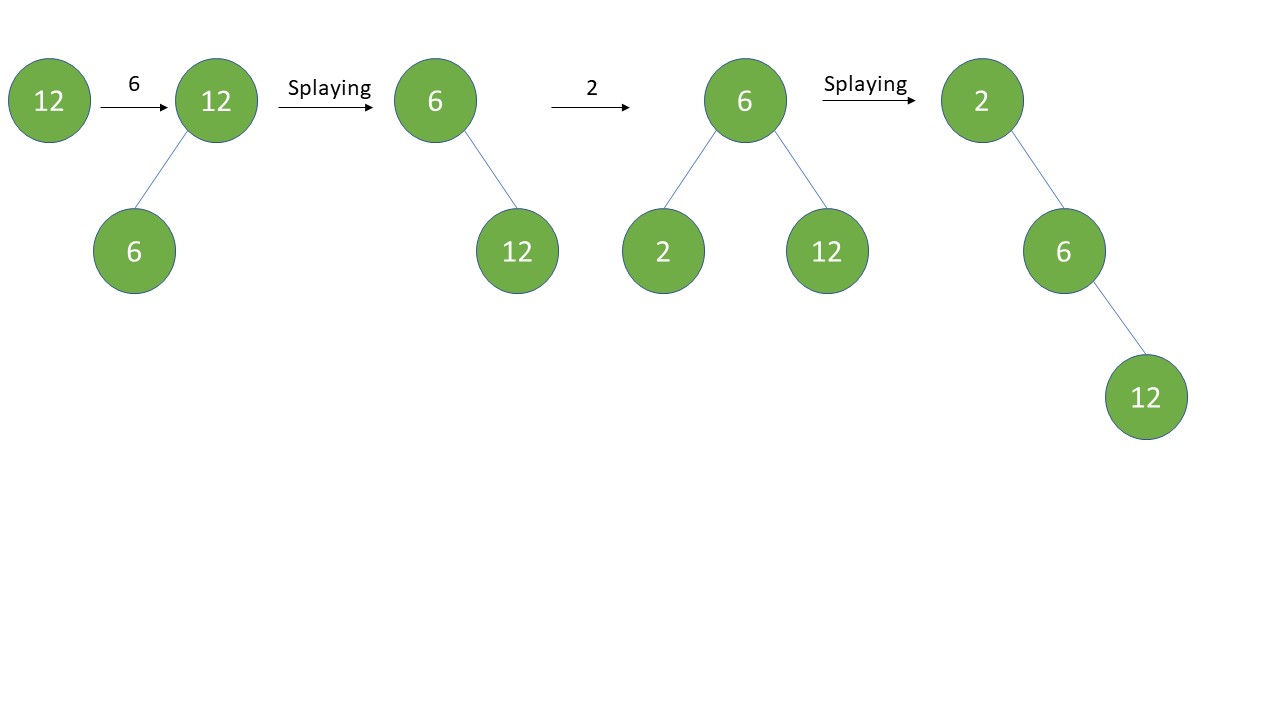
Deletion in Splay Tree
Deletion can be done using Top Down approach.
Let the node to be deleted be x.
First step in deletion is to find the element that has to be deleted in our tree.
Now there could be 2 conditions possible, which are if the key is found and if it is not found.
We will traverse the tree till the key is found, and when it is not found we will eventually reach to the end i.e. leaf node. So, now perform Splay operation and return that key is not found.
Pseudocode
1.Search node to be deleted.
2.Return something if key isnt found.
3.Perform splay operation on that key.
4.Unlink that key node from its parent and its children. causing the tree to split into 2 subtrees.
5.Call Join function.
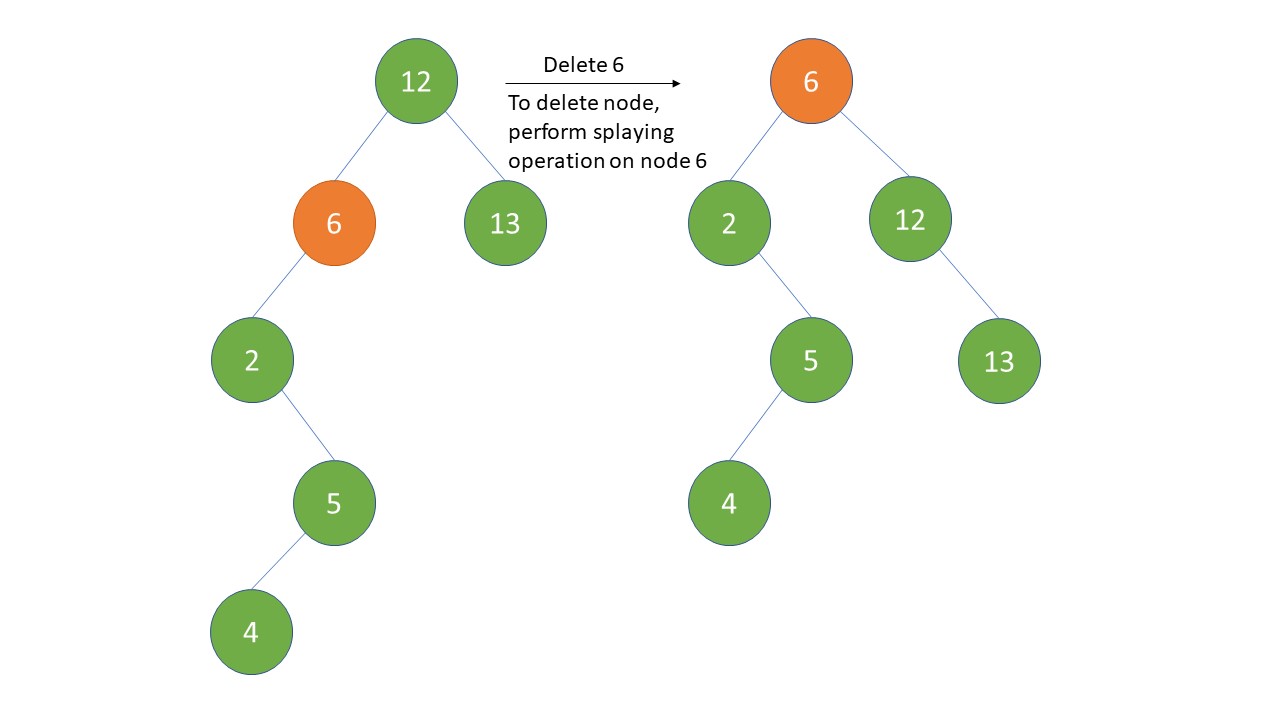
While traversing, if the key is found in the tree then perform Splaying which makes the node as the root of tree as shown in the figure.
Now, the node to be deleted is root of the tree, so split the tree by unlinking the right and left child of x. Now, we will have 2 sub trees.
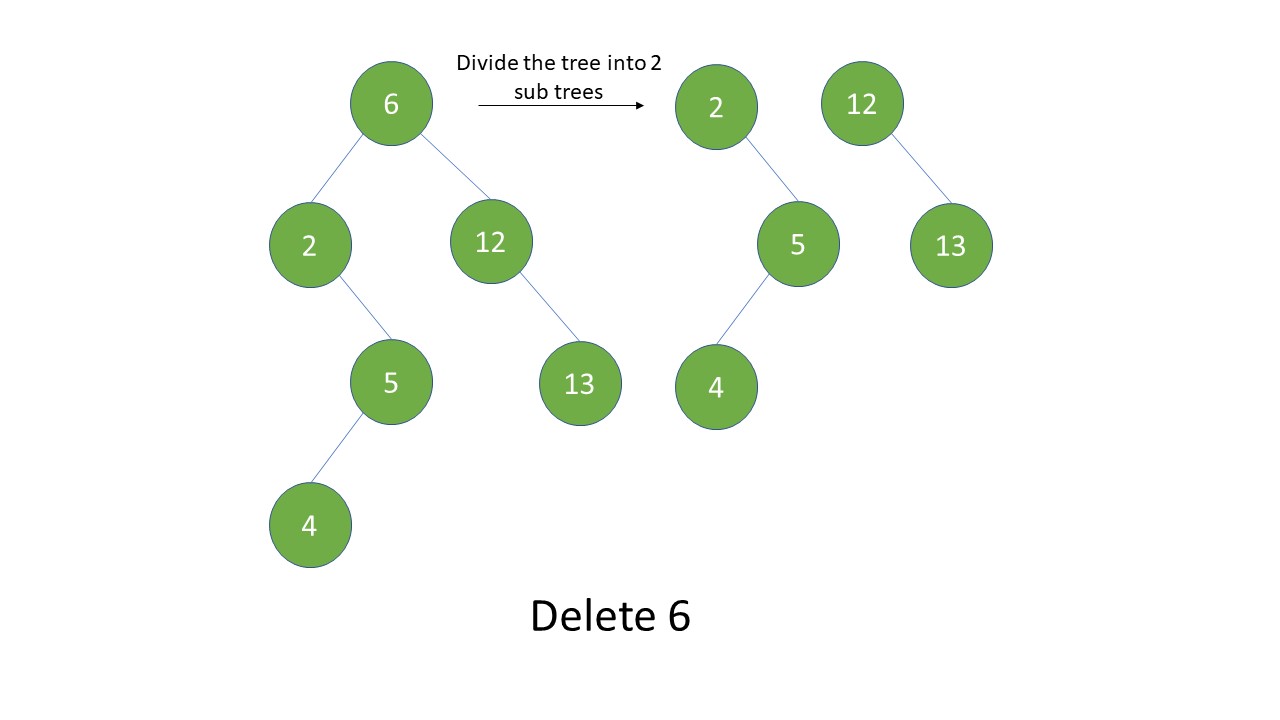
Join the 2 trees using join operation, we will define join operation after deletion operation just to continue with the flow.
Following is the code in python to perform deletion.
def __delete_node_helper(self, node, key):
x = None
t = None
s = None
while node != None: #searching node x to be deleted
if node.data == key:
x = node
if node.data <= key:
node = node.right
else:
node = node.left
if x == None:
#If the node is not found then perform splaying on the recently accessed node
print "Couldn't find key in the tree"
self.__splay(x)
return
# split operation
self.__splay(x) #if the key is found again perform splaying on x
#After splaying x is root node, check if the right child of x is NULL
if x.right != None:
#if root.right is not NULL
#t is temporary variable, assign t as right child of x
t = x.right
t.parent = None #unlinking x from its right child
else: #If right child is empty then t = none
t = None
#3 steps to unlink x from its right child
s = x
s.right = None
x = None
#Now we have 2 trees, so join them
if s.left != None: #Check if left subtree is empty or not
s.left.parent = None #Unlinking parent node 'x' from its left child
self.root = self.__join(s.left, t) #Perform join operation on both trees
s = None
Now let us define join operation
Note that even though the right subtree is empty we have to perform splay operation on the maximum element in left subtree
Join operation is done by finding the maximum value in left subtree, then splaying it.
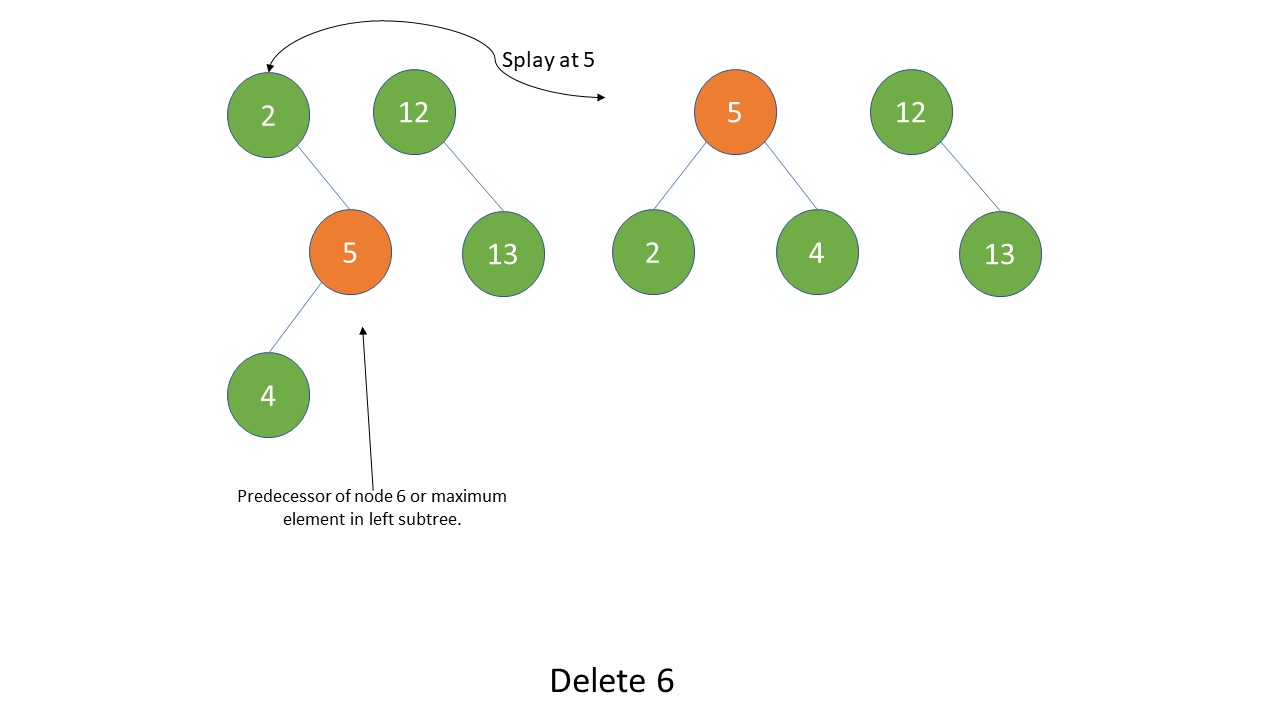
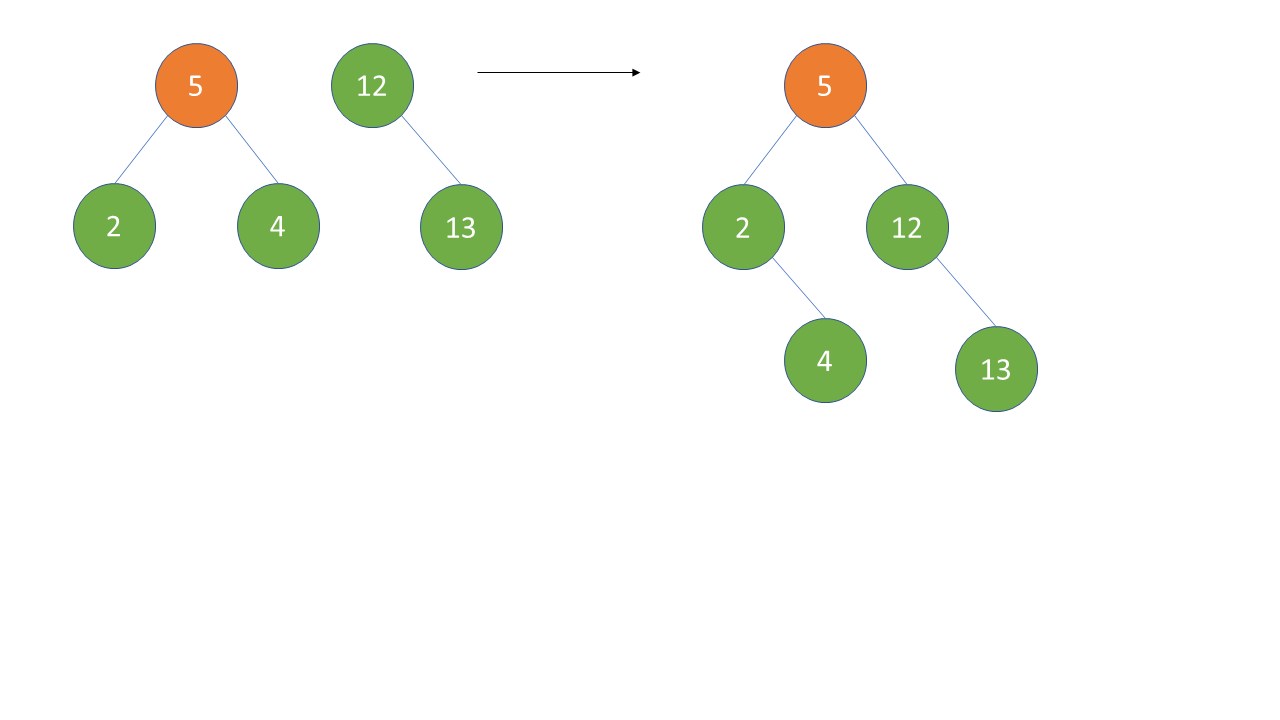
Pseudocode
1.If left subtree is empty then return right subtree as final tree. else perform 3th step.
2.If right subtree is empty then still perform 3th step.
3.Find maximum value node from the left subtree and perform splaying on that maximum node to bring it at the top.
4.Make the root of right subtree as the right child of root of the left subtree.
def __join(self, s, t): #s is left subtree's root, t is right subtree's root
if s == None: #if left subtree is empty
return t #return right subtree as it is.
if t == None: #if right subtree is empty
x = self.maximum(s)
self.__splay(x)
return x
x = self.maximum(s)
self.__splay(x)
#pointing right child of x to t
x.right = t
#making parent of right child as x
t.parent = x
return x
If left subtree is empty then we will simply return right subtree as it is.
Else if right subtree is empty then we will find the latest predecessor of our deleting node key by calling maximum function on left subtree which returns the greatest element from the left subtree. Then perform splaying operation on that element.
Else if both suhbtrees are not empty then find last predecessor of the node to be deleted or find the maximum value node in the left subtree, then splay it to bring that largest node to the top. Then link the root of right subtree as the right child of left subtree's root.
We have called maximum function in our code above. Because of the properties of BST, the implementation of maximum function is very easy, we just have to traverse to the most right child in our left subtree.
Pseudocode:
1.If right child of node is empty return that node.
2.Else if right child is present then call the right child of that node again and again till node.right == None.
def maximum(self, node):
while node.right != None:
node = node.right
return node
To find the greatest element in a Binary search tree we will use its fundamental property that the right subtree of a node contains only nodes with keys greater than the node’s key.
Using recursion we will traverse towards the most rightward key of that tree. We first check if right child of a node is emyty or not. If its not empty then traverse its right child again and again till our condition of node.right != None returns False.
Similarly for minimum function visit the most left node of the tree as the left subtree of a node contains only nodes with keys lesser than the node’s key.
Pseudocode:
1.If left child of node is empty return that node.
2.Else if left child exists then call the left child of that node till we reach leaf node i.e. node.left == None.
def minimum(self, node):
while node.left != None:
node = node.left
return node
Traverse the left subtree till node.left returns None.
Search Operation
Pseudocode
1.Check if node to be find is none or key is equal to root node, then return that node as found.
2.If key to be found is less than node traverse left child recursively till we find the target key and reach leaf node.
3.If key is greater than node then traverse its right child till its found and upto the leaf node.
Calling search function recursively
def __search_tree_helper(self, node, key):
if node == None or key == node.data:
return node
if key < node.data:
return self.__search_tree_helper(node.left, key)
return self.__search_tree_helper(node.right, key)
We will search an element according to the rules of BST. If the key is greater than node traverse its right child recursively, and if key is less than the node then traverse its left child recursively.
InOrder Traversal
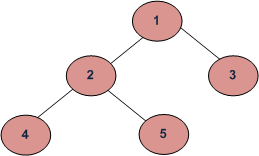
Inorder (Left, Root, Right) : 4 2 5 1 3
Pseudocode:
- Check if root node is None or not.
- If node is not empty then call inorder function again with its left child as argument. It checks again if node exist or not.
- Reach to the lowest level and print that node value if node has no children.
- Move back up (parent), print its value and explore its right subtree.
- Repeat step 4 till we reach root node.
- Start exploring right subtree and repeat from step 2 to 5.
Code:
def __in_order_helper(self, node):
if node != None:
self.__in_order_helper(node.left)
sys.stdout.write(node.data + " ") #print its data and a blankspace
self.__in_order_helper(node.right)
We are recursively traversing the left children of tree until we reach the leaf node then explore its right sibling then its parent node and its right sibling. again the parent node of current node recursively. Then we reach at the root node. We will now explore to the deepest of right subtree and print the leaf nodes values first then their parent repeatedly.
Successor and predcessor of a given node:
Successor
Pseudocode:
- Check if right child of root exists or not.
- If it exists then call minimum function to find minimum value (We have already explained the maximum function).
Successor is the left node of the right subtree of x.
def successor(self, x):
# if the right subtree is not null,
# the successor is the leftmost node in the
# right subtree
if x.right != None:
return self.minimum(x.right)
# else it is the lowest ancestor of x whose
# left child is also an ancestor of x.
y = x.parent
while y != None and x == y.right:
x = y
y = y.parent
return y
To find successor we will traverse its right subtree.
First check if right child exists or not, if it exists then we would want to find a minimum value node. For that we will call its left child in recursion until we reach the leaf node.
Predecessor
Pseudocode
- Check if left child exists or not.
- If it does then call minimum function on left subtree.
(minimum function is already being covered)
Predecessor is the rightmost node in left subtree.
def predecessor(self, x):
# if the left subtree is not null,
# the predecessor is the rightmost node in the
# left subtree
if x.left != None:
return self.maximum(x.left)
y = x.parent
while y != None and x == y.left:
x = y
y = y.parent
return y
Predecessor is the maximum value node in the left subtree.
First check if left child exist or not, if it does then for finding the maximum value in left tree, we will explore the right children of root until we reach the right most node This is a leaf node.
Putting all the functions together:
import sys
class Node:
def __init__(self, data):
self.data = data
self.parent = None
self.left = None
self.right = None
class SplayTree:
def __init__(self):
self.root = None
def __search_tree_helper(self, node, key):
if node == None or key == node.data:
return node
if key < node.data:
return self.__search_tree_helper(node.left, key)
return self.__search_tree_helper(node.right, key)
def __delete_node_helper(self, node, key):
x = None
t = None
s = None
while node != None:
if node.data == key:
x = node
if node.data <= key:
node = node.right
else:
node = node.left
if x == None:
print "Couldn't find key in the tree"
return
# split operation
self.__splay(x)
if x.right != None:
t = x.right
t.parent = None
else:
t = None
s = x
s.right = None
x = None
# join operation
if s.left != None:
s.left.parent = None
self.root = self.__join(s.left, t)
s = None
# rotate left at node x
def __left_rotate(self, x):
y = x.right
x.right = y.left
if y.left != None:
y.left.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
# rotate right at node x
def __right_rotate(self, x):
y = x.left
x.left = y.right
if y.right != None:
y.right.parent = x
y.parent = x.parent;
if x.parent == None:
self.root = y
elif x == x.parent.right:
x.parent.right = y
else:
x.parent.left = y
y.right = x
x.parent = y
# Splaying operation. It moves x to the root of the tree
def __splay(self, x):
while x.parent != None:
if x.parent.parent == None:
if x == x.parent.left:
# zig rotation
self.__right_rotate(x.parent)
else:
# zag rotation
self.__left_rotate(x.parent)
elif x == x.parent.left and x.parent == x.parent.parent.left:
# zig-zig rotation
self.__right_rotate(x.parent.parent)
self.__right_rotate(x.parent)
elif x == x.parent.right and x.parent == x.parent.parent.right:
# zag-zag rotation
self.__left_rotate(x.parent.parent)
self.__left_rotate(x.parent)
elif x == x.parent.right and x.parent == x.parent.parent.left:
# zig-zag rotation
self.__left_rotate(x.parent)
self.__right_rotate(x.parent)
else:
# zag-zig rotation
self.__right_rotate(x.parent)
self.__left_rotate(x.parent)
# joins two trees s and t
def __join(self, s, t):
if s == None:
return t
if t == None:
return s
x = self.maximum(s)
self.__splay(x)
x.right = t
t.parent = x
return x
def __in_order_helper(self, node):
if node != None:
self.__in_order_helper(node.left)
sys.stdout.write(node.data + " ")
self.__in_order_helper(node.right)
# In-Order traversal
# Left Subtree -> Node -> Right Subtree
def inorder(self):
self.__in_order_helper(self.root)
# search the tree for the key k
# and return the corresponding node
def search_tree(self, k):
x = self.__search_tree_helper(self.root, k)
if x != None:
self.__splay(x)
# find the node with the minimum key
def minimum(self, node):
while node.left != None:
node = node.left
return node
# find the node with the maximum key
def maximum(self, node):
while node.right != None:
node = node.right
return node
# find the successor of a given node
def successor(self, x):
# if the right subtree is not null,
# the successor is the leftmost node in the
# right subtree
if x.right != None:
return self.minimum(x.right)
# else it is the lowest ancestor of x whose
# left child is also an ancestor of x.
y = x.parent
while y != None and x == y.right:
x = y
y = y.parent
return y
# find the predecessor of a given node
def predecessor(self, x):
# if the left subtree is not null,
# the predecessor is the rightmost node in the
# left subtree
if x.left != None:
return self.maximum(x.left)
y = x.parent
while y != None and x == y.left:
x = y
y = y.parent
return y
# insert the key to the tree in its appropriate position
def insert(self, key):
node = Node(key)
y = None
x = self.root
while x != None:
y = x
if node.data < x.data:
x = x.left
else:
x = x.right
# y is parent of x
node.parent = y
if y == None:
self.root = node
elif node.data < y.data:
y.left = node
else:
y.right = node
# splay the node
self.__splay(node)
# delete the node from the tree
def delete_node(self, data):
self.__delete_node_helper(self.root, data)
if __name__ == '__main__':
tree = SplayTree()
tree.insert(33)
tree.insert(44)
tree.insert(67)
tree.insert(5)
tree.insert(89)
tree.insert(41)
tree.insert(98)
tree.insert(1)
tree.search_tree(33)
tree.search_tree(44)
tree.delete_node(89)
tree.delete_node(67)
tree.delete_node(41)
tree.delete_node(5)
tree.delete_node(98)
tree.delete_node(1)
tree.delete_node(44)
tree.delete_node(33)
Question
Which of the following property of splay tree is correct?
Question
After the insertion operation, is the resultant tree a splay tee?