Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

In this article, we will begin our discussion by briefly explaining about transitive closure and the Floyd Warshall Algorithm. We will also see the application of Floyd Warshall in determining the transitive closure of a given graph.
What is Transitive Closure of a graph ?
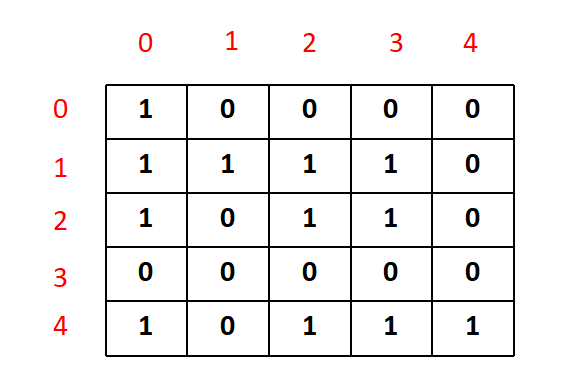
In any Directed Graph, let's consider a node i as a starting point and another node j as ending point. For all (i,j) pairs in a graph, transitive closure matrix is formed by the reachability factor, i.e if j is reachable from i (means there is a path from i to j) then we can put the matrix element as 1 or else if there is no path, then we can put it as 0.
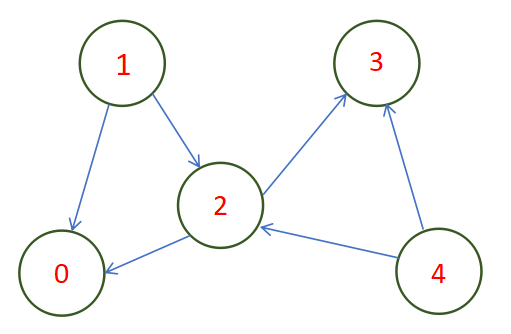
Suppose we are given the following Directed Graph,
Then, the reachability matrix of the graph can be given by,
This matrix is known as the transitive closure matrix, where '1' depicts the availibility of a path from i to j, for each (i,j) in the matrix.
What is Floyd Warshall Algorithm ?
Floyd Warshall Algorithm is used to find the shortest distances between every pair of vertices in a given weighted edge Graph.
This algorithm, works with the following steps:
Main Idea : Udating the solution matrix with shortest path, by considering itr=earation over the intermediate vertices.
- For the first step, the solution matrix is initialized with the input adjacent matrix of the graph. Lets name it as shortest_path
- Next we need to itrate over the number of nodes from {0,1,.....n} one by one by considering them strating vertex. Similarly, another iteration is performed over the nodes {1,2,....,n} by considering ending vertex oen by one.
- For the shortest path, we need to form another iteration which ranges from {1,2,...,k-1}, where vertex k has been picked up as an intermediate vertex.
- For every pair (i, j) of the starting and ending vertices respectively, there are two possible cases.
- if k is an intermediate vertex in the shortest path from i to j, then we check the condition shortest_path[i][j] > shortest_path[i][k] + shortest_path[k][j] and update shortest_path[i][j] accordingly.
- Otherwise if k is not an intermediate vertex, we don't update anything and continue the loop.
A sample demonstration of Floyd Warshall is given below, for a better clarity of the concept.
/// utility function to demonstrate the Floyd Warshall Algorithm
void Floyd_Warshall (int** edges, int num_nodes)
{
int shortest_path[num_nodes][num_nodes];
/// Step -1 - Initializing the adjacent matrix to the solution matrix
for (int i = 0; i < num_nodes; i++)
for (int j = 0; j < num_nodes; j++)
shortest_path[i][j] = edges[i][j];
/// k = intermediate vertex
for (int k = 0; k < num_nodes; k++)
{
/// i = starting vertex
for (int i = 0; i < num_nodes; i++)
{
/// j = ending_vertex
for (int j = 0; j < num_nodes; j++)
{
/// updating the shortest path
if (shortest_path[i][k] + shortest_path[k][j] < shortest_path[i][j])
shortest_path[i][j] = shortest_path[i][k] + shortest_path[k][j];
}
}
}
/// utility function to print the shortest path graph
print_graph(shortest_path);
}
Finding Transitive Closure using Floyd Warshall Algorithm
Well, for finding transitive closure, we don't need to worry about the weighted edges and we only need to see if there is a path from a starting vertex i to an ending vertex j.
The steps involved in this algorithm is similar to the Floyd Warshall method with only one difference of the condition to be checked when there is an intermediate vertex k exits between the starting vertex and the ending vertex.
we need to check two conditions and check if any of them is true,
- Is there a direct edge between the starting vertex and the ending vertex ? If yes, then update the transitive closure matrix value as 1.
- For k, any intermediate vertex, is there any edge between the (starting vertex & k) and (k & ending vertex) ? If yes,then update the transitive closure matrix value as 1.
These conditions are achieved by using or (||) operator along with and(&) operator as shown in the code below.
/// utility function to get back the transitive closure matrix
void transitive_closure(int** edges_list, int num_nodes)
{
/// creating a new 2D array
/// copying the elements from the edges_list array
cout << "Output Transitive Closure Graph:" << endl;
int** output = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
output[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
output[i][j] = edges_list[i][j];
}
}
/*
i = starting node
j = ending node
k = intermediate node, to check if there
is any path from i to j through intermediate nodes
*/
for(int k=0;k<num_nodes;k++)
{
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
/*
output[i][j] = checks if there is direct edge between
the starting vertex and the ending vertex
(output[i][k] && output[k][j]) = if both true then there is
a connected graph, else it's disconnected for certain k in loop
*/
output[i][j] = output[i][j] || (output[i][k] && output[k][j]);
}
}
}
/// function call to print out the transitive closure graph
print_transitive_closure(output,num_nodes);
}
Further we need to print the transitive closure matrix by using another utility function.
Main Code:
#include <iostream>
#include <cmath>
#include <cstdlib>
using namespace std;
/// utility function to print the transitive closure matrix
void print_transitive_closure(int** output, int num_nodes)
{
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << output[i][j] << " ";
}
cout << endl;
}
}
/// utility function to get back the transitive closure matrix
void transitive_closure(int** edges_list, int num_nodes)
{
/// creating a new 2D array
/// copying the elements from the edges_list array
cout << "Output Transitive Closure Graph:" << endl;
int** output = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
output[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
output[i][j] = edges_list[i][j];
}
}
/*
i = starting node
j = ending node
k = intermediate node, to check if there
is any path from i to j through intermediate nodes
*/
for(int k=0;k<num_nodes;k++)
{
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
/*
output[i][j] = checks if there is direct edge between
the starting vertex and the ending vertex
(output[i][k] && output[k][j]) = if both true then there is
a connected graph, else it's disconnected for certain k in loop
*/
output[i][j] = output[i][j] || (output[i][k] && output[k][j]);
}
}
}
/// function call to print out the transitive closure graph
print_transitive_closure(output,num_nodes);
}
int main()
{
/*
num_nodes = number of vertex in the graph
num_edges = number of edges in the graph
*/
int num_nodes,num_edges;
cin >> num_nodes >> num_edges;
/// edges_list = adjacent matrix for Directed Graph
int** edges_list = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
edges_list[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
edges_list[i][j] = 0;
}
}
/// filling up the adjacent matrix using input from the user
for(int i=0;i<num_edges;i++)
{
int first_node,second_node;
cin >> first_node >> second_node;
edges_list[first_node][second_node] = 1;
if(i<num_nodes)
edges_list[i][i]=1;
}
cout << "Input Adjacent Matrix Graph:" << endl;
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << edges_list[i][j] << " ";
}
cout << endl;
}
/// function call to the main algorithm
transitive_closure(edges_list,num_nodes);
return 0;
}
Time and Space Complexity Estimation:
This graph algorithm has a Complexity dependent on the number of vertex V present in the graph. At the beginning of the algorithm we are assigning one two dimensional matrix whose total rows and total columns are equal to number of vertex V each. The space taken by the program increases as V increases. Hence that is dependent on V. So, we have the space complexity of O(V^2).
Similarly we have three loops nested together for the main iteration. Each loop iterates for V number of times and this varies as the input V varies. Hence we have a time complexity of O(V^3).
A Small Intuition to The Algorithm With an Example:
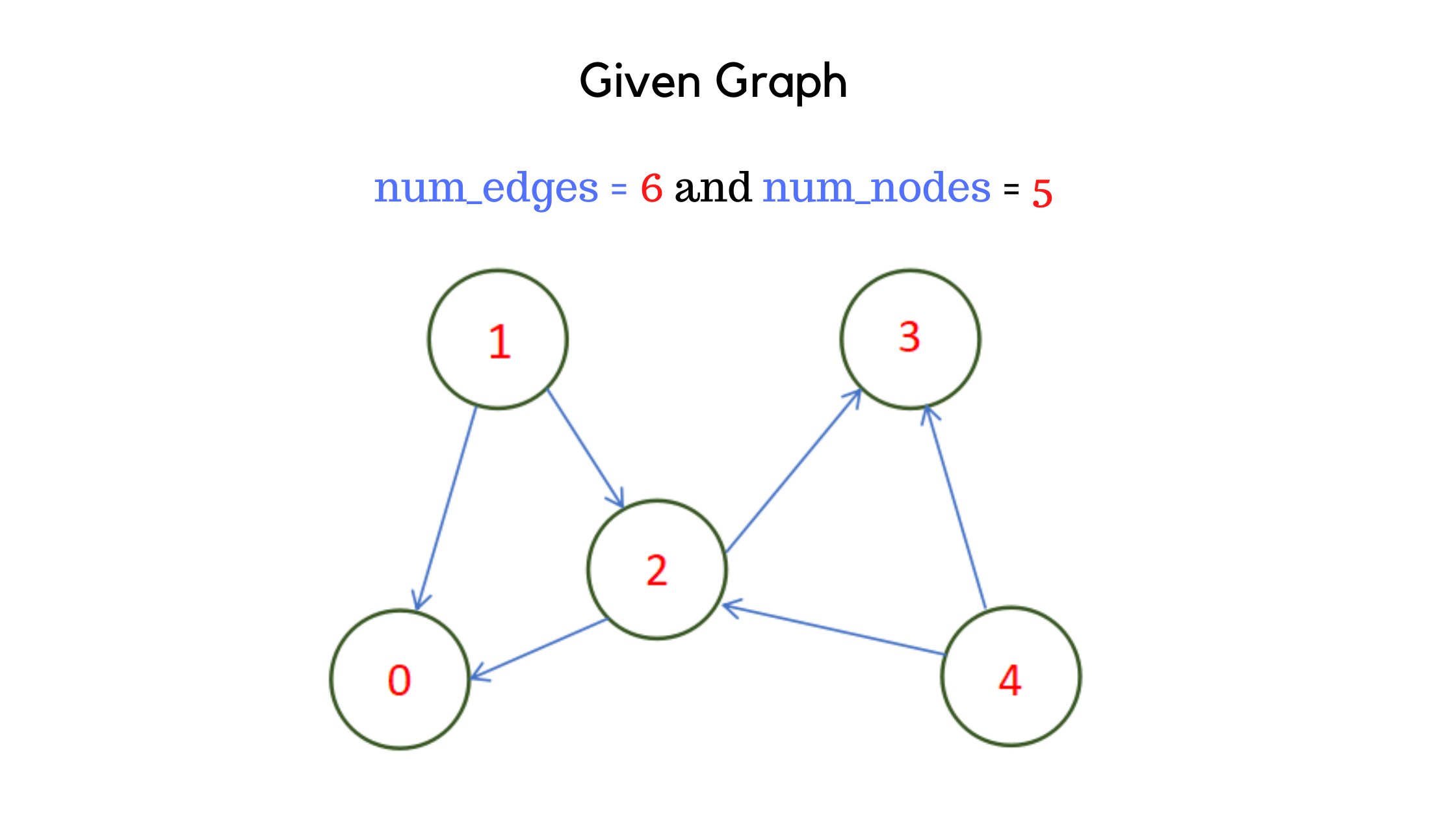
Lets consider the graph we have taken before at the beginning of this article. This graph has 5 nodes and 6 edges in total as shown in the below picture. We have taken the user input in edges_list matrix as explained in the above code.
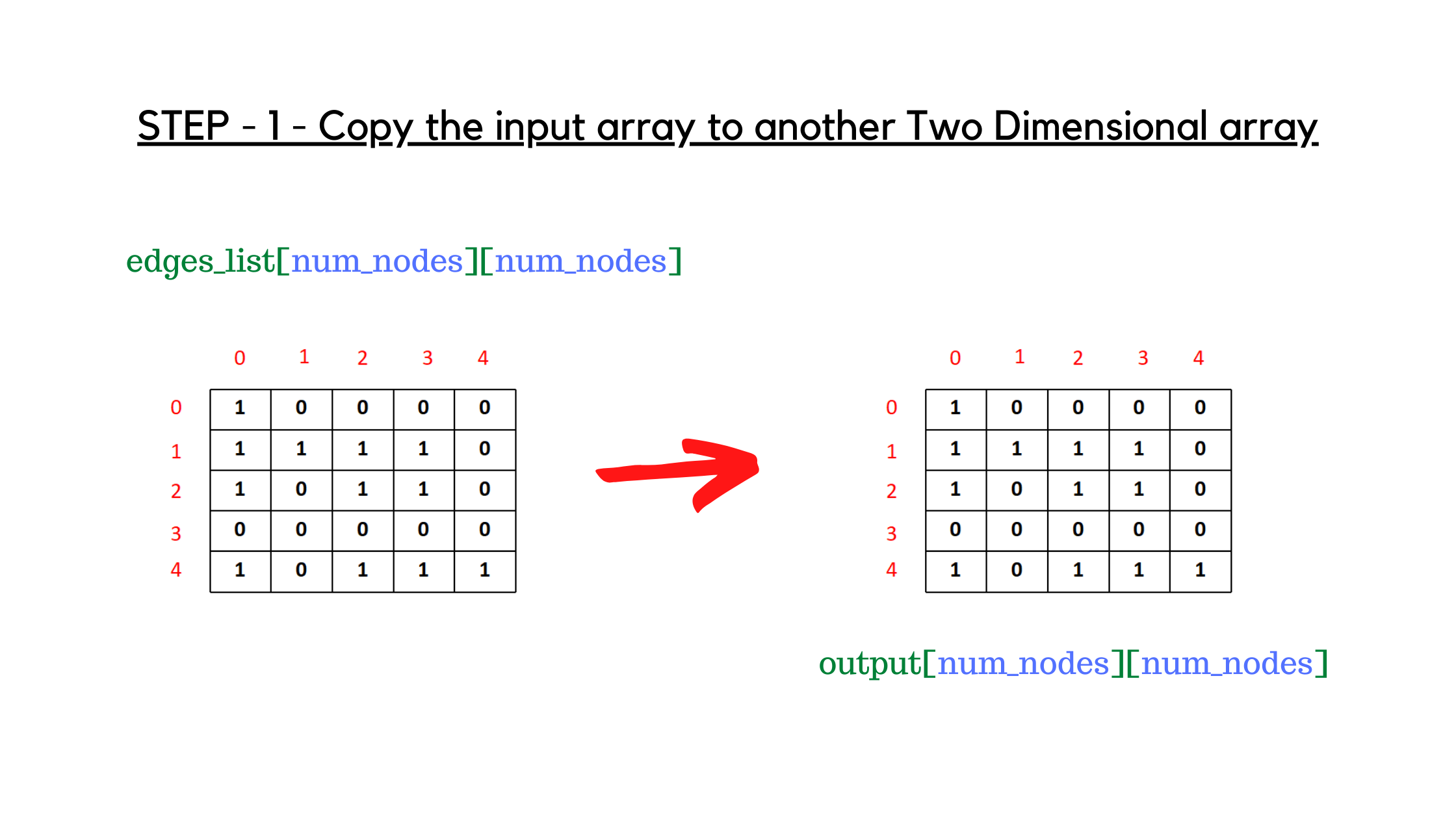
As per the algorithm, the first step is to allocate O(V^2) space as another two dimensional array named output and copy the entries in edges_list to the output matrix. The edges_list matrix and the output matrix are shown below.
Coming to the loop part, the first loop that executes is the innermost one, assigned variable name j to iterate from 0 to num_nodes. This j-loop is inside i-loop , where i ranges from 0 to num_nodes too. And we have an outer loop of k which acts as the intermediate vertex. Let me make it simpler.
While j=1, the value of i=2 and k=0, we interpret it as, i is the starting vertex and j is the ending vertex. First of all we have to check if there is a direct edge from i to j (output[i][j], in the given code) or there is an intermediate edge through k,i.e. to go from starting_node i=2 to ending_node j=1, is there any way through intermediate_node k=0, so that we can determine a path of 2 --- 0 --- 1 (output[i][k] && output[k][j], && is used for logical 'and') ? If any of the two conditions are true, then we have the required path from the starting_vertex to the ending_vertex and we update the value of output[i][j]. accordingly. After all the intermediate vertex ends(i.e outerloop complete iteration) we have the final transitive closure matrix ready.
For a better understading, look at the below attached picture where the major changes occured when k=2.
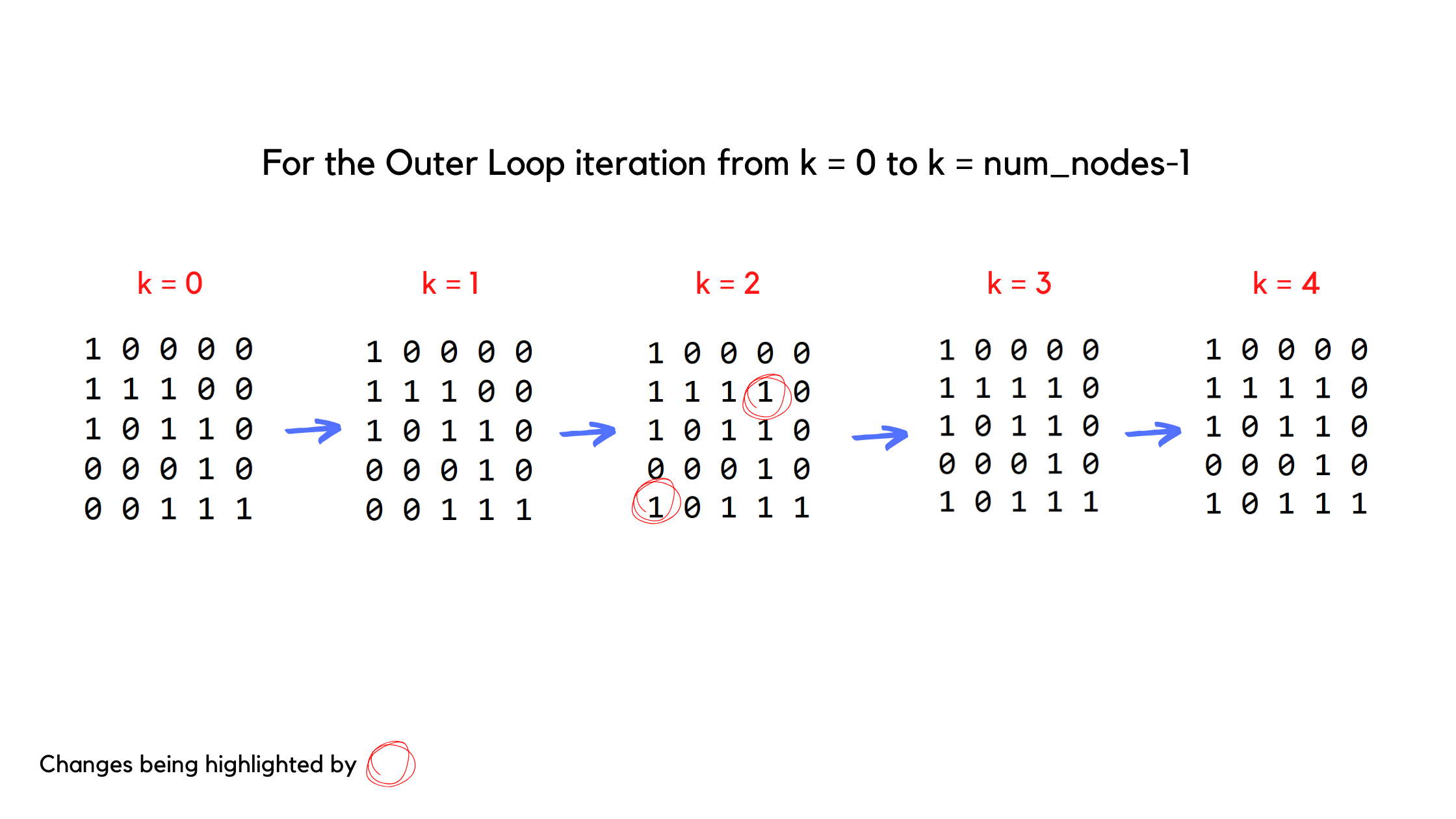
Similarly you can come up with a pen and paper and check manually on how the code works for other iterations of i and j. After the entire loop gets over, we will get the desired transitive closure matrix.
Finally we call the utility function to print the matrix and we are done with our algorithm 😊.
With this article at OpenGenus, you must have the complete idea of finding the Transitive Closure Of A Graph using Floyd Warshall Algorithm. Enjoy.